数学（理）（附加题）卷·2019届天津市静海一中高二上学期期末终结性检测（2018-02）

数学（理）（附加题）卷·2019届天津市静海一中高二上学期期末终结性检测（2018-02）

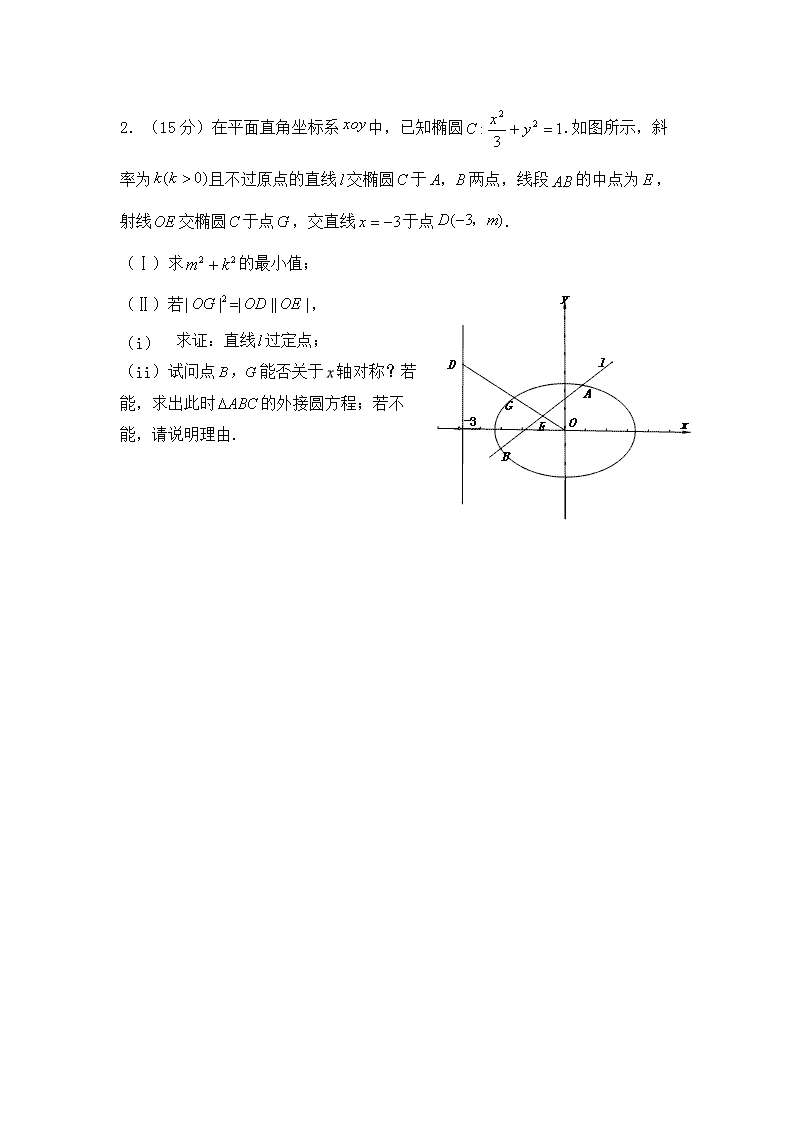
静海一中2017-2018第一学期高二理科数学（附加题）‎ ‎ 期末终结性检测试卷 ‎1．（15分）椭圆中心为坐标原点O,对称轴为坐标轴,且过M（2，） ，N(,1)两点， ‎ ‎（I）求椭圆的方程；‎ ‎（II）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆C恒有两个交点A,B,且？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。‎ ‎2．（15分）在平面直角坐标系中，已知椭圆.如图所示，斜率为且不过原点的直线交椭圆于两点，线段的中点为，射线交椭圆于点，交直线于点.‎ ‎（Ⅰ）求的最小值；‎ ‎（Ⅱ）若，‎ （i） 求证：直线过定点；‎ ‎（ii）试问点能否关于轴对称？若能，求出此时的外接圆方程；若不能，请说明理由. ‎ 小卷1、椭圆过M（2，） ，N(,1)两点，O为坐标原点，‎ ‎（I）求椭圆的方程；‎ ‎（II）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆C恒有两个交点A,B,且？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。‎ 答案：略 ‎2）在平面直角坐标系中，已知椭圆.如图所示，斜率为且不过原点的直线交椭圆于，两点，线段的中点为，射线交椭圆于点，交直线于点.‎ ‎（Ⅰ）求的最小值；（Ⅱ）若∙，（i）求证：直线过定点；‎ ‎（ii）试问点，能否关于轴对称？若能，求出此时的外接圆方程；若不能，请说明理由.‎ ‎【解析】（Ⅰ）由题意:设直线,‎ 由消y得:,设A、B,AB的中点E,则由韦达定理得: =,即,,所以中点E的坐标为E,因为O、E、D三点在同一直线上，所以，即，解得 ‎，所以=,当且仅当时取等号,即的最小值为2.‎ ‎（Ⅱ）（i）证明:由题意知:n>0,因为直线OD的方程为,所以由得交点G的纵坐标为,又因为,,且∙，所以,又由（Ⅰ）知: ,所以解得,所以直线的方程为,即有,令得,y=0,与实数k无关,所以直线过定点(-1,0).‎ ‎（ii）假设点，关于轴对称,则有的外接圆的圆心在x轴上,又在线段AB的中垂线上,‎ 由（i）知点G(,所以点B(,又因为直线过定点(-1,0),所以直线的斜率为，又因为，所以解得或6，又因为,所以舍去,即，此时k=1，m=1，E，AB的中垂线为2x+2y+1=0，圆心坐标为，G(,圆半径为，圆的方程为.综上所述, 点，关于轴对称,此时的外接圆的方程为