- 2023-11-17 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学下册 第27章 圆
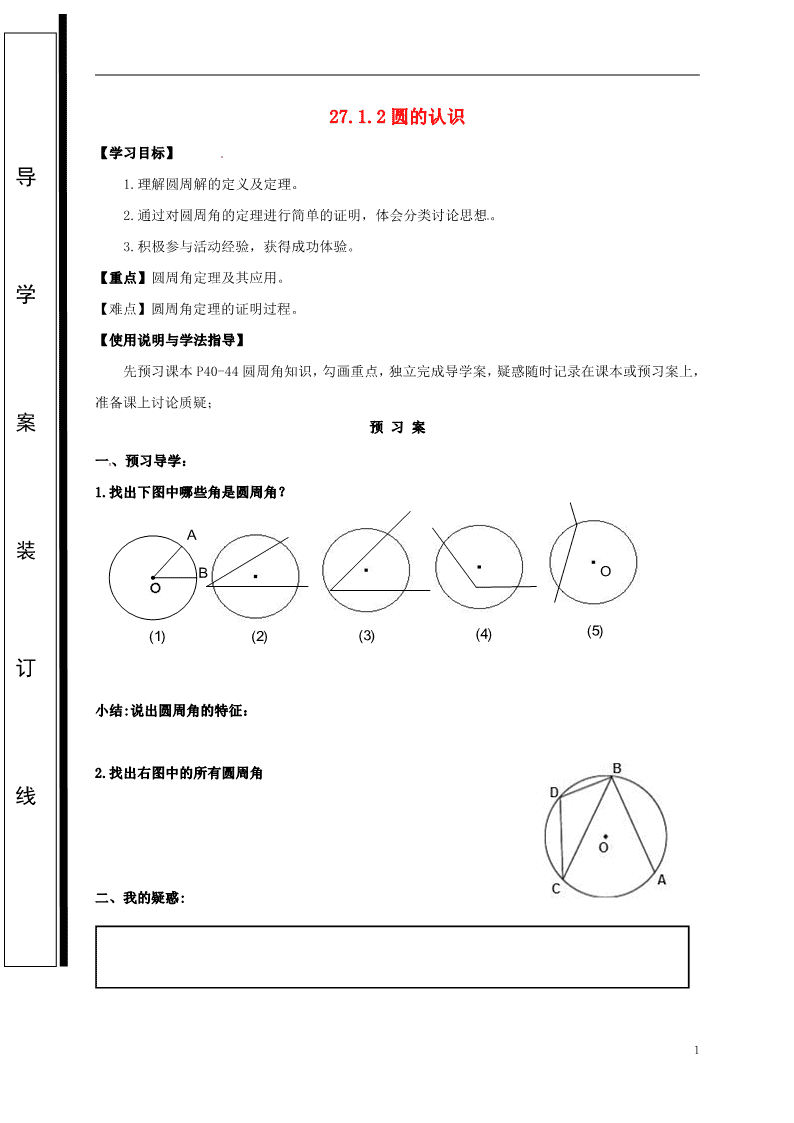
1 27.1.2 圆的认识 【学习目标】 1.理解圆周解的定义及定理。 2.通过对圆周角的定理进行简单的证明,体会分类讨论思想。 3.积极参与活动经验,获得成功体验。 【重点】圆周角定理及其应用。 【难点】圆周角定理的证明过程。 【使用说明与学法指导】 先预习课本 P40-44 圆周角知识,勾画重点,独立完成导学案,疑惑随时记录在课本或预习案上, 准备课上讨论质疑; 预 习 案 一、预习导学: 1.找出下图中哪些角是圆周角? 小结:说出圆周角的特征: 2.找出右图中的所有圆周角 二、我的疑惑: 导 学 案 装 订 线 � (5) � (4) � (3) � (2) � (1) � O � B � A 2 合作探究 探究一:直径所对圆周角的特征 例 1:如图,线段 AB 是⊙O 的直径,点 C 是⊙O 上任意一点(除点 A、B), 那么,∠ACB 就是直 径 AB 所对的圆周角.想想看,∠ACB 会是怎么样的角?为什么呢? 结论:直径所对的圆周角是______________,90°的圆周角所对的弦是________. 探究二:同弧所对的圆周角与圆心角的关系 例 2:如右图所示,∠ADB、∠ACB、∠AOB 分别是什么角? 它们有什么共同点? (1)分别量出 ⌒ AB所对的两个圆周角的度数,比较一下,再 变动点 C 在圆周上的位置,看看圆周角的度数有没有变化,你发现什么规律? (2)分别量出 ⌒ AB所对的圆周角和圆心角的度数,比较下下,你发现了什么? 由此你能猜想出什么结论? 证明你的猜想 (1) 3 (2) (3) 当堂练习 1.如图 1,点 A、B、C 在⊙O 上,∠ACB=20°,则∠AOB 的度数是( ) A.10° B.20° C.40° D.70° 4 2.如图 2,AB 是⊙O 的直径,∠ABC=30°,则∠BAC=( ) A.90° B.60° C.45° D.30° 3.图 3,△ABC 是等边三角形,动点 P 在圆周的劣弧 AB 上,且不与 A、B 重合,则∠BPC 等于( ) A.30° B.60° C.90° D.45° 4.如图 4,点 C 是 的中点,∠OAB=40°,则∠BOC 的度数是( ) A.40° B.50° C.70° D.80° 5.如图 5,已知 AB 是⊙O 的直径,BC 为弦,∠ABC=30°.过圆心 O 作 OD⊥BC 交弧 BC 于点 D,连接 DC,则∠DCB=( ) A.20° B.30° C.40° D.60° 【课堂小结】 1.知识方面: 2.数学思想方法: C A B P查看更多