2011年长春市学业考试数学试题

2011年长春市学业考试数学试题

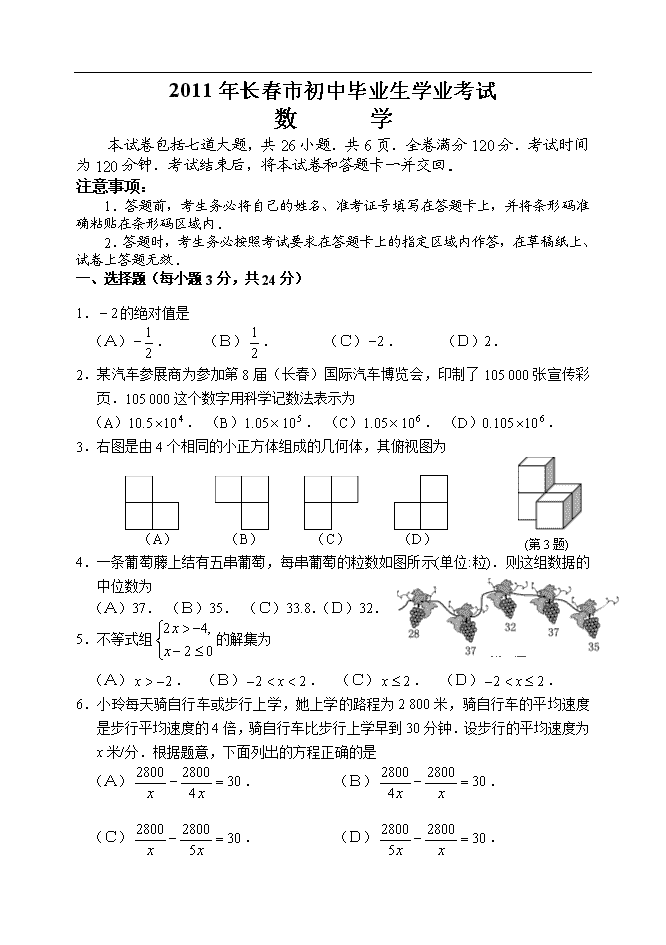
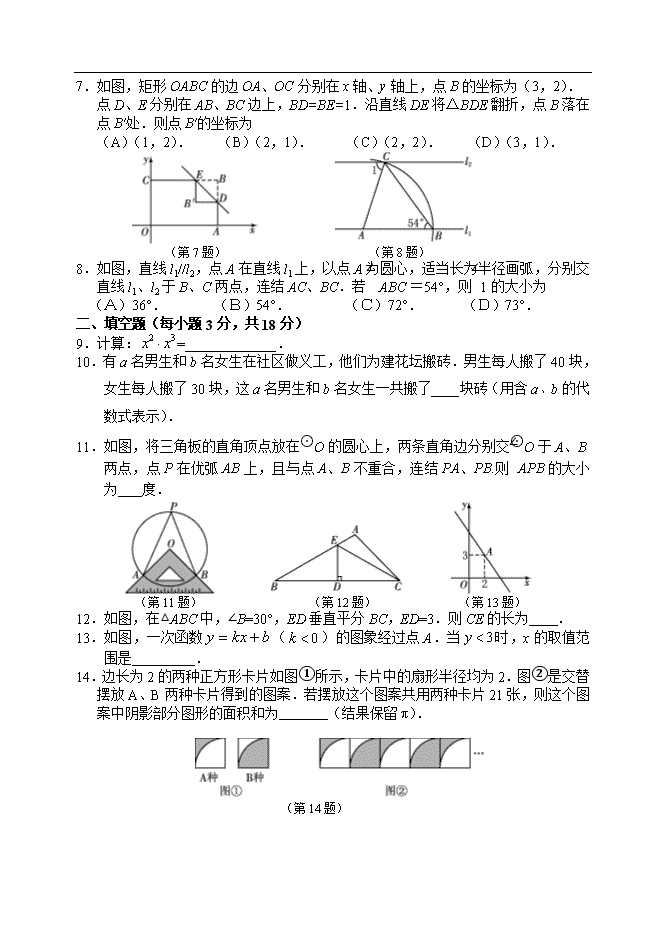
‎2011年长春市初中毕业生学业考试 数 学 本试卷包括七道大题，共26小题．共6页．全卷满分120分．考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回．‎ 注意事项：‎ ‎ 1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．‎ ‎2．答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸上、试卷上答题无效．‎ 一、选择题（每小题3分，共24分）‎ ‎1．的绝对值是 ‎（Ａ）． （Ｂ）． （Ｃ）． （Ｄ）2．‎ ‎2．某汽车参展商为参加第8届（长春）国际汽车博览会，印制了105 000张宣传彩页．105 000这个数字用科学记数法表示为 ‎（A）10.5． （B）1.05． （C）1.05． （D）0.105．‎ ‎3．右图是由4个相同的小正方体组成的几何体，其俯视图为 ‎ ‎ ‎(第3题)‎ ‎（A） （B） （C） （D）‎ ‎（（第4题）‎ ‎4．一条葡萄藤上结有五串葡萄，每串葡萄的粒数如图所示(单位:粒)．则这组数据的中位数为 ‎（Ａ）37． （Ｂ）35． （Ｃ）33.8．（Ｄ）32．‎ ‎5．不等式组的解集为 ‎（Ａ）． （Ｂ）． （Ｃ）． （Ｄ）．‎ ‎6．小玲每天骑自行车或步行上学，她上学的路程为2 ‎800米，骑自行车的平均速度是步行平均速度的4倍，骑自行车比步行上学早到30分钟．设步行的平均速度为x米/分．根据题意，下面列出的方程正确的是 ‎（Ａ）． （Ｂ）．‎ ‎（Ｃ）． （Ｄ）．‎ ‎7．如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（3，2）．‎ 点D、E分别在AB、BC边上，BD=BE=1．沿直线DE将△BDE翻折，点B落在点B′处．则点B′的坐标为 ‎（A）（1，2）． （B）（2，1）． （C）（2，2）． （D）（3，1）．‎ ‎ ‎ ‎（第7题） （第8题）‎ ‎8．如图，直线l1//l2，点A在直线l1上，以点A为圆心，适当长为半径画弧，分别交直线l1、l2于B、C两点，连结AC、BC．若∠＝54°，则∠1的大小为 ‎（Ａ）36°． （Ｂ）54°． （Ｃ）72°． （Ｄ）73°．‎ 二、填空题（每小题3分，共18分）‎ ‎9．计算：=_____________．‎ ‎10．有a名男生和b名女生在社区做义工，他们为建花坛搬砖．男生每人搬了40块，女生每人搬了30块，这a名男生和b名女生一共搬了____块砖（用含a、b的代数式表示）．‎ ‎11．如图，将三角板的直角顶点放在⊙O的圆心上，两条直角边分别交⊙O于A、B两点，点P在优弧AB上，且与点A、B不重合，连结PA、PB.则∠APB的大小为__ _度．‎ ‎ ‎ ‎（第11题） （第12题） （第13题）‎ ‎12．如图，在△ABC中，∠B=30°，ED垂直平分BC，ED=3．则CE的长为 ．‎ ‎13．如图，一次函数（）的图象经过点A．当时，x的取值范围是 ． ‎ ‎14．边长为2的两种正方形卡片如图①所示，卡片中的扇形半径均为2．图②是交替摆放A、B两种卡片得到的图案．若摆放这个图案共用两种卡片21张，则这个图案中阴影部分图形的面积和为 （结果保留π）．‎ ‎（第14题）‎ 三、解答题（每小题5分，共20分）‎ ‎15．先化简，再求值：，其中．‎ ‎16.小华有3张卡片，小明有2张卡片，卡片上的数字如图所示．小华和小明分别从自己的卡片中随机抽取一张．请用画树状图（或列表）的方法，求抽取的两张卡片上的数字和为6的概率．‎ ‎17．在长为‎10m，宽为‎8m的矩形空地上，沿平行于矩形各边的方向分割出三个全等的小矩形花圃，其示意图如图所示．求其中一个小矩形花圃的长和宽．‎ ‎18．平放在地面上的直角三角形铁板ABC的一部分被沙堆掩埋，其示意图如图所示．量得角A为54°，斜边AB的长为‎2.1m，BC边上露出部分BD长为‎0.9m．求铁板BC边被掩埋部分CD的长．（结果精确到‎0.1m）‎ ‎【参考数据：sin54°=0.81，cos54°=0.59，tan54°=1.38】‎ 四、解答题（每小题6分，共12分）‎ ‎19．如图，平面直角坐标系中，直线与x轴交于点A，与双曲线在第一象限内交于点B，BC⊥x轴于点C，OC=2AO．求双曲线的解析式．‎ ‎20．在正方形网格图①、图②中各画一个等腰三角形．每个等腰三角形的一个顶点为格点A，其余顶点从格点B、C、D、E、F、G、H中选取，并且所画的两个三角形不全等．‎ ‎ ‎ 五、解答题（每小题6分，共12分）‎ ‎21．如图，平面直角坐标系中，⊙P与x轴分别交于A、B两点，点P的坐标为（3，－1），AB=．‎ ‎（1）求⊙P的半径．（4分）‎ ‎（2）将⊙P向下平移，求⊙P与x轴相切时平移的距离．（2分）‎ ‎22．某校课外兴趣小组从我市七年级学生中抽取2 000人做了如下问卷调查，将统计结果绘制了如下两幅统计图．‎ 问卷 您平时喝饮料吗？（ ） (A)不喝． (B)喝．‎ 请选择B选项的同学回答下面问题：‎ 请您减少喝饮料的数量，将节省下来的钱捐给希望工程，您愿意平均每月减少多少瓶？（ ） (A)0瓶． (B)1瓶． (C)2瓶． (D)2瓶以上．‎ 根据上述信息解答下列问题：‎ ‎（1）求条形统计图中n的值．（2分）‎ ‎（2）如果每瓶饮料平均3元钱，“少2瓶以上”按少喝3瓶计算．‎ ‎①求这2000名学生一个月少喝饮料能节省多少钱捐给希望工程？（2分）‎ ‎②按上述统计结果估计，我市七年级6万学生一个月少喝饮料大约能节省多少钱捐给希望工程？（2分）‎ 六、解答题（每小题7分，共14分）‎ ‎23．如图，平面直角坐标系中，抛物线交y轴于点A．P为抛物线上一点，且与点A不重合．连结AP，以AO、AP为邻边作□OAPQ，PQ所在直线与x轴交于点B．设点P的横坐标为．‎ ‎（1）点Q落在x轴上时m的值．（3分）‎ ‎（3）若点Q在x轴下方，则为何值时，线段BQ的长取最大值，并求出这个最大值．（4分）‎ ‎【参考公式：二次函数的顶点坐标为（）】‎ ‎24．探究 如图①，在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE，∠FAB=∠EAD=90°，连结AC、EF．在图中找一个与△FAE全等的三角形，并加以证明．（5分）‎ 应用 以□ABCD的四条边为边，在其形外分别作正方形，如图②，连结EF、GH、IJ、KL．若□ABCD的面积为5，则图中阴影部分四个三角形的面积和为 ．（2分）‎ ‎ ‎ 七、解答题（每小题10分，共20分）‎ ‎25．甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量(件)与时间(时)的函数图象如图所示．‎ ‎（1）求甲组加工零件的数量y与时间之间的函数关系式．（2分）‎ ‎（2）求乙组加工零件总量的值．（3分）‎ ‎（3）甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？再经过多长时间恰好装满第2箱？（5分）‎ ‎26．如图，∠C=90°，点A、B在∠C的两边上，CA=30，CB=20，连结AB．点P从点B出发，以每秒4个单位长度的速度沿BC方向运动，到点C停止．当点P与B、C两点不重合时，作PD⊥BC交AB于D，作DE⊥AC于E．F为射线CB上一点，且∠CEF=∠ABC．设点P的运动时间为x（秒）．‎ ‎（1）用含有x的代数式表示CF的长．（2分）‎ ‎（2）求点F与点B重合时x的值．（2分）‎ ‎（3）当点F在线段CB上时，设四边形DECP与四边形DEFB重叠部分图形的面积为y（平方单位）．求y与x之间的函数关系式．（3分）‎ ‎（4）当x为某个值时，沿PD将以D、E、F、B为顶点的四边形剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的x值．（3分）‎