- 2023-04-27 发布 |
- 37.5 KB |
- 16页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2011年全国各地100份中考数学试卷分类汇编第28--图形的相似与位似
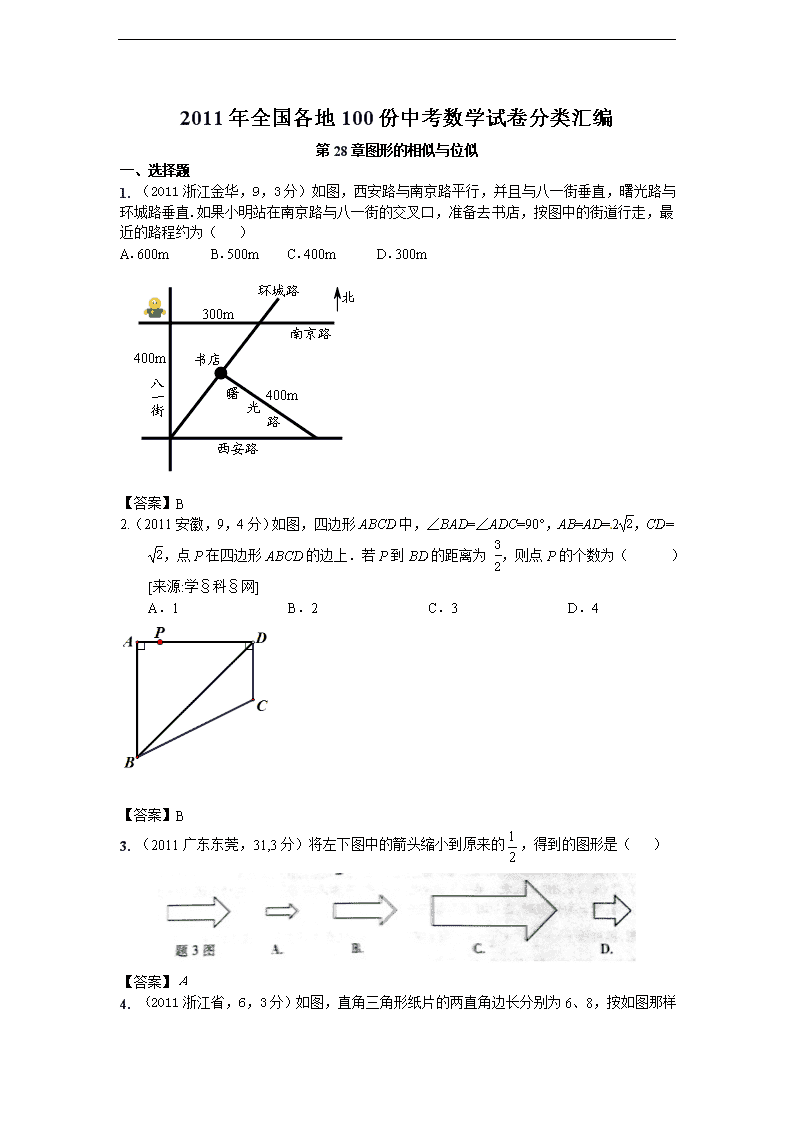
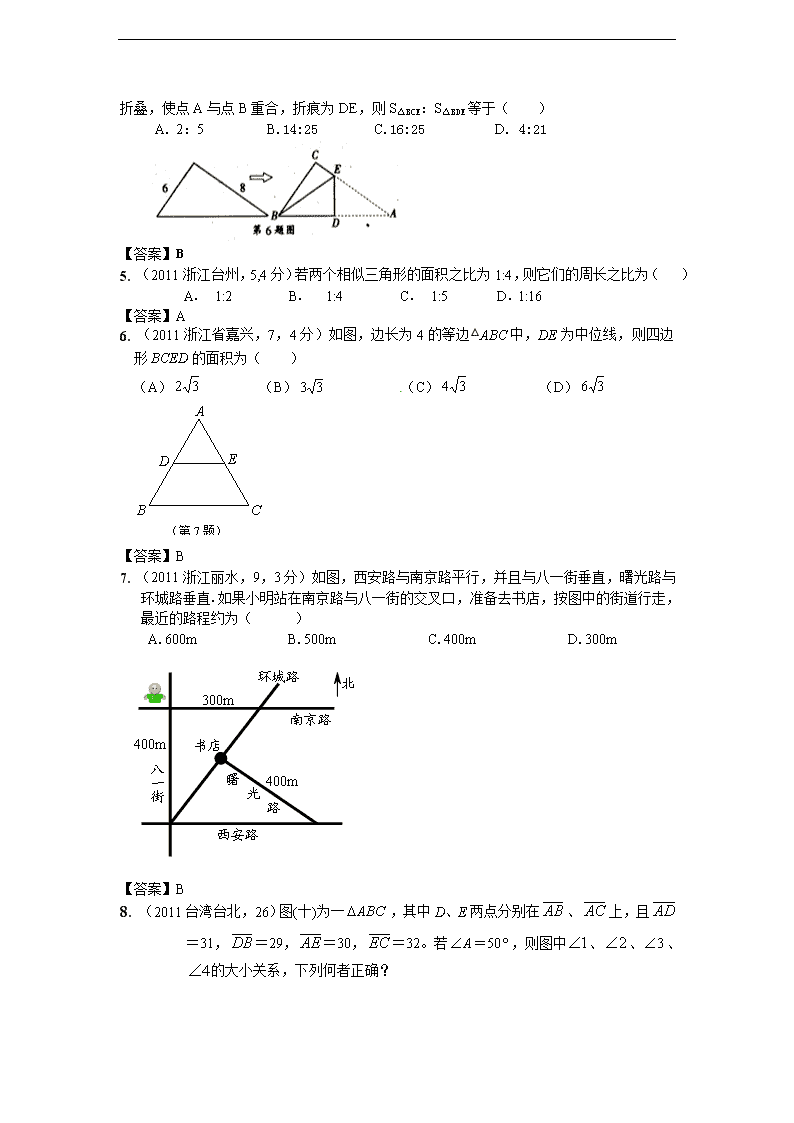
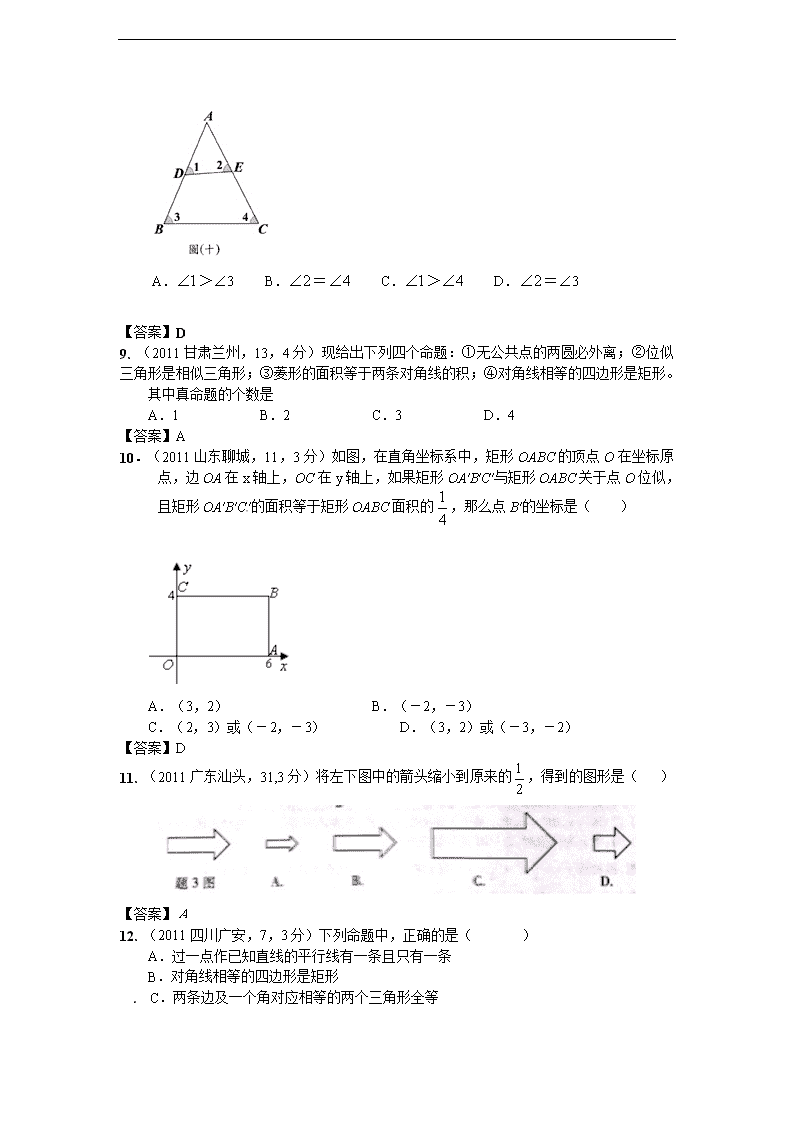
2011 年全国各地 100 份中考数学试卷分类汇编 第 28 章图形的相似与位似 一、选择题 1. (2011 浙江金华,9,3 分)如图,西安路与南京路平行,并且与八一街垂直,曙光路与 环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最 近的路程约为( ) A.600m B.500m C.400m D.300m 【答案】B 2.(2011 安徽,9,4 分)如图,四边形 ABCD 中,∠BAD=∠ADC=90°,AB=AD=2 2,CD= 2, 点 P 在四边形 ABCD 的边上.若 P 到 BD 的距离为 3 2 ,则点 P 的个数为( )[来 源:学§科§网] A.1 B.2 C.3 D.4 【答案】B 3. (2011 广东东莞,31,3 分)将左下图中的箭头缩小到原来的 1 2 ,得到的图形是( ) 【答案】A 4. (2011 浙江省,6,3 分)如图,直角三角形纸片的两直角边长分别为 6、8,按如图那样 折叠,使点 A 与点 B 重合,折痕为 DE,则 S△BCE:S△BDE 等于( ) A. 2:5 B.14:25 C.16:25 D. 4:21 【答案】B 5.(2011 浙江台州,5,4 分)若两个相似三角形的面积之比为 1:4,则它们的周长之比为( ) A. 1:2 B. 1:4 C. 1:5 D. 1:16 【答案】A 6. (2011 浙江省嘉兴,7,4 分)如图,边长为 4 的等边△ABC 中,DE 为中位线,则四边 形 BCED 的面积为( ) (A) 32 (B) 33 (C) 34 (D) 36 (第 7 题) A B C D E 【答案】B 7. (2011 浙江丽水,9,3 分)如图,西安路与南京路平行,并且与八一街垂直,曙光路与 环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走, 最近的路程约为( ) A.600m B.500m C.400m D.300m 【答案】B 8. (2011 台湾台北,26)图(十)为一 ABC ,其中 D、E 两点分别在 AB 、 AC 上,且 AD =31, DB =29, AE =30, EC =32。若 50=A ,则图中 1 、 2 、 3 、 4 的大小关系,下列何者正确? A. 1 > 3 B. 2 = 4 C. 1 > 4 D. 2 = 3 【答案】D 9. (2011 甘肃兰州,13,4 分)现给出下列四个命题:①无公共点的两圆必外离;②位似 三角形是相似三角形;③菱形的面积等于两条对角线的积;④对角线相等的四边形是矩形。 其中真命题的个数是 A.1 B.2 C.3 D.4 【答案】A 10.(2011 山东聊城,11,3 分)如图,在直角坐标系中,矩形 OABC 的顶点 O 在坐标原 点,边 OA 在 x 轴上,OC 在 y 轴上,如果矩形 OA′B′C′与矩形 OABC 关于点 O 位似, 且矩形 OA′B′C′的面积等于矩形 OABC 面积的 1 4 ,那么点 B′的坐标是( ) A.(3,2) B.(-2,-3) C.(2,3)或(-2,-3) D.(3,2)或(-3,-2) 【答案】D 11. (2011 广东汕头,31,3 分)将左下图中的箭头缩小到原来的 1 2 ,得到的图形是( ) 【答案】A 12. (2011 四川广安,7,3 分)下列命题中,正确的是( ) A.过一点作已知直线的平行线有一条且只有一条 B.对角线相等的四边形是矩形 C.两条边及一个角对应相等的两个三角形全等 D.位似图形一定是相似图形 【答案】D 13. ( 2011 重庆江津, 8,4 分)已知如图(1)、(2)中各有两个三角形,其边长和角的度数 已在图上标注,图(2)中 AB、CD 交于 O 点,对于各图中的两个的两个三角形而言,下列说法正 确的是( ) A.都相似 B.都不相似 C.只有(1)相似 D.只有(2)相似 【答案】A· 14. (2011 重庆綦江,4,4 分)若相似△ABC 与△DEF 的相似比为 1 :3,则△ABC 与△DEF 的面积比为( ) A.1 :3 B.1 :9 C.3 :1 D. 1 : 3 【答案】:B 15. (2011 山东泰安,15 ,3 分)如图,点 F 是□ABCD 的边 CD 上一点,直线 BF 交 AD 的延长线于点 E,则下列结论错误..的是 A.ED EA=DF AB B.DE BC=EF FB C. BC DE=BF BE D.BF BE=BC AE 【答案】C 16. (2011 山东潍坊,3,3 分)如图,△ABC 中,BC = 2,DE 是它的中位线,下面三个结 论:⑴DE=1;⑵△ADE∽△ABC;⑶△ADE 的面积与△ABC 的面积之比为 1 : 4。其 中正确的有( ) A . 0 个 B.1 个 C . 2 个 D.3 个 35° 75° 75° 70° (1) A BC D O 4 3 68 (2) 第8题图 【答案】D 17. (2011 湖南怀化,6,3 分)如图 3 所示:△ABC 中,DE∥BC,AD=5,BD=10,AE=3, 则 CE 的值为 A.9 B.6 C.3 D.4 【答案】B 18. (2011 江苏无锡,7,3 分)如图,四边形 ABCD 的对角线 AC、BD 相交于 O,且将这 个四边形分成①、②、③、④四个三角形.若 OA∶OC = OB∶OD,则下 列结论中一定正确的是 ( ) A.①和②相似 B.①和③相似 C.①和④相似 D.②和④相似 A B C DO ① ② ⊙ ③ ⊙ ④ ⊙ (第 7 题) 【答案】B 19. (2011 广东肇庆,5,3 分)如图,已知直线 a∥b∥c,直线 m、n 与 a、b、c 分别交于 点 A、C、E、B、D、F,AC = 4,CE = 6,BD = 3,则 BF = a b c A B C D E F m n A. 7 B. 7.5 C. 8 D. 8.5[来源:学科网] 【答案】B 20.(2011 湖南永州,12,3 分)下列说法正确的是( ) A.等腰梯形的对角线互相平分. B.一组对边平行,另一组对边相等的四边形是平行四边形. C.线段的垂直平分线上的点到线段两个端点的距离相等. D.两边对应成比例且有一个角对应相等的两个三角形相似. 【答案】C 21. (2011 山东东营,11,3 分)如图,△ABC 中,A,B 两个顶点在 x 轴的上方,点 C 的 坐标是(-1,0).以点 C 为位似中心,在 x轴的下方作△ABC 的位似图形△A′B′C,并把△ABC 的边长放大到原来的 2 倍.设点 B 的对应点 B′的横坐标是 a,则点 B 的横坐标是( ) A. 1 2 a B. 1 ( 1)2 a C. 1 ( 1)2 a D. 1 ( 3)2 a B′ A′第 11 题 -1 x 1 O -1 1 y B A C 【答案】D 22. (2011 重庆市潼南,5,4 分)若△ABC~△DEF,它们的面积比为 4:1,则△ABC 与△ DEF 的相似比为 A.2:1 B.1 :2 C.4:1 D.1:4 【答案】A 23. (2011 广东中山,3,3 分)将左下图中的箭头缩小到原来的 1 2 ,得到的图形是( ) 【答案】A 24. (20 11 湖北荆州,7,3 分)如图,P 为线段 AB 上一点,AD 与 BC 交于 E,∠CPD= ∠A=∠B,BC 交 PD 于 F,AD 交 PC 于 G,则图中相似三角形有 A.1 对 B.2 对 C.3 对 D.4 对 第 7 题图 【答案】C 25. 26. 二、填空题 1. (2011 广东广州市,14,3 分)如图 3,以点 O 为位似中心,将五边形 ABCDE 放大后 得到五边形 A′B′C′D′E′,已知 OA=10cm,OA′=20cm,则五边形 ABCDE 的周长与五边形 A′B′C′D′E′的周长的比值是 . 图 3 O A B C D E A′ B′ C′ D′ E′ 【答案】1 2 2. (2011 四川重庆,12,4 分)如图,△ABC 中,DE∥BC,DE 分别交边 AB、AC 于 D、 E 两点,若 AD:AB=1:3,则△ADE 与△ABC 的面积比为 . 【答案】1:9 3. (2011 江苏苏州,17,3 分)如图,已知△ABC 的面积是 3 的等边三角形,△ABC∽△ADE, AB=2AD,∠BAD=45°,AC 与 DE 相交于点 F,则△AEF 的面积等于__________(结果保留 根号). 【答案】 4 33 4. 5. 6. 三、解答题 1. (2011 江西,25,10 分)某数学兴趣小组开展了一次活动,过程如下: 设∠BAC= (0°< <90°).现把小棒依次摆放在两射线 AB,AC 之间,并使小棒两端分 别落在两射线上. 活动一: 如图甲所示,从点 A1 开始,依次向右摆放小棒,使小棒与小棒在两端点处互相垂直,A1A2 为第 1 根小棒. 数学思考: (1)小棒能无限摆下去吗?答: .(填“能”或“不能”) (2)设 AA1=A1A2=A2A3=1. ① = 度; ②若记小棒 A2n-1A2n 的长度为 an(n 为正整数,如 A1A2=a1,A3A4=a2,),求此时 a2,a3 的值, 并直接写出 an(用含 n 的式子表示). 活动二: 如图乙所示,从点 A1 开始,用等长的小棒依次向右摆放,其中 A1A2 为第 1 根小棒,且 A1A2= AA1. 数学思考: (3)若已经向右摆放了 3 根小棒,则 1 = , 2 = , 3 = ;(用 含 的式子表示) (4)若只能..摆放 4 根小棒,求 的范围. 【答案】 【答案】解:(1)能 (2)①22.5° ②方法一: ∵AA1=A1A2=A2A3=1, A1A2⊥A2A3,∴A1A3= 2 ,AA3=1+ 2 . 又∵A2A3⊥A3A4,∴A1A2∥A3A4.同理:A3A4∥A5A6,∴∠A=∠AA2A1=∠AA4A3=∠AA6A5, ∴AA3=A3A4,AA5=A5A6,∴a2= A3A4=AA3=1+ 2 ,a3=AA3+A3A5=a2+A3A5.∵A3A5= 2 a2, ∴a3=A5A6=AA5=a2+ 2 a2=( 2 +1)2. 方法二: ∵AA1=A1A2=A2A3=1, A1A2⊥A2A3,∴A1A3= 2 ,AA3=1+ 2 .[来源:学_科_网 Z_X_X_K] 又∵A2A3⊥A3A4,∴A1A2∥A3A4.同理:A3A4∥A5A6,∴∠A=∠AA2A1=∠AA4A3=∠AA6A5, ∴a2=A3A4=AA3=1+ 2 ,又∵∠A2A3A4=∠A4A5A6=90°,∠A2A4A3=∠A4A6A5,∴△A2A3A4∽△A4A5A6, ∴ 3 2 2 1 a a a ,∴a3= 1 2 2a =( 2 +1)2. an=( 2 +1)n-1. (3) 432 321 ,, (4)由题意得 905 906 ,∴15°< ≤18°. 2. (2011 江苏宿迁,28,12 分)如图,在 Rt△ABC 中,∠B=90°,AB=1,BC= 2 1 ,以点 C 为圆心,CB 为半径的弧交 CA 于点 D;以点 A 为圆心,AD 为半径的弧交 AB 于点 E. (1)求 AE 的长度; (2)分别以点 A、E 为圆心,AB 长为半径画弧,两弧交于点 F(F 与 C 在 AB 两侧), 连接 AF、EF,设 EF 交弧 DE 所在的圆于点 G,连接 AG,试猜想∠EAG 的大小,并说 明理由.� G � F � E � D � C � B � A (第 28 题) 【答案】 解:(1)在 Rt△ABC 中,由 AB=1,BC= 2 1 得 AC= 22 )2 1(1 = 2 5 ∵BC=CD,AE=AD ∴AE=AC-AD= 2 15 . (2)∠EAG=36°,理由如下: ∵FA=FE=AB=1,AE= 2 15 ∴ FA AE = 2 15 ∴△FAE 是黄金三角形 ∴∠F=36°,∠AEF=72° ∵AE=AG,FA=FE ∴∠FAE=∠FEA=∠AGE ∴△AEG∽△FEA ∴∠EAG=∠F=36°. 3. (2011 广东汕头,21,9 分)如图(1),△ABC 与△EFD 为等腰直角三角形,AC 与 DE 重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD 绕点 A 顺时针旋转, 当 DF 边与 AB 边重合时,旋转中止.不考虑旋转开始和结束时重合的情况,设 DE、DF(或 它们的延长线)分别交 BC(或它的延长线)于 G、H 点,如图(2).[来源:学§科§网 Z§ X§X§K] (1)问:始终与△AGC 相似的三角形有 及 ;[来源:学科网] (2)设 CG=x,BH=y,求 y 关于 x 的函数关系式(只要求根据 2 的情况说明理由); (3)问:当 x 为何值时,△AGH 是等腰三角形? 【解】(1)△HGA 及△HAB; (2)由(1)可知△AGC∽△HAB ∴ CG AC AB BH ,即 9 9 x y , 所以, 81y x (3)当 CG< 1 2 BC 时,∠GAC=∠H<∠HAC,∴AC<CH ∵AG<AC,∴AG<GH 又 AH>AG,AH>GH 此时,△AGH 不可能是等腰三角形; 当 CG= 1 2 BC 时,G 为 BC 的中点,H 与 C 重合,△AGH 是等腰三角形; 此时,GC= 9 22 ,即 x= 9 22 当 CG> 1 2 BC 时,由(1)可知△AGC∽△HGA 所以,若△AGH 必是等腰三角形,只可能存在 AG=AH 若 AG=AH,则 AC=CG,此时 x=9 综上,当 x=9 或 9 22 时,△AGH 是等腰三角形. 4. (2011 湖南怀化,21,10 分)如图 8,△ABC,是一张锐角三角形的硬纸片,AD 是边 BC 上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长 HG 是宽 HE 的 2 倍的矩形 EFGH, 使它的一边 EF 在 BC 上,顶点 G、H 分别在 AC,AB 上,AD 与 HG 的交点为 M. (1) 求证: ;AM HG AD BC (2) 求这个矩形 EFGH 的周长. 【答案】 (1) 解:∵四边形 EFGH 为矩形 ∴EF∥GH ∴∠AHG=∠ABC 又∵∠HAG=∠BAC ∴ △AHG∽△ABC ∴ ;AM HG AD BC (2)由(1)得 ;AM HG AD BC 设 HE=x,则 HG=2x,AM=AD-DM=AD-HE=30-x 可得 40 2 30 30 xx ,解得,x=12 , 2x=24 所以矩形 EFGH 的周长为 2×(12+24)=72cm. 5. (2011 上海,25,14 分)在 Rt△ABC 中,∠ACB=90°,BC=30,AB=50.点 P 是 AB 边上任意一点,直线 PE⊥AB,与边 AC 或 BC 相交于 E.点 M 在线段 AP 上,点 N 在线段 BP 上,EM=EN,sin∠EMP= 12 13 . (1)如图 1,当点 E 与点 C 重合时,求 CM 的长; (2)如图 2,当点 E 在边 AC 上时,点 E 不与点 A、C 重合,设 AP=x,BN=y,求 y 关 于 x 的函数关系式,并写出函数的定义域;[来源:Zxxk.Com] (3)若△AME∽△ENB(△AME 的顶点 A、M、E 分别与△ENB 的顶点 E、N、B 对应), 求 AP 的长. 图 1 图 2 备用图 【答案】(1)∵∠ACB=90°,∴AC= 2 2AB BC = 2 250 30 =40. ∵S= 1 2 AB CP = 1 2 AC BC , ∴CP= AC BC AB = 40 30 50 =24. 在 Rt△CPM 中,∵sin∠EMP=12 13 ,[来源:学。科。网 Z。X。X。K] ∴ 12 13 CP CM . ∴CM= 13 12 CP = 13 2412 =26. (2)由△APE∽△ACB,得 PE AP BC AC ,即 30 40 PE x ,∴PE= 3 4 x . 在 Rt△MPE 中,∵sin∠EMP=12 13 ,∴ 12 13 PE ME . ∴EM= 13 12 PE = 13 3 12 4 x = 13 16 x .[来源:Zxxk.Com] ∴PM=PN= 2 2ME PE = 2 213 3 16 4x x = 5 16 x . ∵AP+PN+NB=50,∴x+ 5 16 x +y =50. ∴y = 21 5016 x (0 < x < 32). (3) 第三问:由于给出对应顶点,那么解法一可以直接运用相似和三角比求出对应边长再列 比例式求解。本题还可以通过角度之间的关系转换求解,个人认为从角度入手更加简洁直观 方法如下: ①当点 E 在线段 AC 上时, △AME∽△ENB, AM ME EN NB .∵EM=EN,∴ 2EM AM NB .设 AP=x,由(2)知 EM= 13 16 x ,AM= x PM = 5 11 16 16x x x ,NB= 21 5016 x . ∴ 213 11 21( 50)16 16 16x x x 解得 x1=22,x2=0(舍去). 即 AP=22. ② 当点 E 在线段 BC 上时, 根据外角定理,△ACE∽△EPM,∴ 12 5 AC EP CE MP .∴CE= 5 12 AC = 50 3 .设 AP=x, 易得 BE= 5 (50 )3 x ,∴CE=30 5 (50 )3 x .∴30 5 (50 )3 x = 50 3 .解得 x=42.即 AP=42. ∴AP 的长为 22 或 42. 6. (2011 四川绵阳 25,14) 已知△ABC 是等腰直角三角形,∠A=90°,D 是腰 AC 上的一个动点,过 C 作 CE 垂直于 BD 或 BD 的延长线,垂足为 E,如图 1. (1)若 BD 是 AC 的中线,如图 2,求BD CE 的值; (2)若 BD 是∠ABC 的角平分线,如图 3,求BD CE 的值; (3)结合(1)、(2),请你推断BD CE 的值的取值范围(直接写出结论,不必证明),并探究BD CE 的 值能小于4 3 吗?若能,求出满足条件的 D 点的位置;若不能,请说明理由. 【答案】(1)设AD=x,则AB=2x,根据勾股定理,可得BD= 5x,∵△ABD∽△CDE, BD AB CE CD , 可得 CE= 2 5 x,所以BD CE=5 2 (2)设 AD=x,根据角平分线定理,可知 DC= 2x,AB= 2x+x,由 勾 股 定 理 可 知 BD= (4+2 2)x² △ ABD ∽ △ CDE , 1 2 1 AB EC AD DE , ∴ EC= 2 2 2 x , BD CE=2, (3)由前面两步的结论可以看出, 1BD CE ≥ ,所以这样的点是存在的,D 在 AC 边的五等分点和 点 A 之间 7. (2011 湖北武汉市,24,10 分)(本题满分 10 分) (1)如图 1,在△ABC 中,点 D,E,Q 分别在 AB,AC,BC 上,且 DE∥BC,AQ 交 DE 于点 P.求证: QC PE BQ DP . (2) 如图,在△ABC 中,∠BAC=90°,正方形 DEFG 的四个顶点在△ABC 的边上,连接 AG,AF 分别交 DE 于 M,N 两点.[来源:学科网 ZXXK] ①如图 2,若 AB=AC=1,直接写出 MN 的长; ②如图 3,求证 MN2=DM·EN. 【答案】(1)证明:在△ABQ 中,由于 DP∥BQ, ∴△ADP∽△ABQ, ∴DP/BQ=AP/AQ. 同理在△ACQ 中,EP/CQ=AP/AQ. ∴DP/BQ=EP/CQ. (2) 9 2 . (3)证明:∵∠B+∠C=90°,∠CEF+∠C=90°. ∴∠B=∠CEF, 又∵∠BGD=∠EFC, ∴△BGD∽△EFC. ∴DG/CF=BG/EF, ∴DG·EF=CF·BG 又∵DG=GF=EF,∴GF2=CF·BG 由(1)得 DM/BG=MN/GF=EN/CF∴(MN/GF)2=(DM/BG)·(EN/CF) ∴MN2=DM·EN 8. (2011 河北,20,8 分)如图 10,在 6×8 网格图中,每个小正方形边长均为 1,点 O 和 △ABC 的顶点均在小正方形的顶点. (1)以 O 为位似中心,在网格图中作△A′B′C′和△ABC 位似,且位似比为 1︰2; (2)连接(1)中的 AA′,求四边形 AA′C′C 的周长.(结果保留根号) 【答案】(1)如下图.[来源:学.科.网] (2)四边形 AA′C′C 的周长=4+6 2 9. 10. 11. 12.查看更多