中考数学数与式复习教案

中考数学数与式复习教案

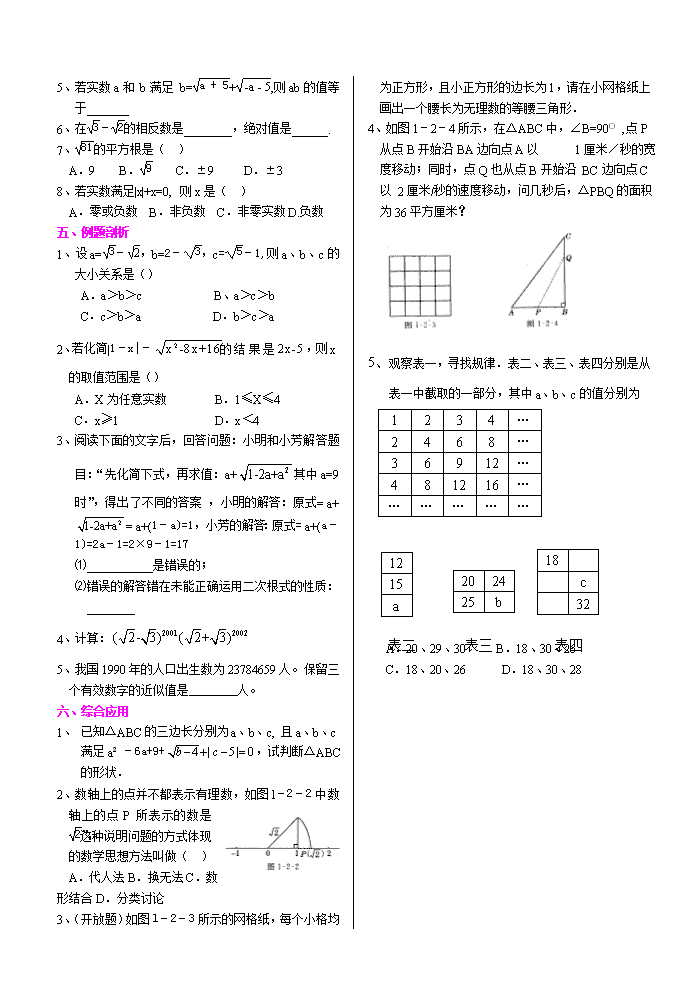
第一篇 数与式 专题一 实数 一、中考要求：‎ ‎1．在经历数系扩张、探求实数性质及其运算规律的过程；从事借助计算器探索数学规律的活动中，发展同学们的抽象概括能力，并在活动中进一步发展独立思考、合作交流的意识和能力．‎ ‎2．结合具体情境，理解估算的意义，掌握估算的方法，发展数感和估算能力．‎ ‎3．了解平方根、立方根、实数及其相关概念；会用根号表示并会求数的平方根、立方根；能进行有关实数的简单四则运算．‎ ‎4．能运用实数的运算解决简单的实际问题，提高应用意识，发展解决问题的能力，从中体会数学的应用价值．‎ 二、中考热点：‎ 本章多考查平方根、立方根、二次根式的有关运算以及实数的有关概念，另外还有一类新情境下的探索性、开放性问题也是本章的热点考题．‎ 三、考点扫描 ‎1、实数的分类：‎ 实数 ‎2、实数和数轴上的点是一一对应的．‎ ‎3、相反数：只有符号不同的两个数互为相反数．‎ ‎ 若a、b互为相反数，则a+b=0， （a、b≠0）‎ ‎4、绝对值：从数轴上看，一个数的绝对值就是表示这个数的点与原点的距离 ‎5、近似数和有效数字；‎ ‎6、科学记数法；‎ ‎7、整指数幂的运算：‎ ‎ （a≠0） ‎ 负整指数幂的性质：‎ ‎ 零整指数幂的性质： （a≠0）‎ ‎8、实数的开方运算：‎ ‎9、实数的混合运算顺序 ‎*10、无理数的错误认识：⑴无限小数就是无理数如1．414141···(41 无限循环）；（2）带根号的数是无理数如；（3）两个无理数的和、差、积、商也还是无理数，如都是无理数，但它们的积却是有理数；（4）无理数是无限不循环小数，所以无法在数轴上表示出来，这种说法错误，每一个无理数在数轴上都有一个唯一位置，如，我们可以用几何作图的方法在数轴上把它找出来，其他的无理数也是如此．‎ ‎*11、实数的大小比较：‎ ‎ (1).数形结合法 ‎(2).作差法比较 ‎(3).作商法比较 ‎(4).倒数法: 如 ‎(5).平方法 四、考点训练 ‎1、（2005、杭州，3分）有下列说法：①有理数和数轴上的点—一对应；②不带根号的数一定是有理数；③负数没有立方根；④－是17的平方根，其中正确的有（ ）‎ ‎ A．0个 B．1个 C．2个 D．3个 ‎2、如果那么x取值范围是（）‎ ‎ A、x ≤2 B. x ＜2 C. x ≥2 D. x＞2‎ ‎3、－8的立方根与的平方根的和为（ ）‎ ‎ A．2 B．0 C．2或一4 D．0或－4‎ ‎4、若2m－4与3m－1是同一个数的平方根，则m为（ ） ‎ ‎ A．－3 B．1 C．－3或1 D．－1‎ ‎5、若实数a和 b满足 b=+,则ab的值等于_______‎ ‎6、在－的相反数是________，绝对值是______.‎ ‎7、的平方根是（ ）‎ ‎ A．9 B． C．±9 D．±3‎ ‎8、若实数满足|x|+x=0, 则x是（ ）‎ ‎ A．零或负数 B．非负数 C．非零实数D.负数 五、例题剖析 ‎1、设a=－，b=2－，c=－1,则a、b、c的大小关系是（）‎ A．a＞b＞c B、a＞c＞b ‎ C．c＞b＞a D．b＞c＞a ‎2、若化简|1－x|－，则x的取值范围是（）‎ ‎ A．X为任意实数 B．1≤X≤4‎ ‎ C．x≥1 D．x＜4 ‎ ‎18‎ c ‎32‎ ‎12‎ ‎15‎ a ‎20‎ ‎24‎ ‎25‎ b 表二 表三 表四 ‎3、阅读下面的文字后，回答问题：小明和小芳解答题目：“先化简下式，再求值：a+其中a=9时”，得出了不同的答案 ，小明的解答：原式= a+= a+(1－a)=1，小芳的解答：原式= a+(a－1)=2a－1=2×9－1=17‎ ‎⑴___________是错误的；‎ ‎ ⑵错误的解答错在未能正确运用二次根式的性质：‎ ‎ ________‎ ‎4、计算：‎ ‎5、我国1990年的人口出生数为23784659人。保留三个有效数字的近似值是　　　　人。‎ 六、综合应用 1、 已知△ABC的三边长分别为a、b、c, 且a、b、c满足a2 －6a+9+，试判断△ABC的形状．‎ ‎2、数轴上的点并不都表示有理数，如图l－2－2中数轴上的点P所表示的数是”，这种说明问题的方式体现的数学思想方法叫做（ ）‎ ‎ A．代人法B．换无法C．数形结合D．分类讨论 ‎3、（开放题）如图l－2－3所示的网格纸，每个小格均为正方形，且小正方形的边长为1，请在小网格纸上画出一个腰长为无理数的等腰三角形．‎ ‎4、如图1－2－4所示，在△ABC中，∠B=90○ ,点P从点B开始沿BA边向点A以 1厘米／秒的宽度移动；同时，点Q也从点B开始沿 BC边向点C以 2厘米/秒的速度移动，问几秒后，△PBQ的面积为36平方厘米？‎ ‎5、观察表一，寻找规律．表二、表三、表四分别是从表一中截取的一部分，其中a、b、c的值分别为 ‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎…‎ ‎3‎ ‎6‎ ‎9‎ ‎12‎ ‎…‎ ‎4‎ ‎8‎ ‎12‎ ‎16‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ A．20、29、30 B．18、30、26 ‎ C．18、20、26 D．18、30、28‎ 专题二 整式 一、考点扫描 ‎1、代数式的有关概念．‎ ‎(1)代数式是由运算符号把数或表示数的字母连结而成的式子．‎ ‎(2)求代数式的值的方法：①化简求值，②整体代人 ‎2、整式的有关概念 ‎(1)单项式：只含有数与字母的积的代数式叫做单项式．‎ ‎(2)多项式：几个单项式的和，叫做多项式 ‎(3)多项式的降幂排列与升幂排列 ‎(4)同类项：所含字母相同，并且相同字母的指数也分别相同的项，叫做同类顷．‎ ‎3、整式的运算 ‎(1)整式的加减：几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接．整式加减的一般步骤是：‎ ‎(2)如果遇到括号．按去括号法则先去括号：括号前是“十”号，把括号和它前面的“+”号去掉。括号里各项都不变符号，括号前是“一”号，把括号和它前面的“一”号去掉．括号里各项都改变符号．‎ ‎(3)合并同类项： 同类项的系数相加，所得的结果作为系数．字母和字母的指数不变．‎ ‎4、乘法公式 ‎(1).平方差公式:‎ ‎(2).完全平方公式: ‎ ‎5、因式分解 ‎(1).多项式的因式分解，就是把一个多项式化为几个整式的积．分解因式要进行到每一个因式都不能再分解为止．‎ ‎(2).分解因式的常用方法有：提公因式法和运用公式法 二、考点训练 ‎1、－的系数是 ，是 次单项式；‎ ‎2、多项式3x2－1－6x5－4x3是 次 项式，其中最高次项是 ，常数项是 ，三次项系数是 ，按x的降幂排列 ；‎ ‎3、如果3m7xny+7和-4m2-4yn2x是同类项，则x= ,y= ；这两个单项式的积是＿＿。‎ ‎4、下列运算结果正确的是（ ）‎ ‎①2x3-x2=x ②x3•(x5)2=x13 ③(-x)6÷(-x)3=x3 ④(0.1)-2•10-1=10‎ ‎（A）①② （B）②④ （C）②③ （D）②③④‎ ‎5、若x2＋2（m－3）x＋16 是一个完全平方式，则m的值是（　　）‎ ‎6、代数式a2－1，0,,x+，－，m，,–3b中单项式是 ，多项式是 ，分式是 。‎ 三、例题剖析 ‎1、设ａ－ｂ＝－2，求－ａｂ的值。‎ ‎2、若的积中不含有和项，求p、q的植。‎ ‎3、从边长为a的正方形内去掉一个边长为b的小正方形（如图1），然后将剩余部分剪拼成一个矩形（如图2），上述操作所能验证的等式是（ ）‎ ‎ A．a2-b2=（a+b）（a-b） B.（a-b）2=a2-2ab+b2‎ C.（a+b）2=a2+2ab+b2 D．a2+ab=a（a+b）‎ 四、综合应用 ‎1、将连续的自然数1至36按右图的方式排成一个正方形阵列，用一个小正方形任意圈出其中的9个数，设圈出的9个数的中心的数为a，用含有a的代数式表示这9个数的和为__________．‎ ‎2、用火柴棒按下图中的方式搭图形．‎ ‎（1）按图示规律填空：‎ 第n个图形 ‎1‎ ‎2‎ ‎3‎ ‎……‎ 火柴棒根数 ‎（2）按照这种方式搭下去，搭第n个图形需要_________根火柴棒．‎ ‎3、右边是一个有规律排列的数表，请用含n的代数式（n为正整数），表示数表中第n行第n列的数：______________．‎ 专题三 分式 一、考点扫描 ‎1．分式：整式A除以整式B，可以表示成的形式，如果除式B中含有字母，那么称为分式．‎ 注：（1）若B≠0，则有意义；（2）若B=0，则无意义；（2）若A=0且B≠0，则=0 ‎ ‎2．分式的基本性质：分式的分子与分母都乘以（或除以）同一个不等于零的整式，分式的值不变．‎ ‎3．约分：把一个分式的分子和分母的公团式约去，这种变形称为分式的约分．‎ ‎4．通分：根据分式的基本性质，异分母的分式可以化为同分母的分式，这一过程称为分式的通分．‎ ‎5．分式的加减法法则：‎ ‎（1）同分母的分式相加减，分母不变，把分子相加 ‎（2）异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法则进行计算．‎ ‎6．分式的乘除法法则：两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母；两个分式相除，把除式的分子和分母颠倒位置后 再与被除式相乘．‎ ‎7．通分注意事项：‎ ‎（1）通分的关键是确定最简公分母，最简公分母应为各分母系救的最小公倍数与所有相同因式的最高次幂的积；‎ ‎（2）易把通分与去分母混淆，本是通分，却成了去分母，把分式中的分母丢掉．‎ ‎8．分式的混合运算顺序，先算乘方，再算乘除，最后算加减，有括号先算括号里面的．‎ ‎9．对于化简求值的题型要注意解题格式，要先化简，再代人字母的值求值．‎ 二、考点训练 ‎1、已知分式当x≠______时，分式有意 ‎ 义；当x=______时，分式的值为0． ‎ ‎2、若将分式(a、b均为正数）中的字母a、b的值 ‎ 分别扩大为原来的2倍，则分式的值为（ ）‎ ‎ A．扩大为原来的2倍 B．缩小为原来的 ‎ ‎ C．不变 D．缩小为原来的 ‎3、分式，当x 时分式值为正；当整数 x= 时分式值为整数。‎ ‎4、计算所得正确结果为（ ）‎ ‎ ‎ ‎5、若，则= 。‎ ‎6、若=___‎ 三、例题剖析 ‎1、求值：‎ ‎2、（2005、河南，8分）有一道题“先化简，再求值：，其中。”小玲做题时把“”错抄成了“”，但她的计算结果也是正确的，请你解释这是怎么回事？‎ ‎3、已知：P=，Q=(x+y)2 －2y(x-y)，小敏、小聪每人在x－2，y—2的条件下分别计算了P和Q的值，小敏说P的值比Q大，小聪说C的值比P大．请你判断谁的结论正确，并说明理由．‎ ‎3、已知：‎ ‎4、若无论x为何实数，分式总有意义，则m的取值范围是 。 ‎ 四、综合应用 ‎1、已知△ABC的三边为a，b，c，=‎ ‎，试判定三角形的形状．‎ ‎2、(阅读理解题）阅读下面的解题过程，然后解题：‎ ‎ 题目：已知 求x+y+z+的值 ‎ 解：设=k, ，‎ ‎ ，‎ ‎ 仿照上述方法解答下列问题：‎ ‎ 已知：‎ ‎ ‎ 专题四 二次根式 一、考点扫描 ‎1．二次根式的有关概念 ‎(1)二次根式 ‎ 叫做二次根式．注意被开方数只能是正数或O．‎ ‎(2)最简二次根式 ‎ 被开方数所含因数是整数，因式是整式，不含能开得尽方的因数或因式的二次根式，叫做最简二次根式．‎ ‎(3)同类二次根式 ‎ 化成最简二次根式后，被开方数相同的二次根式，叫做同类二次根式．‎ ‎2．二次根式的性质 ‎3．二次根式的运算 ‎(1)二次根式的加减 ‎①先把各个二次根式化成最简二次根式；‎ ‎②再把同类三次根式分别合并 ‎(2)三次根式的乘法 ‎(3)二次根式的除法 二、考点训练 ‎1、（2006年南通市）式子有意义的x取值范围是________．‎ ‎2、（2006年海淀区）下列根式中能与合并的二次根式为（ ）‎ ‎ A、 B、 C、 D、‎ ‎3、（06烟台市）若 ，则 =______．‎ ‎4、（2005年福州市）下列各式中属于最简二次根式的是（ ）‎ A、 B、C、 D、‎ ‎5、（2006年连云港市）能使等式成立的x的取值范围是（ ）‎ A．x≠2 B．x≥0 C．x>2 D．x≥2‎ ‎6、（2005年长沙市）小明的作业本上有以下四题：‎ ‎①=4a；②a；‎ ‎③a；④（a≠0），做错的题是（ ）‎ A．① B．② C．③ D．④‎ ‎7、对于实数a、b，若=b-a，则（ ）‎ A．a>b B．a0，b>0）分别作如下的变形：‎ 甲 =; ‎ 乙：=.‎ ‎ 这两种变形过程的下列说法中，正确的是（ ） A．甲、乙都正确 B．甲、乙都不正确 ‎ C．只有甲正确 D．只有乙正确 ‎5、‎ 四、综合应用 ‎1、（2006年内江市）对于题目“化简求值： ，其中a=”甲、乙两人的解答不同．‎ 甲的解答是： =‎ ‎=‎ 乙的解答是：=‎ ‎=，‎ 谁的解答是错误的是，为什么？‎ ‎2、（2006年桂林市）观察下列分母有理化的计算:‎ ‎ …‎ 从计算结果中找出规律利用规律计算:‎ ‎3、如果ａ＋ｂ＋｜－1｜＝4＋2－4，那么ａ＋2ｂ－3ｃ的值