- 2021-06-26 发布 |
- 37.5 KB |
- 6页

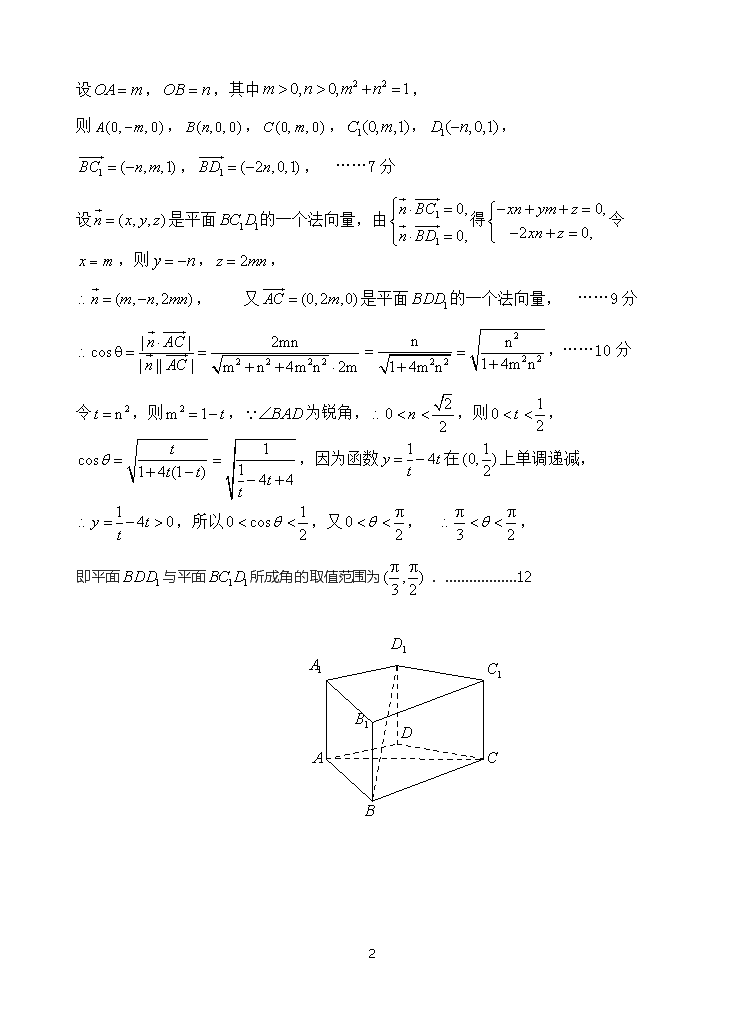

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018年达利教育卓越奖初中学科竞赛高二数学参考答案
2018年高中学科竞赛 高二数学试题 (试卷总分100分,考试时间120分钟) 一、选择题(每小题5分,共30分) 题号 1 2 3 4 5 6 答案 B D C B D A 二、填空题(每小题5分,共30分) 7.4; 8.; 9. ; 10.; 11.; 12.. 三、解答题(本大题共3小题,共40分) 13.(本小题满分12分) 【解析】 (Ⅰ)条件②,可做为的充分条件. ……1分 证明如下: 平面,,平面, ……2分 ∵平面,. 若条件②成立,即, ∵,平面, ……3分又平面,. …..4分 (Ⅱ)由已知,得是菱形,.设,为的中点, 则平面,∴、、交于同一点且两两垂直. …5分 以分别为轴建立空间直角坐标系,如图所示. 5 设,,其中, 则,,,,, ,, ……7分 设是平面的一个法向量,由得令,则,, , 又是平面的一个法向量, ……9分 ,……10分 令,则,为锐角,,则,,因为函数在上单调递减,,所以,又, , 即平面与平面所成角的取值范围为. ………………12 5 14.(本小题满分14分) 解法1:(1)①若直线∥轴,则点为.----1分 ②设直线,并设点的坐标分别是, 由消去,得 , (*) 由直线与椭圆有两个不同的交点,可得, 所以.由及方程(*),得, , 即消去,并整理得,(.综上所述,点的轨迹方程为(.---7分 (2)①当∥轴时,分别是椭圆长轴的两个端点,则点在原点处, 所以,,所以,. ----9分 ②由方程(*),得所以,, , 所以. 因为,所以,所以. 综上所述,.--14分 5 解法2:(1)①若直线∥轴,则点为. --1分 ②设直线, 并设点的坐标分别是, 由消去,得 , (*) 由直线与椭圆有两个不同的交点,可得,即,所以. 由及方程(*),得, ,即 由于(否则,直线与椭圆无公共点),消去,并整理得,(.综上所述,点的轨迹方程为(.--7分 (2)①当∥轴时,分别是椭圆长轴的两个端点,则点在原点处, 所以,,所以,. --9分 ②由方程(*),得 所以,, , 所以.因为,所以,所以.综上所述,.--14分 5 15.(本小题满分14分) 【解析】(1)设直线与相切于点,依题意得,解得,所以,经检验:符合题意.-------3分 (2)由(1)得,所以,当, 时, ,所以在上单调递减,所以当, 时, , ,当时, ,所以在上单调递增,所以当时, ,依题意得,所以,解得.-----8分 (3) 依题意得,两式相减得,所以,方程可转化为,即,令,则,则 5 ,令,因为,所以在上单增,所以,所以,即-----14分 5查看更多