高三数学二轮高考专题辅导与训练打包检测试题：专题七第1讲课时训练提能

高三数学二轮高考专题辅导与训练打包检测试题：专题七第1讲课时训练提能

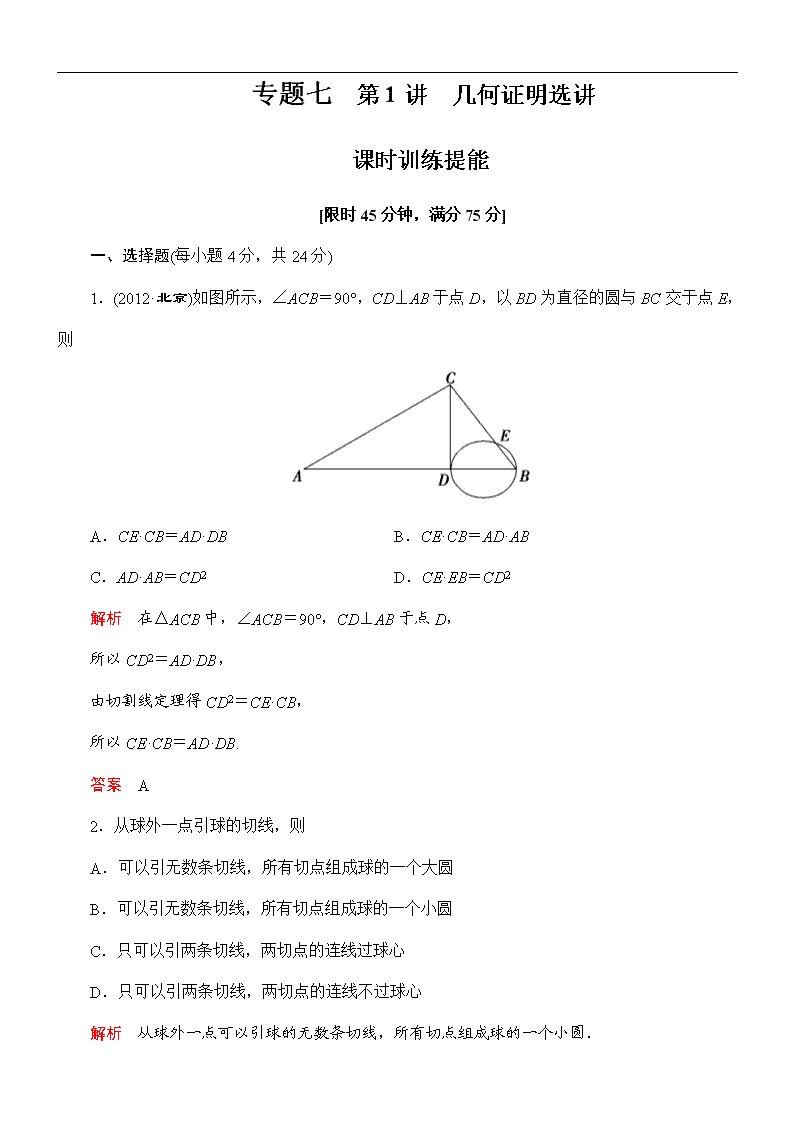
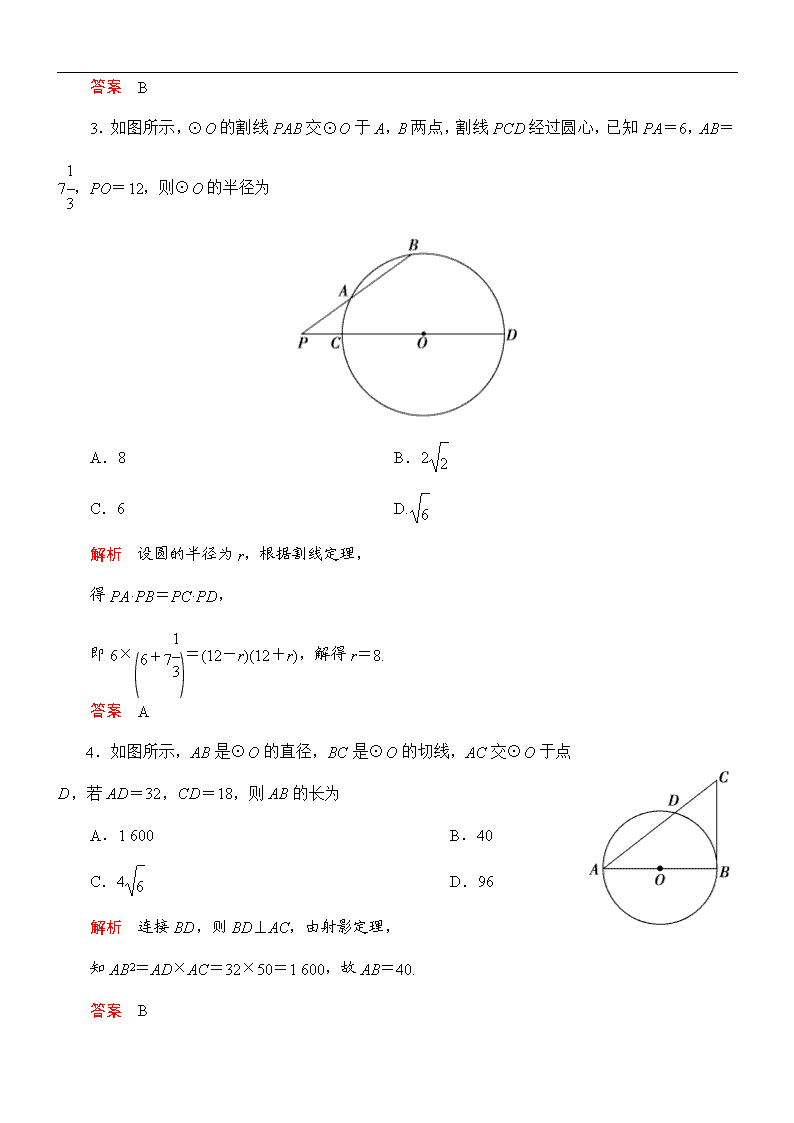
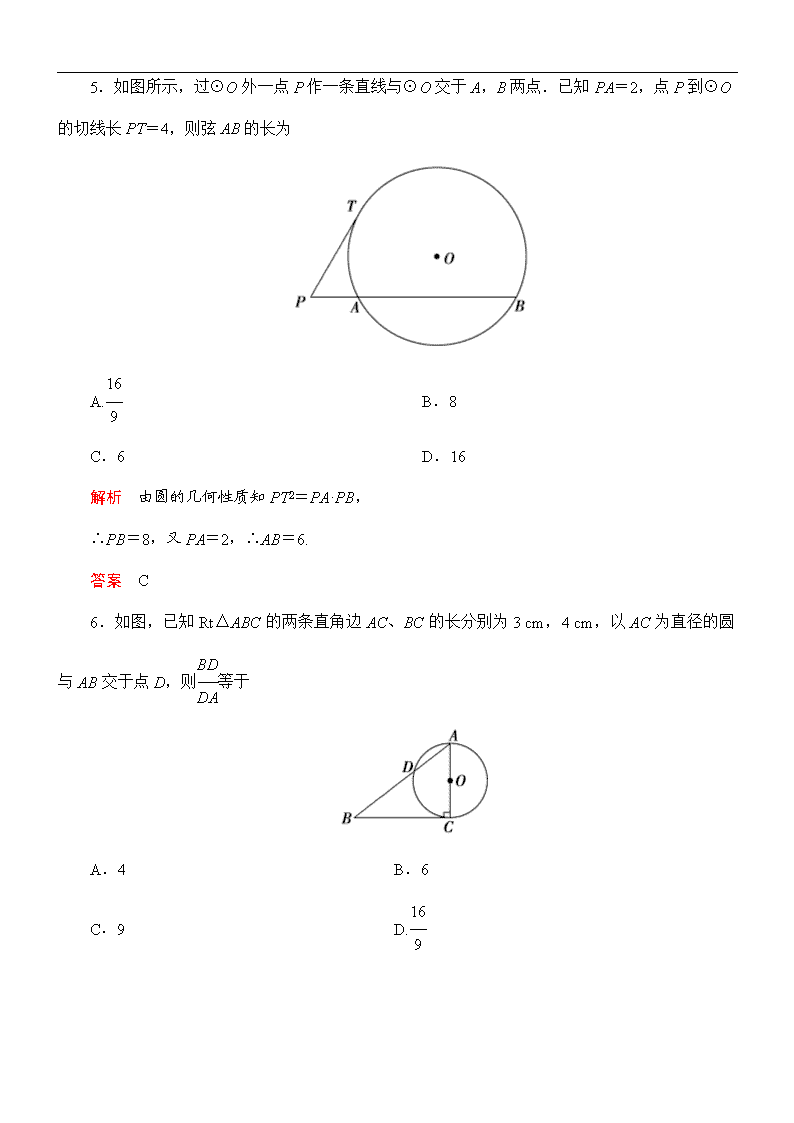
专题七 第1讲　几何证明选讲 课时训练提能 ‎[限时45分钟，满分75分]‎ 一、选择题(每小题4分，共24分)‎ ‎1．(2012·北京)如图所示，∠ACB＝90°，CD⊥AB于点D，以BD为直径的圆与BC交于点E，则 A．CE·CB＝AD·DB　　　 B．CE·CB＝AD·AB C．AD·AB＝CD2 D．CE·EB＝CD2‎ 解析　在△ACB中，∠ACB＝90°，CD⊥AB于点D，‎ 所以CD2＝AD·DB，‎ 由切割线定理得CD2＝CE·CB，‎ 所以CE·CB＝AD·DB.‎ 答案　A ‎2．从球外一点引球的切线，则 A．可以引无数条切线，所有切点组成球的一个大圆 B．可以引无数条切线，所有切点组成球的一个小圆 C．只可以引两条切线，两切点的连线过球心 D．只可以引两条切线，两切点的连线不过球心 解析　从球外一点可以引球的无数条切线，所有切点组成球的一个小圆．‎ 答案　B ‎3．如图所示，⊙O的割线PAB交⊙O于A，B两点，割线PCD经过圆心，已知PA＝6，AB＝7，PO＝12，则⊙O的半径为 A．8　　　　 B．‎2‎ C．6　　　　 D. 解析　设圆的半径为r，根据割线定理，‎ 得PA·PB＝PC·PD，‎ 即6×＝(12－r)(12＋r)，解得r＝8.‎ 答案　A ‎4．如图所示，AB是⊙O的直径，BC是⊙O的切线，AC交⊙O于点D，若AD＝32，CD＝18，则AB的长为 A．1 600 　　　 B．40‎ C．4 　　　 D．96‎ 解析　连接BD，则BD⊥AC，由射影定理，‎ 知AB2＝AD×AC＝32×50＝1 600，故AB＝40.‎ 答案　B ‎5．如图所示，过⊙O外一点P作一条直线与⊙O交于A，B两点．已知PA＝2，点P到⊙O 的切线长PT＝4，则弦AB的长为 A. B．8‎ C．6 D．16‎ 解析　由圆的几何性质知PT2＝PA·PB，‎ ‎∴PB＝8，又PA＝2，∴AB＝6.‎ 答案　C ‎6．如图，已知Rt△ABC的两条直角边AC、BC的长分别为‎3 cm，‎4 cm，以AC为直径的圆与AB交于点D，则等于 A．4 B．6‎ C．9 D. 解析　连接CD.‎ ‎∵AC为⊙O的直径，∴CD⊥AD.‎ ‎∵△ABC为直角三角形．‎ ‎∴AC2＝AD·AB，BC2＝BD·AB，∴＝＝＝.‎ 答案　D 二、填空题(每小题5分，共15分)‎ ‎7．(2012·东莞高级中学二模)如图所示，AB是半径等于3的⊙O的直径，CD是⊙O的弦，BA，DC的延长线交于点P，若PA＝4，PC＝5，则∠CBD＝________.‎ 解析　连接AC，DO，OC，由圆内接四边形的对角互补可得△PAC∽△PDB，‎ ‎∴＝.‎ ‎∴PD＝8，CD＝3.‎ 又OC＝OD＝3，∴△OCD为等边三角形．‎ ‎∴∠COD＝60°，∴∠CBD＝∠COD＝30°.‎ 答案　30°‎ ‎8．(2012·汕头高三模拟)如图所示，圆的内接三角形ABC的角平分线BD与AC交于点D，与圆交于点E，连接AE，已知ED＝3，BD＝6，则线段AE＝________.‎ 解析　∵∠CBE＝∠CAE，BD为角平分线，‎ ‎∠AED＝∠AEB，∴△ADE∽△BAE.‎ ‎∴＝.∴AE2＝DE·BE＝3×9.∴AE＝3.‎ 答案　3 ‎9．(2012·广东)如图所示，圆O的半径为1，A，B，C是圆周上的三点，满足∠ABC＝30°，过点A作圆O的切线与OC的延长线交于点P，则PA＝________.‎ 解析　解法一　连接OA得∠AOP＝60°，所以OP＝2，PC＝1，‎ 所以PA2＝PC×(PC＋2)＝1×3，所以PA＝.‎ 解法二　延长PO交圆于点D，连接AD、OA，‎ 则∠D＝∠B＝30°，因为OA＝OD，‎ 所以∠DAO＝∠D＝30°，‎ 又因为OA⊥PA，所以∠P＝180°－90°－30°－30°＝30°，‎ 所以PA＝AD，在△AOD中，由余弦定理得，‎ AD＝＝，‎ 故PA＝.‎ 答案　 三、解答题(每小题12分，共36分)‎ ‎10．(2012·南通第一次调研)锐角三角形ABC内接于⊙O，∠ABC＝60°，∠BAC＝40°，作OE⊥AB交劣弧于点E，连接EC，求∠OEC.‎ 解析　连接OC.∵∠ABC＝60°，∠BAC＝40°，‎ ‎∴∠ACB＝80°.‎ ‎∵OE⊥AB，∴E为的中点，‎ ‎∴和所对的圆心角均为80°.‎ ‎∴∠EOC＝80°＋80°＝160°，∴∠OEC＝10°.‎ ‎11．(2012·大荔城郊中学二模)如图，△ABC内接于圆O，AB＝AC，直线MN切圆O于点C，BD∥MN，AC与BD相交于点E.‎ ‎(1)求证：AE＝AD；‎ ‎(2)若AB＝6，BC＝4，求AE.‎ 解析　(1)证明　∵BD∥MN，∴∠AED＝∠ACN.‎ 又MN为圆的切线，∴∠ACN＝∠ABC.‎ 则∠AED＝∠ABC.‎ ‎∵AB＝AC，∴∠ABC＝∠ACB.‎ ‎∴∠ACB＝∠AED。‎ ‎∵∠ADB＝∠ACB，∴∠AED＝∠ADB，‎ ‎∴AE＝AD.‎ ‎(2)∵∠ACD＝∠ABD，∠CAD＝∠CAB且AE＝AD，‎ ‎∴△ABE≌△ACD.‎ ‎∴BE＝CD＝BC＝4.‎ 设AE＝x，易证△ABE∽△DCE，DE＝x，‎ 又AE·EC＝BE·ED，∴x＝.‎ ‎12．(2012·辽宁)如图，⊙O和⊙O′相交于A，B两点，过A作两圆的切线分别交两圆于C，D两点，连接DB并延长交⊙O于点E.证明：‎ ‎(1)AC·BD＝AD·AB；‎ ‎(2)AC＝AE.‎ 证明　(1)由AC与⊙O′相切于A，得∠CAB＝∠ADB，同理∠ACB＝∠DAB，所以△ACB∽△DAB.‎ 从而＝，‎ 即AC·BD＝AD·AB.‎ ‎(2)由AD与⊙O相切于A，得∠AED＝∠BAD.‎ 又∠ADE＝∠BDA，得△EAD∽△ABD.‎ 从而＝，即AE·BD＝AD·AB.‎ 结合(1)的结论知，AC＝AE.‎