- 2021-06-24 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高中数学 第三章简单的线性规划问题
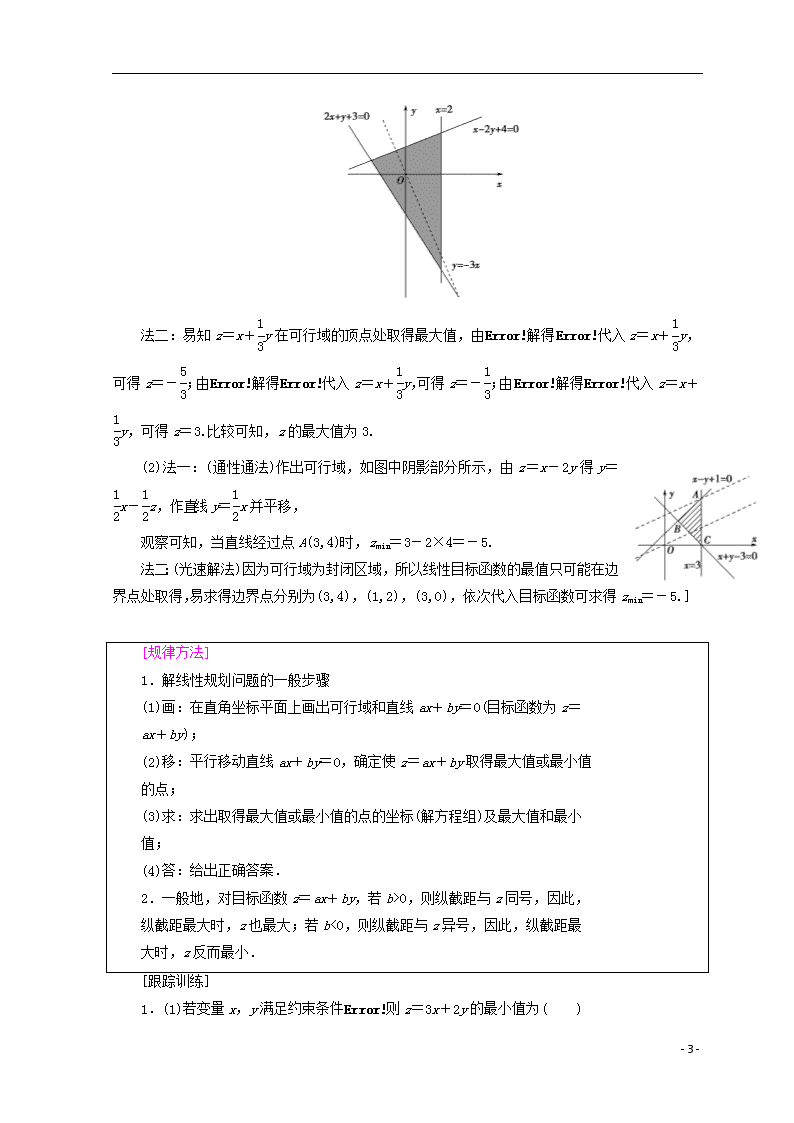
第1课时 简单的线性规划问题 学习目标:1.了解线性规划的意义,以及约束条件、目标函数、可行解、可行域,最优解等基本概念(重点).2.理解目标函数的最大、小值与其对应直线的截距的关系(易混点). [自 主 预 习·探 新 知] 1.线性规划中的基本概念 名称 意义 约束条件 由变量x,y组成的不等式组 线性约束条件 由x,y的一次不等式(或方程)组成的不等式组 目标函数 欲求最大值或最小值所涉及的变量x,y的函数解析式 线性目标函数 关于x,y的一次解析式 可行解 满足线性约束条件的解(x,y) 可行域 所有可行解组成的集合 最优解 使目标函数取得最大或最小值的可行解 线性规划问题 在线性约束条件下求线性目标函数的最大值或最小值问题 思考:在线性约束条件下,最优解唯一吗? [提示] 不一定,可能只有一个,可能有多个,也可能有无数个. 2.线性目标函数的最值 线性目标函数z=ax+by(b≠0)对应的斜截式直线方程是y=-x+,它表示斜率为-,在y轴上的截距是的一条直线,当z变化时,方程表示一组互相平行的直线. 当b>0,截距最大时,z取得最大值,截距最小时,z取得最小值; 当b<0,截距最大时,z取得最小值,截距最小时,z取得最大值. 思考:若将目标函数z=x+y看成直线方程时,z具有怎样的几何意义? [提示] 把目标函数整理可得y=-x+z,z为直线在y轴上的截距. [基础自测] 1.思考辨析 (1)可行域是一个封闭的区域.( ) (2)在线性约束条件下,最优解是唯一的.( ) (3)最优解一定是可行解,但可行解不一定是最优解.( ) (4)线性规划问题一定存在最优解.( ) [答案] (1)× (2)× (3)√ (4)× 提示: - 9 - (1)错误.可行域是约束条件表示的平面区域,不一定是封闭的.(2)错误.在线性约束条件下,最优解可能有一个或多个,也可能有无数个,也可能无最优解,故该说法错误.(3)正确.满足线性约束条件的解称为可行解,但不一定是最优解,只有使目标函数取得最大值或最小值的可行解,才是最优解,所以最优解一定是可行解.(4)错误.线性规划问题不一定存在可行解,存在可行解也不一定存在最优解,故该说法是错误的. 2.若则z=x-y的最大值为________. 1 根据题意作出不等式组所表示的可行域如图阴影部分所示.令z=0,作直线l:y-x=0.当直线l向下平移时,所对应的z=x-y的函数值随之增大,当直线l经过可行域的顶点M时,z=x-y取得最大值.顶点M是直线x+y=1与直线y=0的交点,解方程组得顶点M的坐标为(1,0),代入z=x-y,得zmax=1.] 3.已知x,y满足且z=2x+4y的最小值为-6,则常数k=________. 【导学号:91432320】 0 [当直线z=2x+4y经过两直线x=3与x+y+k=0的交点(3,-3-k)时,z最小,所以-6=2×3+4(-3-k),解得k=0.] 4.已知点P(x,y)的坐标满足条件点O为坐标 原点,那么PO的最小值等于________,最大值等于________. [如图所示,线性区域为图中阴影部分,PO指线性区域内的点到原点的距离,所以最短为=,最长为=.] [合 作 探 究·攻 重 难] 求线性目标函数的最值问题 (1)(2018·全国卷Ⅲ)若变量x,y满足约束条件则z=x+y的最大值是________. (2)若x,y满足约束条件则z=x-2y的最小值为________. (1)3 (2)-5 [(1)法一:作出不等式组表示的平面区域如图中阴影部分所示,画出直线y=-3x,平移该直线,由图可知当平移后的直线经过直线x=2与直线x-2y+4=0的交点(2,3)时,z=x+y取得最大值,即zmax=2+×3=3. - 9 - 法二:易知z=x+y在可行域的顶点处取得最大值,由解得代入z=x+y,可得z=-;由解得代入z=x+y,可得z=-;由解得代入z=x+y,可得z=3.比较可知,z的最大值为3. (2)法一:(通性通法)作出可行域,如图中阴影部分所示,由z=x-2y得y=x-z,作直线y=x并平移, 观察可知,当直线经过点A(3,4)时,zmin=3-2×4=-5. 法二:(光速解法)因为可行域为封闭区域,所以线性目标函数的最值只可能在边界点处取得,易求得边界点分别为(3,4),(1,2),(3,0),依次代入目标函数可求得zmin=-5.] [规律方法] 1.解线性规划问题的一般步骤 (1)画:在直角坐标平面上画出可行域和直线ax+by=0(目标函数为z= ax+by); (2)移:平行移动直线ax+by=0,确定使z=ax+by取得最大值或最小值 的点; (3)求:求出取得最大值或最小值的点的坐标(解方程组)及最大值和最小 值; (4)答:给出正确答案. 2.一般地,对目标函数z=ax+by,若b>0,则纵截距与z同号,因此, 纵截距最大时,z也最大;若b<0,则纵截距与z异号,因此,纵截距最 大时,z反而最小. [跟踪训练] - 9 - 1.(1)若变量x,y满足约束条件则z=3x+2y的最小值为( ) A.4 B. C.6 D. (2)变量x,y满足约束条件若z=2x-y的最大值为2,则实数m等于( ) A.-2 B.-1 C.1 D.2 (1)B (2)C [(1)不等式组表示的平面区域为如图所示的阴影部分,作直线l0:3x+2y=0,平移直线l0,当经过点A时,z取得最小值. 此时∴A,∴zmin=3×1+2×=. (2)对于选项A,当m=-2时,可行域如图(1),直线y=2x-z的截距可以无限小,z不存在最大值,不符合题意,故A不正确; 对于选项B,当m=-1时,mx-y≤0等同于x+y≥0,可行域如图(2),直线y=2x-z的截距可以无限小,z不存在最大值,不符合题意,故B不正确; 对于选项C,当m=1时可行域如图(3),当直线y=2x-z过点A(2,2)时截距最小,z最大为2,满足题意,故C正确; 对于选项D,当m=2时,可行域如图(4),直线y=2x-z与直线2x-y=0平行,截距最小值为0,z最大为0,不符合题意,故D不正确.故选C. - 9 - ] 非线性目标函数的最优解问题 [探究问题] 1.目标函数z=x2+y2和z=(x-a)2+(y-b)2的几何意义是什么? 提示:z=x2+y2表示可行域内的点(x,y)到坐标原点的距离的平方;z=(x-a)2+(y-b)2表示可行域内的点(x,y)到定点(a,b)的距离的平方. 2.目标函数z=(x≠a)和z=(ac≠0)表示的几何意义是什么? 提示:z=(x≠a)表示可行域内的点(x,y)与定点(a,b)的连线的斜率;z==·,表示可行域内的点(x,y)与定点的连线的斜率的倍. 3.z=|ax+by+c|(a2+b2≠0)的几何意义是什么? 提示:z=|ax+by+c|=·,表示可行域内的点(x,y)到直线ax+by+c=0的距离的倍. 已知,求: (1)z=x2+y2-10y+25的最小值; (2)z=的范围. 【导学号:91432323】 思路探究:①把z=x2+y2-10y+25化为z=x2+(y-5)2,其几何意义是什么?②把z= - 9 - 化为z=2·,其几何意义是什么? [解] 作出可行域如图,并求出顶点的坐标A(1,3),B(3,1),C(7,9). (1)z=x2+y2-10y+25=x2+(y-5)2表示可行域内任一点(x,y)到定点M(0,5)的距离的平方,过M作直线AC的垂线,易知垂足N在线段AC上,故z的最小值是|MN|2=. (2)z==2·表示可行域内任一点(x,y)与定点Q连线的斜率的2倍,因为kQA=,kQB=,故z的范围为. 母题探究:1.本例中的条件不变求z=|x+2y-4|的最大值. [解] 作出不等式组表示的平面区域,如图中阴影部分所示. 法一:z=|x+2y-4|=×,其几何意义为阴影区域内的点到直线x+2y-4=0的距离的倍.由得点B的坐标为(7,9),显然点B到直线x+2y-4=0的距离最大,此时zmax=21. 法二:由图可知,阴影区域(可行域)内的点都在直线x+2y-4=0的上方,显然此时有x+2y-4>0,于是目标函数等价于z=x+2y-4,即转化为一般的线性规划问题.显然当直线经过点B时,目标函数z取得最大值,由得点B的坐标为(7,9),此时zmax=21. 2.本例题中的条件不变 (1)求z=x2+y2的最小值. (2)求z=的范围. - 9 - [解] (1)由z=x2+y2的几何意义为区域内的点(x,y)至(0,0)的距离的平方知,z的最小值为(0,0)到直线x+y-4=0的距离的平方. ∴zmin=2=8. (2)由z=的几何意义为区域内的点(x,y)与原点连线的斜率.因为A(1,3),B(3,1),kOA=3.kOB=, ∴z的取值范围是. [规律方法] 1.利用线性规划求最值,关键是理解线性目标函数的几何意义,从本 题的求解过程可以看出,最优解一般在可行域的边界上,并且通常在可 行域的顶点处取得,所以作图时要力求准确. 2.非线性目标函数的最值的求解策略 (1)z=(x-a)2+(y-b)2型的目标函数可转化为点(x,y)与点(a,b)距离的 平方,特别地,z=x2+y2型的目标函数表示可行域内的点到原点的距离 的平方. (2)z=型的目标函数可转化为点(x,y)与点(a,b)连线的斜率. (3)z=|Ax+By+C|可转化为点(x,y)到直线Ax+By+C=0的距离的 倍. 已知目标函数的最值求参数 已知约束条件且目标函数z=a2x+(a-2-a2)y取得最小值的最优解唯一,为(2,2),则a的取值范围是________. 思路探究:本题中的目标函数中两个元的系数都含有参数,因此需要研究参数的几何意义和符号特征,注意到a-2-a2的判别式非正,且a2≥0,又最小值的最优解唯一,从而斜率范围可以确定. [线性约束条件所表示的区域如图中阴影部分所示. 由于目标函数的y的系数a-2-a2=-2-<0,x的系数a2≥0,故平行直线系z=a2x+(a-2-a2)y的斜率非负,为 - 9 - .由于是最小值问题且最优解唯一,为图中的点A(2,2),从而只需<,解得查看更多