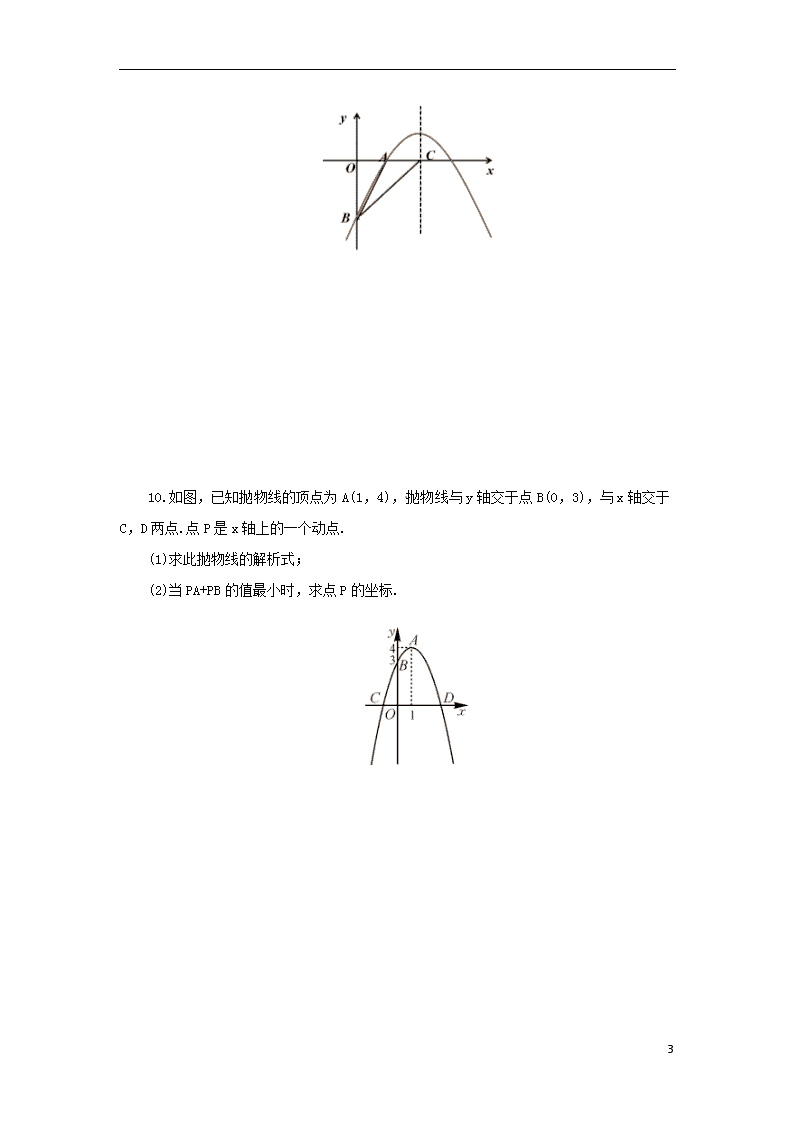2020九年级数学上册 第二十二章 用待定系数法求二次函数的解析式
22.1.4 用待定系数法求二次函数的解析式
第2课时
1.抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
-1
0
1
2
3
4
…
y
…
1
3
1
…
从上表可知,下列说法错误的是( )
A.对称轴为直线x=2 B.开口向下
C.顶点坐标为(2,3) D.当x=5时,
2.若,,为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是( )
A.y1
0;②4a+c>2b;③(a+c)2>b2;④x(ax+b)≤a-B.其中正确的是_____________.(请把正确结论的序号都填在横线上)
9.如图,已知二次函数的图象经过A(2,0),B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,
连接BA,BC,求△ABC的面积.
10
10.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
10
11.已知抛物线y=ax2+bx+c经过原点O及点A(-4,0)和点B(-6,3).
(1)求抛物线的解析式以及顶点坐标;
(2)如图,将直线y=2x沿y轴向下平移后与(1)中所求抛物线只有一个交点C,平移后的直线与y轴交于点D,求直线CD的解析式.
12.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,A点在原点的左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的解析式.
(2)连接PO,PC,并把△POC沿CO翻折,得到四边形POP'C,那么是否存在点P,使四边形POP'C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)求四边形ABPC面积最大时点P的坐标及四边形ABPC的最大面积.
10
13.通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.
(1)当0≤x≤10时,求注意力指标数y与时间x的函数解析式;
(2)一道数学竞赛题需要讲解24分钟,问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
14.如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.
(1)求此抛物线的解析式.
(2)小明在探究点D运动时发现,①当点D与点C重合时,EF长度可看作0;②当点D与点O重合时,EF长度也可以看作0,于是他猜想:当点D运动到OC中点位置时,线段EF最长,你认为他的猜想是否正确,为什么?
(3)连接CF,DF,请直接写出△CDF为等腰三角形时所有t的值.
10
10
参考答案
1.D
2.B
3.D
4.D
5.y=x2-x-2
6.y=x2-x-2
7.600
8.①②④
9.(1)
(2)△ABC的面积是6.
10.解:(1)∵抛物线的顶点坐标为(1,4),∴设y=a(x-1)2+4.
∵抛物线过点B(0,3),∴3=a(0-1)2+4,解得a=-1.
∴抛物线的解析式为y=-(x-1)2+4,即y=-x2+2x+3.
(2)作点B关于x轴的对称点E(0,-3),连接AE交x轴于点P.
设AE解析式为y=kx+b,则k+b=4,
b=-3,解得k=7,b=-3.
∴yAE=7x-3.
∵当y=0时,x=,∴点P的坐标为(,0).
11.解:(1)∵抛物线经过(0,0),(-4,0),(-6,3)三点,
10
∴,解得
∴抛物线的解析式为 .
∵,
∴抛物线的顶点坐标为(-2,-1).
(2)设直线CD的解析式为y=2x+m,
根据题意,得,
化简整理,得x2-4x-4m=0,此方程只有一个解,
则∆=16+16m=0,解得m=-1,
∴直线CD的解析式为y=2x-1.
12.解:(1)将B,C两点的坐标代入y=x2+bx+c中,
得解得
∴二次函数的解析式为y=x2-3x-4.
(2)存在点P,使四边形POP'C为菱形.
如图(1),设P点坐标为(x,x2-3x-4),连接PP'交CO于点E,若四边形POP′C是菱形,则有PC=PO,且FE⊥CO,
∴OE=EC=2,
∴x2-3x-4=-2,解得(取负不合题意,舍去),
∴点P的坐标为.
10
(3)设点P的坐标为(x,x2-3x-4),如图(2).
S四边形ABPC=S△AOC+S△OPC+S△OPB
=-2x2+8x+10=-2(x2-4x)+10=-2(x-2)2+18,
∴当x=2时,四边形ABPC的面积最大,最大值为18.
此时点P的坐标为(2,-6).
13.解:(1)当0≤x≤10时,设抛物线的函数解析式为y=ax2+bx+c(a≠0),由于它的图象经过点(0,20),(5,39),(10,48),
所以,解得,,c=20,
所以,0≤x≤10.
(2)当20≤x≤40时,易求.
所以当0≤x≤10时,令y=36,得,
解得x=4,x=20(舍去);
当20≤x≤40时,令y=36,得,
解得.
因为,
所以老师可以经过适当的安排,在学生注意力指标数都不低于36时,讲解完这道竞赛题.
14.解:(1)设抛物线的解析式为y=ax2+bx+c,由题意得
,解得
∴抛物线的解析式为y=-x2+2x+3.
(2)他的猜想正确.理由如下:
设直线BC的解析式为y=mx+n,
10
把C(0,3),B(3,0)代入得 ,解得,则直线BC的解析式为y=-x+3.
设E(t,-t+3),则D(0,-t+3),F(t,-t2+2t+3),
∴
当时,EF最大,最大值为,此时D点坐标为,
∴点D为OC的中点时,线段EF最长.
(3)如图,连接DF,CF.
∵C(0,3),D(0,-t+3),F(t,-t2+2t+3),∴CD2=(-t+3-3)2=t2,
CF2=t2+(-t2+2t+3-3)2
=t2+(t2+2t)2,
DF2=t2+(-t2+2t+3+t-3)2=t2+(-t2+3t)2,
当CD=CF时,t2=t2+(-t2+2t)2,解得t1=0,t2=2;
当FC=FD时,t2+(-t2+2t)2=t2+(-t2+3t)2,解得t1=0,;
当DC=DF时,t2=t2+(-t2+3t)2,解得t1=0,t2=3.
综上所述,当t=2或或3时,△CDF为等腰三角形.
10