2017-2018学年四川省乐山沫若中学高二下学期期中考试数学（理）试题 Word版

2017-2018学年四川省乐山沫若中学高二下学期期中考试数学（理）试题 Word版

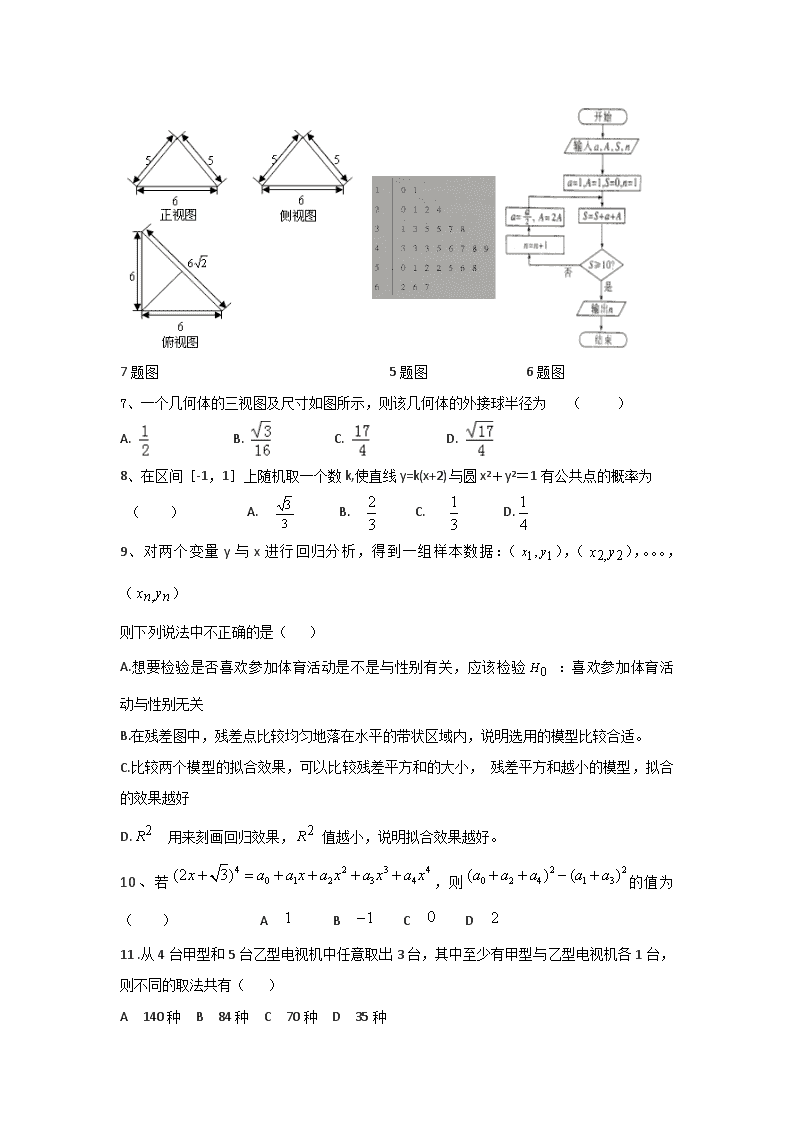
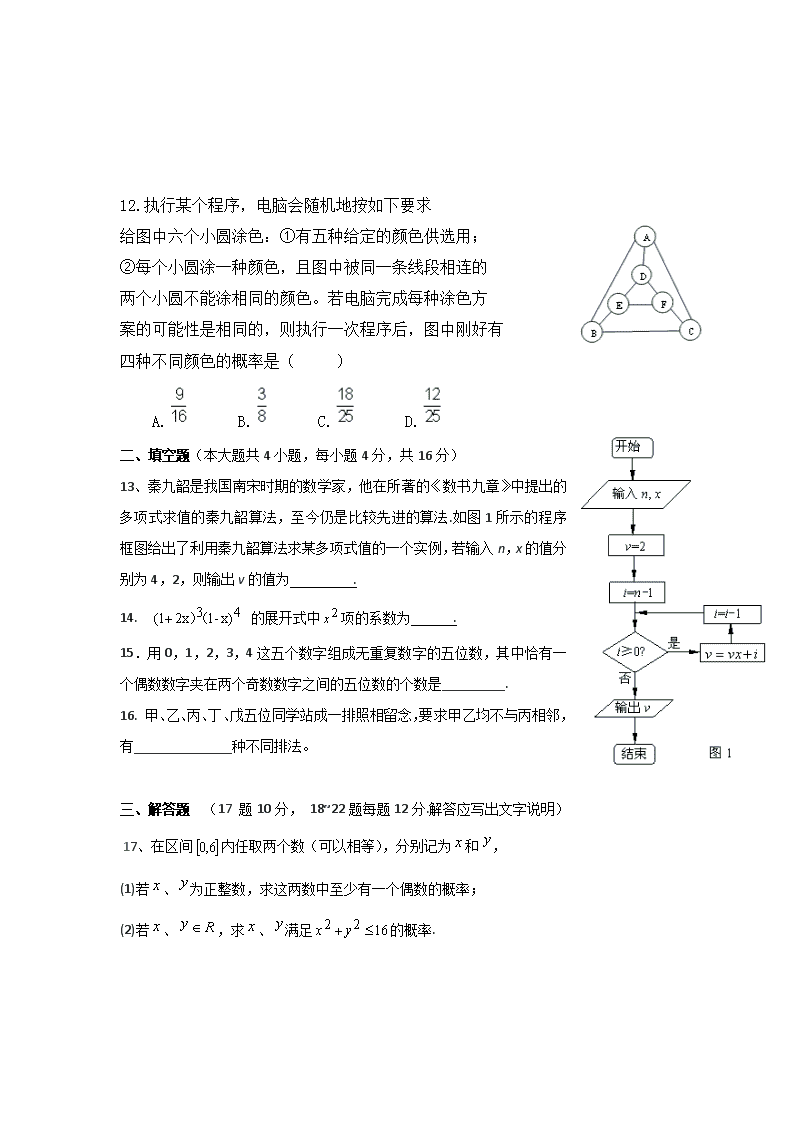
‎2017-2018学年四川省乐山沫若中学高二下学期期中考试数学(理)试卷 命题：鲁超群 一、选择题（本大题共12小题，每小题5分，共60分.）‎ ‎1、现有以下两项调查：①某校高二年级共有15个班，现从中选择2个班，检查其清洁卫生状况；②某市有大型、中型与小型的商店共1500家，三者数量之比为1∶5∶9．为了调查全市商店每日零售额情况，抽取其中15家进行调查．完成①、②这两项调查宜采用的抽样方法依次是（ ）‎ A. 简单随机抽样法，分层抽样法 B. 系统抽样法，简单随机抽样法 C．分层抽样法，系统抽样法 D．系统抽样法，分层抽样法 ‎ ‎2、下列等式不正确的是（ ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ ‎3、在投掷两枚硬币的随机试验中， 记“一枚正面朝上，一枚反面朝上” 为事件，“两枚正面朝上” 为事件，则事件，（ ）‎ A. 既是互斥事件又是对立事件 B. 是对立事件而非互斥事件 C．既非互斥事件也非对立事件 D．是互斥事件而非对立事件 ‎4．已知两组数据,的对应值如下表，若已知x,是线性相关的且线性回归方程为：经计算知：则 x ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ y ‎12‎ ‎10‎ ‎9‎ ‎8‎ ‎6‎ A. -0.6 B. ‎0.6 C. -17.4 D. 17.4‎ ‎5、我校政教处连续30天对同学们的着装进行检查，着装不合格的人数为如图所示的茎叶图，则中位数，众数，极差分别是（ ）‎ A 44，45，56 B 44，43，‎57 C 44,43，56 D 45，43,57‎ ‎6．我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现用程序框图描述，如图所示，则输出的结果为（ ）‎ A.5 B. ‎4 ‎C. 3 D.2 ‎ ‎7题图 5题图 6题图 ‎7、一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为 （　 　）‎ A. B. C. D. ‎ ‎8、在区间［-1，1］上随机取一个数k,使直线y=k(x+2)与圆x2＋y2＝1有公共点的概率为 ‎ （ ） A. B. C. D. ‎ ‎9、对两个变量y与x进行回归分析，得到一组样本数据：（），（），。。。，（）‎ 则下列说法中不正确的是（ ）‎ A.想要检验是否喜欢参加体育活动是不是与性别有关，应该检验 ：喜欢参加体育活 动与性别无关 B.在残差图中，残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适。‎ C.比较两个模型的拟合效果，可以比较残差平方和的大小， 残差平方和越小的模型，拟合的效果越好 ‎ D. 用来刻画回归效果， 值越小，说明拟合效果越好。‎ ‎10、若，则的值为（ ） A B C D ‎ ‎11 .从4台甲型和5台乙型电视机中任意取出3台，其中至少有甲型与乙型电视机各1台，则不同的取法共有（ ）‎ A 140种 B 84种 C 70种 D 35种 ‎ ‎12.执行某个程序，电脑会随机地按如下要求 给图中六个小圆涂色：①有五种给定的颜色供选用；‎ ‎②每个小圆涂一种颜色，且图中被同一条线段相连的 两个小圆不能涂相同的颜色。若电脑完成每种涂色方 案的可能性是相同的，则执行一次程序后，图中刚好有 四种不同颜色的概率是（ ）‎ A. B. C. D.‎ 二、填空题（本大题共4小题，每小题4分，共16分）‎ ‎13、秦九韶是我国南宋时期的数学家，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图1所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，x的值分别为4，2，则输出v的值为 .‎ ‎14. 的展开式中项的系数为 .‎ ‎15．用0，1，2，3，4这五个数字组成无重复数字的五位数，其中恰有一个偶数数字夹在两个奇数数字之间的五位数的个数是_________.‎ ‎16. 甲、乙、丙、丁、戊五位同学站成一排照相留念，要求甲乙均不与丙相邻，有______________种不同排法。‎ 三、解答题 （17 题10分， 18~22题每题12分.解答应写出文字说明）‎ ‎ 17、在区间内任取两个数（可以相等），分别记为和，‎ ‎(1)若、为正整数，求这两数中至少有一个偶数的概率；‎ ‎(2)若、，求、满足的概率.‎ ‎18.（1）若 的展开式中第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项的系数；‎ ‎（2）（a+x）（1+x）4的展开式中x的奇数次幂项的系数之和为32，求a的值．‎ ‎19.由四个不同的数字1，2，4，x组成无重复数字的三位数．                                         ‎ ‎（1）若x=5，其中能被5整除的共有多少个？                                         ‎ ‎（2）若x=9，其中能被3整除的共有多少个？                                         ‎ ‎（3）若x=0，其中的偶数共有多少个？                                         ‎ ‎（4）若所有这些三位数的各位数字之和是252，求x．                                        ‎ ‎ 20.一台机器使用时间较长，但还可以使用．它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器运转的速度而变化，如表为抽样试验结果：‎ 转速x（转/秒）‎ ‎16‎ ‎14‎ ‎12‎ ‎8‎ 每小时生产有缺点的零件数y（件）‎ ‎11‎ ‎9‎ ‎8‎ ‎5‎ ‎（1）用相关系数r对变量y与x进行相关性检验；‎ ‎（2）如果y与x有线性相关关系，求线性回归方程；‎ ‎（3）若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么，机器的运转速度应控制在什么范围内？（结果保留整数）‎ 参考数据：xiyi=438，t=m2﹣1，yi2=291，≈25.62．‎ 参考公式：相关系数计算公式：‎ r = =‎ 回归方程=x+中斜率和截距的最小二乘估计公式分别为： =﹣．‎ ‎21．（本小题满分12分）‎ 如图，图②为图①空间图形的主视图和侧视图，其中侧视图为正方形．在图①中，设平面BEF与平面ABCD相交于直线l．‎ ‎（Ⅰ）求证：l⊥面CDE；‎ A B C D E F 图①‎ ‎1‎ ‎1‎ ‎1‎ 图②‎ 主视图 侧视图 ‎1‎ ‎（Ⅱ）在图①中，线段DE上是否存在点M，使得直线MC与平面BEF所成角的正弦值等于？若存在，求出点M的位置；若不存在，请说明理由．‎ ‎22..淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比学|科网，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg）某频率直方图如下：‎ 旧养殖方法 新养殖方法 ‎（1）设两种养殖方法的箱产量相互独立，记A表示事件：旧养殖法的箱产量低于‎50kg, 新养殖法的箱产量不低于‎50kg,估计A的概率；‎ ‎（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：‎ 箱产量＜‎‎50kg 箱产量≥‎‎50kg 旧养殖法 新养殖法 ‎（3）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01），对两种养殖方法的优劣进行比较。‎ ‎ ‎ 沫若中学 高二下期 ‎2016级半期考试数学(理)试卷 参考答案 A；2、C 3、D；4、D 5、B； 6、B； 7、C 8、A 9、D 10、A 11、C 12、 A ‎13、66 14、 - 6 15、28‎ ‎ ‎ ‎16.36‎ ‎17、解：(1)当为正整数，同时抛掷两枚骰子，等可能性的基本事件共36个，如下：‎ ‎、、、、、； 、、、、、；‎ ‎、、、、、； 、、、、、；‎ ‎、、、、、； 、、、、、.‎ 记“两个数中至少有一个为偶数”为事件A，包含上述基本事件的个数为27，由古典概型可知. 分 当时，记事件总体为，所求事件为B，则有，‎ ‎ B：，对应的区域为正方形，其面积为 ‎，B对应的区域为四分之一圆，其面积为，由几何概型可知. 分 ‎18.解：（1）由题意可得+=2，解得n=7 或n=14．‎ 当n=7时，展开式中二项式系数最大的项是T4和T5．‎ ‎∴T4 的系数为••23=，T5的系数为••24=70，‎ 当n=14时，展开式中二项式系数最大的项是T8 ．‎ ‎∴T8的系数为••27=3432． 分 ‎（2）设f（x）=（a+x）（1+x） = a0+a1x+a2x2+…+a5x5，‎ 令x=1，则=a0+a1+a2+…+a5 = f（1）=16（a+1）…①，‎ 令x=﹣1，则f（﹣1）=a0﹣a1+a2+…+﹣a5=0，②，‎ ‎①﹣②得，2（a1+a3+a5）=16（a+1），‎ 根据题意可得2×32=16（a+1）， ∴a=3． 分 ‎19.解：（1）若x=5，则四个数字为1，2，4，5；                                         ‎ 又由要求的三位数能被5整除，则5必须在末尾，                                         ‎ 在1、2、4三个数字中任选2个，放在前2位，有=6种情况，                                         ‎ 即能被5整除的三位数共有6个；                                         ‎ ‎（2）若x=9，则四个数字为1，2，4，9；                                         ‎ 又由要求的三位数能被3整除，则这三个数字为1、2、9或2、4、9，                                         ‎ 取出的三个数字为1、2、9时，有=6种情况，                                         ‎ 取出的三个数字为2、4、9时，有=6种情况，                                         ‎ 则此时一共有+=12个能被3整除的三位数；                                         ‎ ‎（3）若x=0，则四个数字为1，2，4，0；                                         ‎ 又由要求的三位数是偶数，则这个三位数的末位数字为0或2或4，                                         ‎ 当末位是0时，在1、2、4三个数字中任选2个，放在前2位，有=6种情况，                           ‎ 当末位是2或4时，有××=8种情况，                                        ‎ 此时三位偶数一共有6+8=14个， ‎ 当x=0四个数字最多出现18次，                                        ‎ 所有这些三位数的各位数字之和最大为（1+2+4）×18=126，不合题意，故x=0不成立；                                                  ‎ ‎ 当x≠0时，可以组成无重复三位数共有××=4×3×2=24种，共用了24×3=72    个数字，则每个数字用了=18次，则有252=18×（1+2+4+x），解可得x=7．‎ ‎  20.解　（1）根据表中数据，计算=×（16+14+12+8）=12.5，‎ ‎=×（11+9+8+5）=8.25，‎ ‎4=4×12.5×8.25=412.5，…‎ 所以相关系数r=‎ ‎==≈≈0.995；…‎ 因为r＞0.75，所以y与x有很强的线性相关关系；          …4分 ‎（2）回归方程=x+中， =≈0.7286，‎ ‎=﹣=8.25﹣0.728 6×12.5=﹣0.857 5，‎ ‎∴所求线性回归方程为=0.728 6x﹣0.857 5． …8分 ‎（3）要使≤10，即0.728 6x﹣0.857 5≤10，‎ 解得x≤14.901 9≈15．‎ 所以机器的转速应控制在15转/秒以下．   … …12分 ‎ ‎ ‎  ‎ ‎21．（I）证明：由题意，AD//EF，∵ EF面BEF，AD面BEF，‎ ‎∴ AD//面BEF． ………………………………………………………………2分 又∵ AD面ABCD，面ABCD∩面BEF=l，∴ AD//l，……………3分 由主视图可知，AD⊥CD，由侧视图可知，DE⊥AD，‎ ‎∵ CD∩AD=D，∴ AD⊥面CDE． ∴ l⊥面CDE．………………6分 ‎（II）如图，建立空间直角坐标系D-xyz，‎ 则A(1，0，0)，B(1，1，0)，C(0，2，0)，E(0，0，1)，F(1，0，1)，‎ ‎∴ =(1，0，0)，=(0，-1，1)，……7分 A B C D E F x y z M 设面BEF的一个法向量n=(x，y，z)，‎ 则由·n=0，·n=0可得 ‎ 令y=1，则z=1，‎ ‎∴ n=(0，1，1)， …………………………9分 设M(0，0，m)，则=(0，2，-m)，‎ ‎∴ cos<，n>=，解得m=或m=6（舍），‎ 即存在满足点M，此时M的位置在线段DE的处（靠近E点）．……12分 ‎   解：（Ⅰ）f(旧)=0.012×5+0.014×5+0.024×5+0.034×5+0.040×5=0.62，‎ f(新）=（0.068+0.046+0.010+0.008）×5=0.66，‎ 由于两种养殖方法的箱产量相互独立，‎ 于是P（A）=0.62×0.66=0.4092---------3分 ‎（Ⅱ）旧养殖法的箱产量低于‎50kg的有100×0.62=62箱，不低于‎50kg的有38箱，新养殖法的箱产量不低于‎50kg的有100×0.66=66箱，低于‎50kg的有34箱，得到2×2列联表如下：‎ ‎ ‎ 箱产量<‎‎50kg 箱产量≥‎‎50kg 合计 旧养殖法 ‎62‎ ‎38‎ ‎100‎ 新养殖法 ‎34‎ ‎66‎ ‎100‎ 合计 ‎96‎ ‎104‎ ‎200‎ 所以 ‎，所以有99%的把握认为箱产量与养殖方法有关。----------7分 ‎（III）根据箱产量的频率分布直方图，新养殖法的箱产量不低于‎50kg的频率为0.038×5+0.046×5+0.010×5+0.008×5=0.66>0.50，不低于‎55kg的频率为0.046×5+0.010×5+0.008×5=0.32<0.50，于是新养殖法箱产量的中位数介于‎50kg到‎55kg之间，设新养殖法箱产量的中位数为x，则有（55-x）×0.068+0.046×5+0.010×5+0.008×5=0.50 ，解得x=52. 3529‎ 因此，新养殖法箱产量的中位数的估计值52. 35。-------10分 ‎ ‎ 比较：旧的中位数，平均数都在‎45kg至‎50kg之间，新的 中位数，平均数都是‎52.35kg,，新箱产量分布集中在程度比旧的高（众数），可以断定：新养殖法的箱产量较高且稳定，所以新养殖法优于旧养殖法。------12分   ‎