- 2021-06-23 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习立体几何中的平行和垂直学案(江苏专用)
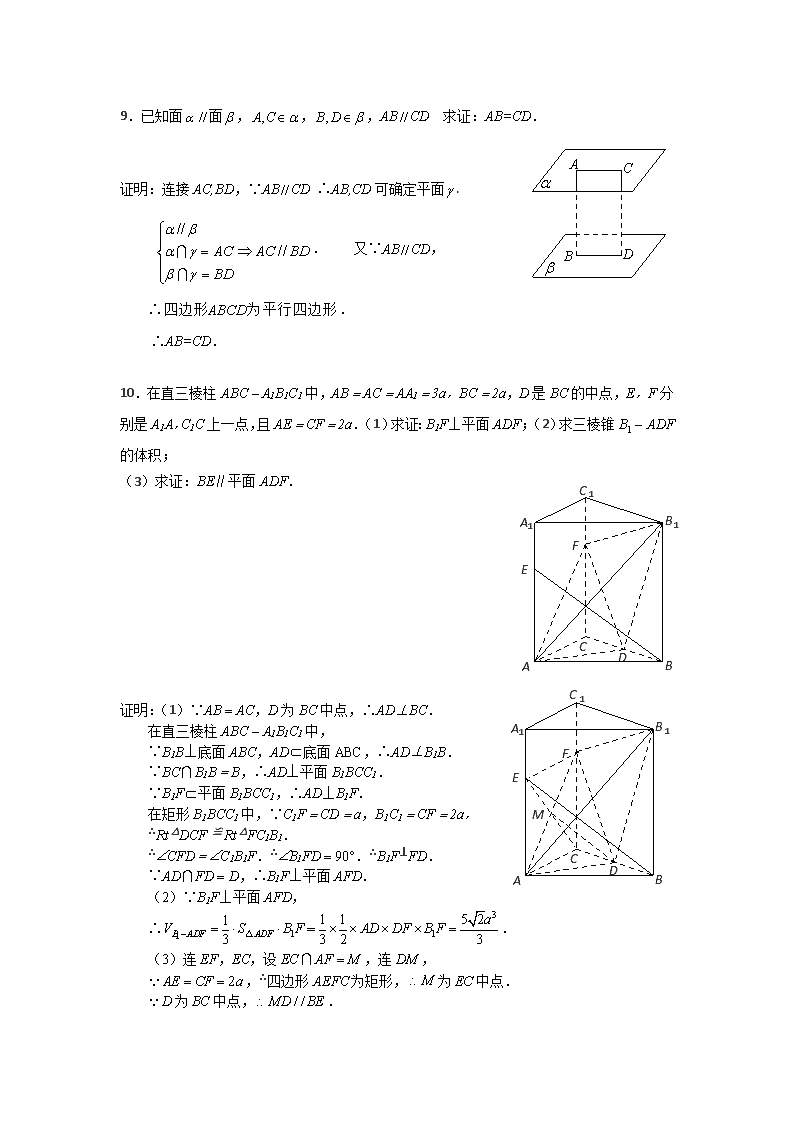
热点问题6 立体几何中的平行和垂直 一、填空题 1. 设为两两不重合的平面,m,n,l为两两不重合的直线,给出下列命题: (1)若;(2)若; (3)若;(4)若 其中真命题是__________ 答案:(3) (4) 2.如图,是平面的斜线段,为斜足.若点在平 面 内运动,使得的面积为定值,则动点的轨迹是__________. (填“圆”“椭圆”“一条直线”“两条平行直线”) 答案:椭圆 解析:考虑到三角形面积为定值,底边一定,从而P到直线AB的距离为定值,若忽略平面的限制,则P轨迹类似为以AB为轴的圆柱面,加上后者平面,轨迹为圆柱面与平面的交集,轨迹为椭圆。 3.棱长为a的正四面体(侧棱长等于底面边长的正三棱锥)ABCD的四个顶点均在同一个球面上,则此球的半径R=________. 答案:a 解析:相关组合体的转化和计算,借助球内接正方体 4.如图,已知三棱锥A—BCD的底面是等边三角形,三条侧棱长都等于1,且∠BAC=30°,M、N分别在棱AC和AD上,则 BM+MN+NB的最小值为 . 答案: 解析:多面体(旋转体)表面上两点间的最短路径与展开图将三棱锥A—BCD的侧面沿AB“展开”在同一平面上. 5.正三棱锥中,,,分别是棱上的点,为边的中点,,则三角形的面积为 . 答案: 解析:由为边的中点得,又得且交于点,另由,可求得为 的中点,从而,则的面积为。 6.已知三棱锥的所有顶点都在球的球面上,是边长为的正三角形,为球的直径,且;则此棱锥的体积为 . 答案: 解析: 的外接圆的半径,点到面的距离,为球的直径点到面的距离为, 此棱锥的体积为. 7.设m、n是异面直线,则 (1)一定存在平面,使m⊂且n∥; (2)一定存在平面,使m⊂且n⊥; (3)一定存在平面γ,使m、n到γ的距离相等; (4)一定存在无数对平面与,使m⊂,n⊂,且∥. 上述4个命题中正确命题的序号为________. 答案:(1)(3) 8.已知正四棱锥中,,那么当该棱锥的体积取最大时,高为 . 答案:2 解析:考察锥体的体积,考察函数的最值问题.设底面边长为a,则高所以,设,则,当y取最值时,,解得或时,体积最 大,此时 二、解答题 9.已知面面,,,ABCD 求证:AB=D C B A CD. 证明:连接AC,BD,∵ABCD ∴AB,CD可确定平面. . 又∵ABCD, ∴. ∴AB=CD. 10.在直三棱柱ABC - A1B1C1中,AB = AC = AA1 = 3a,BC = 2a,D是BC的中点,E,F分别是A1A,C1C上一点,且AE = CF = 2a.(1)求证:B1F⊥平面ADF;(2)求三棱锥B1 - ADF的体积; A F C B D C B 1 1 1 E 1 1 1 A (3)求证:BE∥平面ADF. A F C B D C B 1 1 1 E 1 1 1 A M 证明:(1)∵AB = AC,D为BC中点,∴AD⊥BC. 在直三棱柱ABC - A1B1C1中, ∵B1B⊥底面ABC,AD底面ABC,∴AD⊥B1B. ∵BCB1B = B,∴AD⊥平面B1BCC1. ∵B1F平面B1BCC1,∴AD⊥B1F. 在矩形B1BCC1中,∵C1F = CD = a,B1C1 = CF = 2a, ∴Rt△DCF ≌ Rt△FC1B1. ∴ÐCFD = ÐC1B1F.∴ÐB1FD = 90°.∴B1F⊥FD. ∵ADFD = D,∴B1F⊥平面AFD. (2)∵B1F⊥平面AFD, ∴=. (3)连EF,EC,设,连, ,∴四边形AEFC为矩形,为中点. 为中点,. 平面,.平面,平面 11.如图,平面PAC平面ABC,ACBC,PECB,M是AE的中点. (1)若N是PA的中点,求证:平面CMN平面PAC; (2)若MN平面ABC,求证:N是PA的中点. N M E P C B A 证明(1)∵平面PAC平面ABC, 平面PAC平面ABC=AC, ACBC, 平面ABC ∴BC平面PAC ∵M是AE的中点, N是PA的中点 ∴MNPE 又∵PEBC ∴MNBC ∴MN平面PAC 又∵MN平面CMN ∴平面CMN平面PAC (2)设平面PAE平面ABC=l 又∵MN平面ABC, MN平面PAE ∴MNl ∵PEBC, PE平面ABC,BC平面ABC ∴PE平面ABC ∵PE平面PAE, 平面PAE平面ABC=l ∴PEl ∴PEMN ∵M是AE的中点 ∴N是PA的中点. 12.如图,在直三棱柱ABCA1B1C1中,ACBC,CC1= 4,是棱CC1上的一点. (1)求证:BCAM ; (2)若N是AB的中点,且CN∥平面,求CM的长. C 【解】(1)因为是直三棱柱,所以平面, 因为平面,所以. 因为,,平面,所以平面. C 图1 因为平面,所以. (2)证法一:如图1,取的中点,连结,. 因为是的中点,所以, 因为,所以,所以与共面. 因为∥平面,平面平面,所以. C 图2 所以四边形为平行四边形,所以 证法二:如图2,设与确定的平面交于点, 连结,. 因为∥平面,平面, 平面平面,所以. 因为,平面,平面,所以平面. 又平面,平面平面,所以, Q C 图3 所以,所以四边形为平行四边形.因为是的中点, 所以. 证法三:如图3,取的中点, 连结,. 因为是的中点,所以, 因为平面,平面,所以平面. 因为CN∥平面,,平面, 所以平面平面. 因为平面平面,平面平面, 所以. 因为,所以四边形是平行四边形, 所以. 证法四:如图4,分别延长,设交点为S,连结AC. C 图4 因为∥平面,平面, 平面平面, 所以∥AS.由于AN=NB,所以BC=CS. 又因为∥,同理可得,, 所以. 查看更多