- 2021-06-23 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年河南省镇平县第一高级中学高二3月月考数学(文)试题 Word版
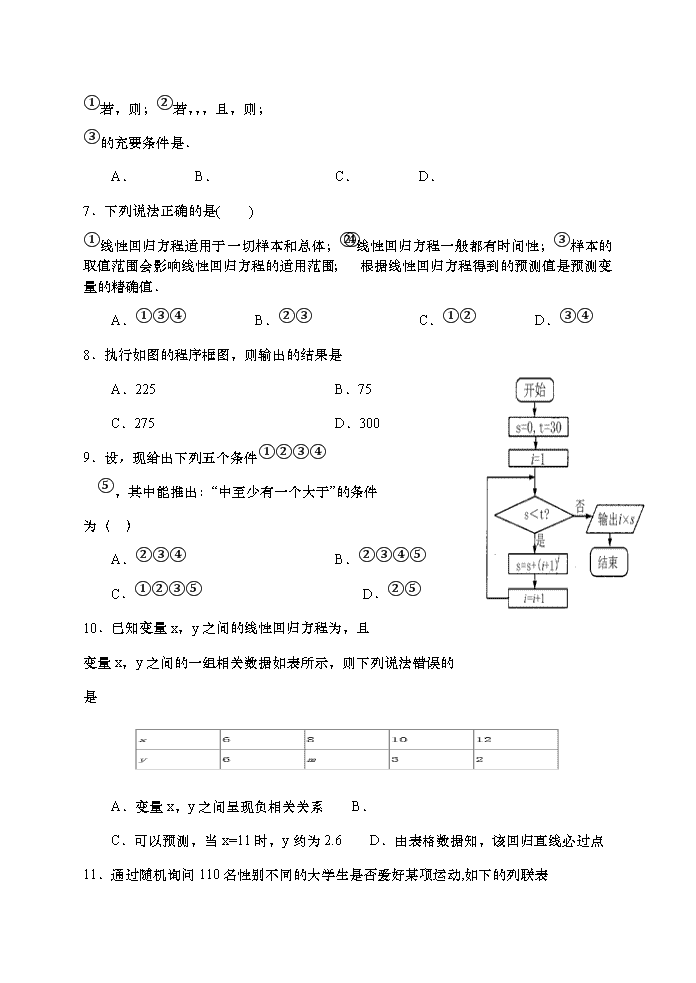
河南省镇平县第一高级中学2018-2019学年高二3月月考文科数学试题 第I卷(选择题) 一、单选题 1.i为虚数单位,则的虚部为 A.2 B. C.2i D. 2. 观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…, 则a7+b7=( ) A.18 B.29 C.47 D.76 3. 如图所示,半径为1的圆O是正方形MNPQ的内切圆,将一颗豆子随机地扔到正方形MNPQ内,用A表示事件“豆子落在圆O内”,B表示事件“豆子落在扇形阴影部分内”,则 A. B. C. D. 4.某商场为了了解毛衣的月销售量(件)与月平均气温之间的关系, 随机统计了某个月的月销售量与当月平均气温,其数据如下表: 月平均气温 月销售量(件) 由表中数据算出线性回归方程中的,气象部门预测下个月的平均气温约为,据此估计该商场下个月毛衣销售量约为( )件 . A. B. C. D. 5.一同学打出若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前2012个圈中的●的个数是 ( ) A. B. C. D. 6.下列命题中,,为复数,则正确命题的个数是( ) ①若,则;②若,,,且,则; ③的充要条件是. A. B. C. D. 7.下列说法正确的是( ) ①线性回归方程适用于一切样本和总体;②线性回归方程一般都有时间性;③样本的取值范围会影响线性回归方程的适用范围;④根据线性回归方程得到的预测值是预测变量的精确值. A.①③④ B.②③ C.①② D.③④ 8.执行如图的程序框图,则输出的结果是 A.225 B.75 C.275 D.300 9.设,现给出下列五个条件①②③④ ⑤,其中能推出:“中至少有一个大于”的条件 为( ) A. ②③④ B.②③④⑤ C.①②③⑤ D.②⑤ 10.已知变量x,y之间的线性回归方程为,且 变量x,y之间的一组相关数据如表所示,则下列说法错误的 是 A.变量x,y之间呈现负相关关系 B. C.可以预测,当x=11时,y约为2.6 D.由表格数据知,该回归直线必过点 11.通过随机询问110名性别不同的大学生是否爱好某项运动,如下的列联表 由列联表算得,得到的正确结论是( ) A.在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别有关” B.在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别无关” C.在犯错误的概率不超过0.001的前提下,认为“爱好该项运动与性别有关” D.在犯错误的概率不超过0.001的前提下,认为“爱好该项运动与性别无关” 12.将正整数排成下表:则在表中,数字2017出现在( ) A.第44行第80列 B.第45行第81列 C.第44行第81列 D.第45行第80列 第II卷(非选择题) 二、填空题 13.若复数(i为虚数单位,a>0)满足,则a=_______. 14.古埃及发现如下有趣等式:,,,,,按此规律,______ 15.一个算法的程序框图如图所示,若该程序输出的结果为,则判断框中的条件中的整数的值是_______________. 16.设函数 ,观察: , , , ,……根据以上事实,由归纳推理可得: 当且时,=__________. 三、解答题 17.复数,为虚数单位m为实数若在复平面内对应的点位于第四象限,求m的取值范围; (2) 若,为虚数,且,求实数m,n的值. 18.已知x∈R,a=x2-1,b=2x+2. (1)求a+b的取值范围; (2)用反证法证明:a,b中至少有一个大于等于0. 19.已知函数 (1)由, ,,这几个函数值,你能发现与有什么关系?并证明你的结论; (2)求的值; 20.在内蒙古自治区超级汽车文化赛事娱乐综合体.为了减少对环境的污染,某环保部门租用了特制环保车清洁现场垃圾.通过查阅近5年英雄会参会人数(万人)与沙漠中所需环保车辆数量(辆),得到如下统计表: 参会人数(万人) 11 9 8 10 12 所需环保车辆(辆) 28 23 20 25 29 (1)根据统计表所给5组数据,求出关于的线性回归方程. (2)已知租用的环保车平均每辆的费用(元)与数量(辆)的关系为 .根据实际参会人数为所需要投入使用的环保车,每辆支付费用6000元,超出实际需要的车辆,主办方不支付任何费用.预计本次英雄会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测环保部门在确保清洁任务完成的前提下,应租用多少辆环保车?获得的利润是多少?(注:利润主办方支付费用租用车辆的费用).参考公式: 21.已知,求证: (1);(2). 22.某中学举行讲座,从参加讲座的男生中随机抽取了50人,女生中随机抽取了70人参加VR知识测试,成绩分成优秀和非优秀两类,统计两类成绩人数得到如下的列联表: 优秀 非优秀 总计 男生 a 35 50 女生 30 d 70 总计 45 75 120 (1)确定a,d的值; (2)试判断能否有90%的把握认为VR知识的测试成绩优秀与否与性别有关; (3)从该校测试成绩获得优秀的同学中按性别采用分层抽样的方法,随机选出6名组成宣传普及小组.现从这6人中随机抽取2名到校外宣传,求“到校外宣传的2名同学中至少有1名是男生”的概率.附: P(K2≥k0) 0.25 0.15 0.10 0.05 0.025 0.010 k0 1.323 2.072 2.706 3.841 5.024 6.635 2019.3.17-18高二月考文科数学试题 参考答案 1.B 2.B 3.B 4.A 5.C 6.A 7.B 8.D 9.D 10.B 11.A 12.B 13.1 14. 15.6 16. 17. 18. 19. 20. 21. 22. 查看更多