2018中考数学试题分类：考点20 等腰三角形、 等边三角形和直角三角形

2018中考数学试题分类：考点20 等腰三角形、 等边三角形和直角三角形

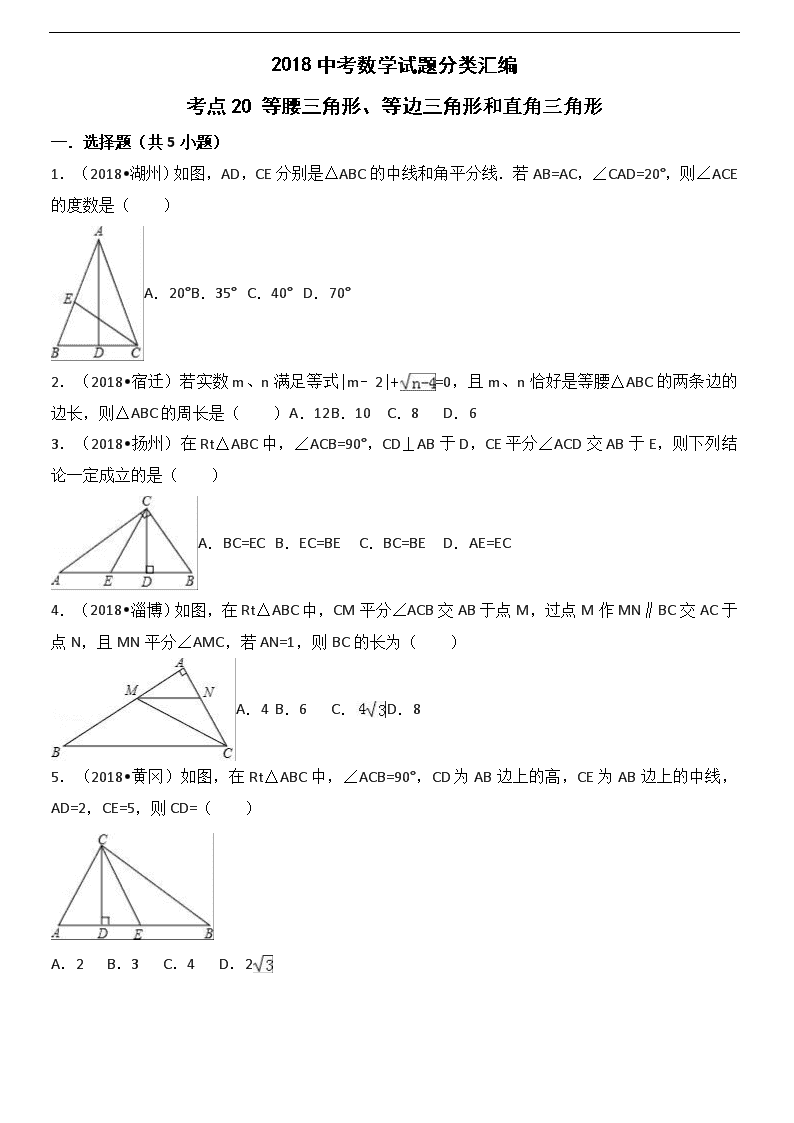
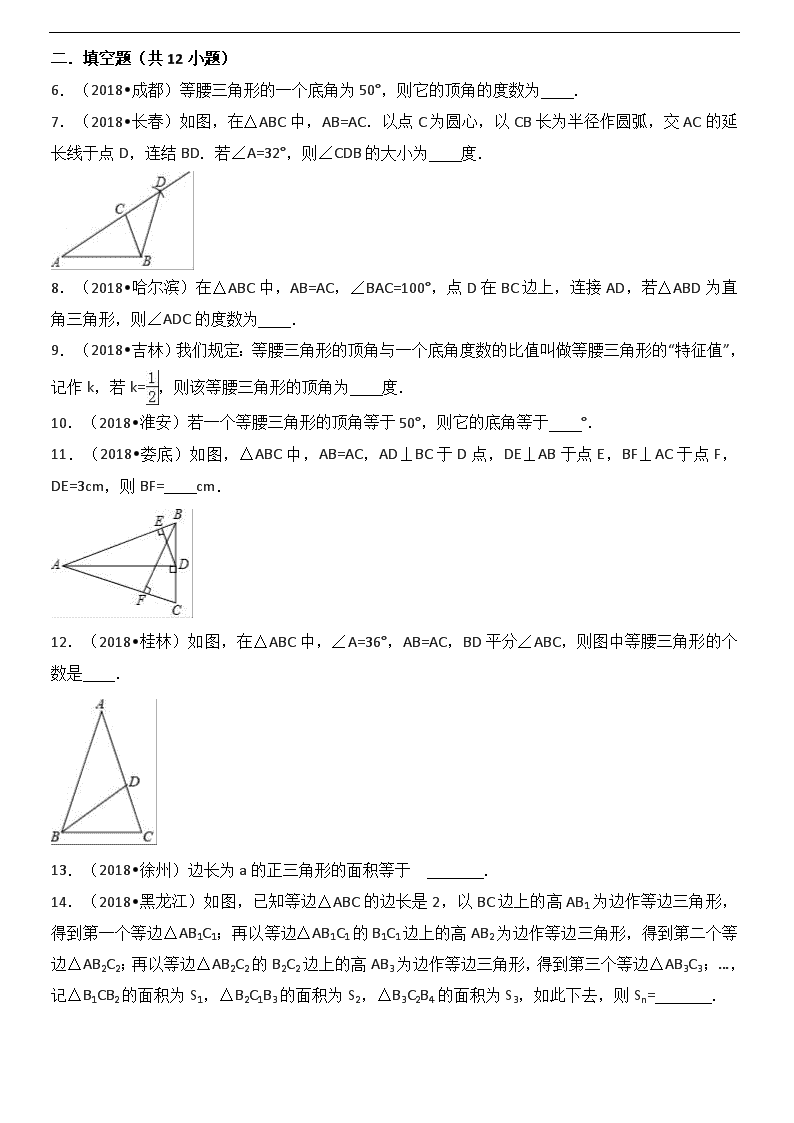
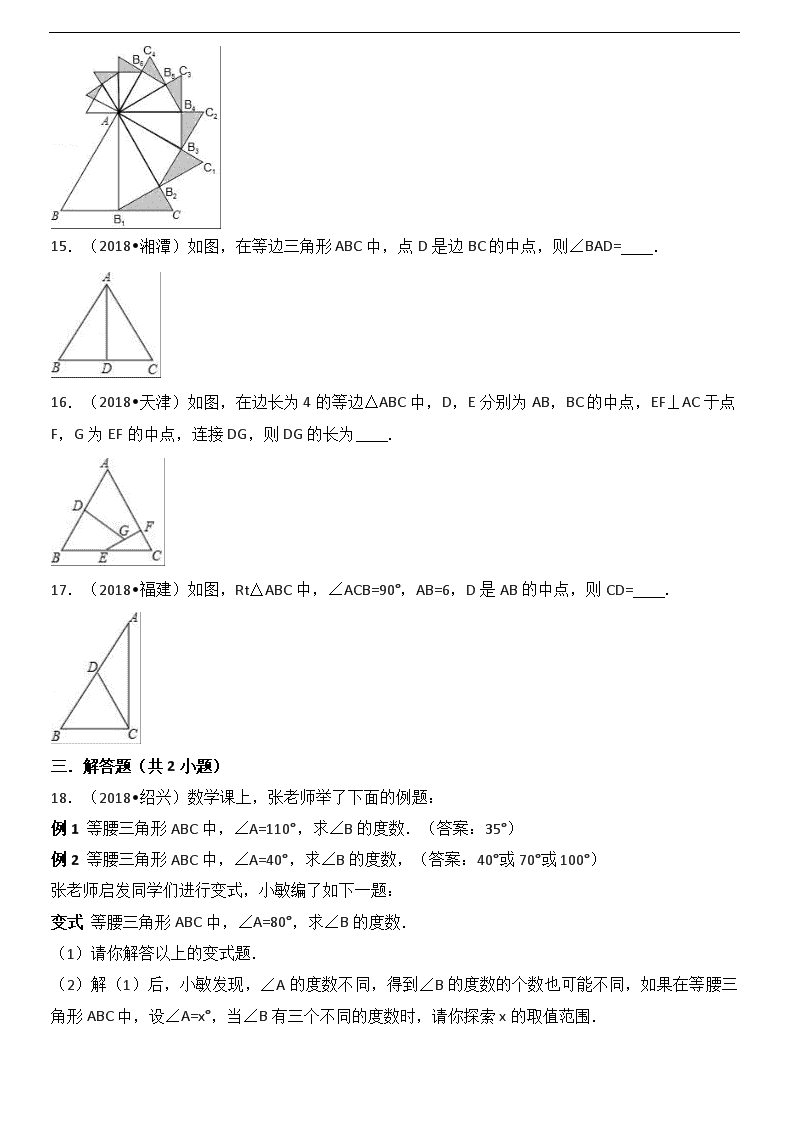
‎2018中考数学试题分类汇编 考点20 等腰三角形、等边三角形和直角三角形 一．选择题（共5小题）‎ ‎1．（2018•湖州）如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（　　）‎ A．20° B．35° C．40° D．70°‎ ‎2．（2018•宿迁）若实数m、n满足等式|m﹣2|+=0，且m、n恰好是等腰△ABC的两条边的边长，则△ABC的周长是（　　）A．12 B．10 C．8 D．6‎ ‎3．（2018•扬州）在Rt△ABC中，∠ACB=90°，CD⊥AB于D，CE平分∠ACD交AB于E，则下列结论一定成立的是（　　）‎ A．BC=EC B．EC=BE C．BC=BE D．AE=EC ‎4．（2018•淄博）如图，在Rt△ABC中，CM平分∠ACB交AB于点M，过点M作MN∥BC交AC于点N，且MN平分∠AMC，若AN=1，则BC的长为（　　）‎ A．4 B．6 C． D．8‎ ‎5．（2018•黄冈）如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，CE为AB边上的中线，AD=2，CE=5，则CD=（　　）‎ A．2 B．3 C．4 D．2‎ ‎　‎ 二．填空题（共12小题）‎ ‎6．（2018•成都）等腰三角形的一个底角为50°，则它的顶角的度数为　　．‎ ‎7．（2018•长春）如图，在△ABC中，AB=AC．以点C为圆心，以CB长为半径作圆弧，交AC的延长线于点D，连结BD．若∠A=32°，则∠CDB的大小为　　度．‎ ‎8．（2018•哈尔滨）在△ABC中，AB=AC，∠BAC=100°，点D在BC边上，连接AD，若△ABD为直角三角形，则∠ADC的度数为　　．‎ ‎9．（2018•吉林）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为　　度．‎ ‎10．（2018•淮安）若一个等腰三角形的顶角等于50°，则它的底角等于　　°．‎ ‎11．（2018•娄底）如图，△ABC中，AB=AC，AD⊥BC于D点，DE⊥AB于点E，BF⊥AC于点F，DE=3cm，则BF=　　cm．‎ ‎12．（2018•桂林）如图，在△ABC中，∠A=36°，AB=AC，BD平分∠ABC，则图中等腰三角形的个数是　　．‎ ‎13．（2018•徐州）边长为a的正三角形的面积等于 　．　‎ ‎14．（2018•黑龙江）如图，已知等边△ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边△AB1C1；再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边△AB2C2；再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形，得到第三个等边△AB3C3；…，记△B1CB2的面积为S1，△B2C1B3的面积为S2，△B3C2B4的面积为S3，如此下去，则Sn=　 　．‎ ‎15．（2018•湘潭）如图，在等边三角形ABC中，点D是边BC的中点，则∠BAD=　　．‎ ‎16．（2018•天津）如图，在边长为4的等边△ABC中，D，E分别为AB，BC的中点，EF⊥AC于点F，G为EF的中点，连接DG，则DG的长为　　．‎ ‎17．（2018•福建）如图，Rt△ABC中，∠ACB=90°，AB=6，D是AB的中点，则CD=　　．‎ 三．解答题（共2小题）‎ ‎18．（2018•绍兴）数学课上，张老师举了下面的例题：‎ 例1 等腰三角形ABC中，∠A=110°，求∠B的度数．（答案：35°）‎ 例2 等腰三角形ABC中，∠A=40°，求∠B的度数，（答案：40°或70°或100°）‎ 张老师启发同学们进行变式，小敏编了如下一题：‎ 变式 等腰三角形ABC中，∠A=80°，求∠B的度数．‎ ‎（1）请你解答以上的变式题．‎ ‎（2）解（1）后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同，如果在等腰三角形ABC中，设∠A=x°，当∠B有三个不同的度数时，请你探索x的取值范围．‎ ‎19．（2018•徐州）（A类）已知如图，四边形ABCD中，AB=BC，AD=CD，求证：∠A=∠C．‎ ‎（B类）已知如图，四边形ABCD中，AB=BC，∠A=∠C，求证：AD=CD．‎