广东省汕头市2019届高三第二次模拟考试（B卷）理科数学（PDF版）

广东省汕头市2019届高三第二次模拟考试（B卷）理科数学（PDF版）

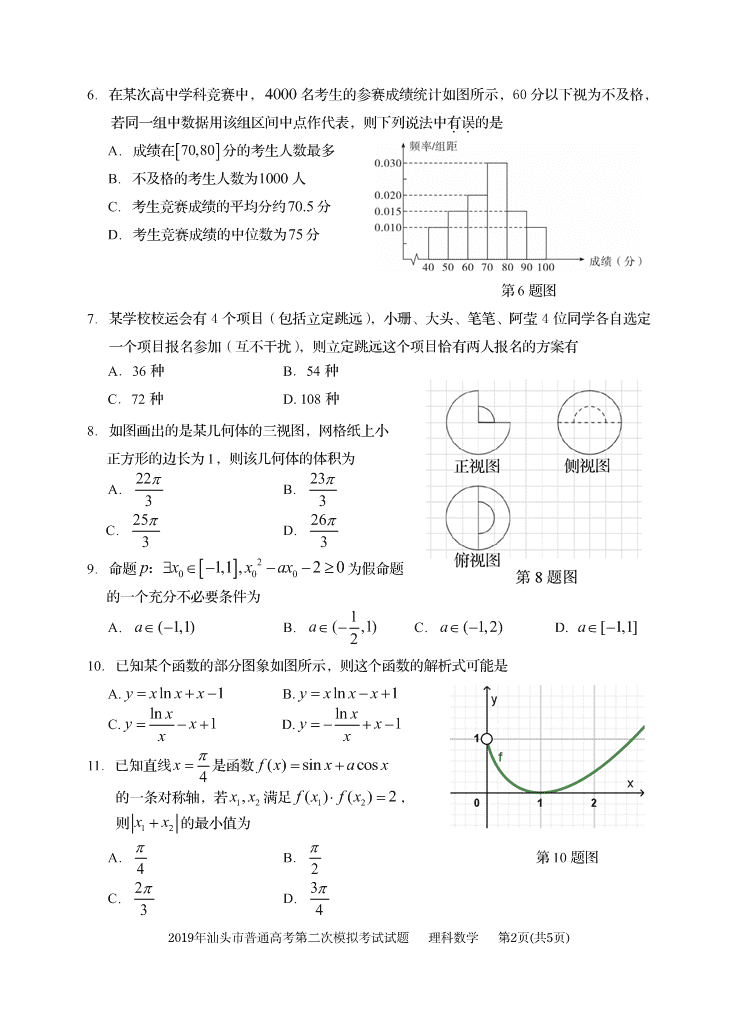
2019年汕头市普通高考第二次模拟考试试题 理科数学 第1页(共5页) 秘密★启用前 试卷类型：B 2019年汕头市普通高考第二次模拟考试试题 理 科 数 学 本试卷5页，23小题，满分150分。考试用时120分钟。 注意事项：1．答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。 用2B铅笔将试卷类型填涂在答题卡相应位置上。将条形码横贴在答题卡右上角 “条形码粘贴处”。 2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答 案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其它答案。答案不能答在 试卷上。 3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指 定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案； 不准使用铅笔和涂改液。不按以上要求作答无效。 4．考生必须保持答题卡的整洁。考试结束后，将试卷和答题卡一并交回。 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是 符合要求的。 1．设集合 { 1,0,1,2}A  ，集合 { | 2 , }xB y y x R   ，则 AB＝ A．{0，1} B．{1，2} C．{0，1，2} D．（0，+∞） 2．已知复数 1 34zi ， 2z t i，且 12zz 是实数，则实数t 等于 A． 3 4 B． 4 3 C． 4 3 D． 3 4 3．记 nS 为等差数列{}na 的前 n 项和，若 1 1a  ， 3 4 222S a S ，则 8a  A．8 B．9 C．16 D．15 4．已知向量 a ， b 的夹角为 2  ，且  2, 1a ， 2b ，则 2ab A． 23 B．3 C． 21 D． 41 5．已知 ABC 的周长为12，且  2,0A  ，  2,0B ，则顶点C 的轨迹方程为 A． 22 421( 0)xy y   B． 22 421( 0)xy y   C． 22 16 12 1( 0)xy y   D． 22 16 12 1( 0)xy y   2019年汕头市普通高考第二次模拟考试试题 理科数学 第2页(共5页) 6．在某次高中学科竞赛中， 4000 名考生的参赛成绩统计如图所示，60 分以下视为不及格， 若同一组中数据用该组区间中点作代表，则下列说法中有误．．的是 A．成绩在 70,80 分的考生人数最多 B．不及格的考生人数为1000 人 C．考生竞赛成绩的平均分约70.5 分 D．考生竞赛成绩的中位数为75分 第 6 题图 7．某学校校运会有 4 个项目（包括立定跳远），小珊、大头、笔笔、阿莹 4 位同学各自选定 一个项目报名参加（互不干扰），则立定跳远这个项目恰有两人报名的方案有 A．36 种 B．54 种 C．72 种 D. 108 种 8．如图画出的是某几何体的三视图，网格纸上小 正方形的边长为 1，则该几何体的体积为 A． 22 3  B． 23 3  C． 25 3  D． 26 3  9．命题   2 0 0 01,1 , 2 0p x x ax     ： 为假命题 的一个充分不必要条件为 A． ( 1,1)a B． 1( ,1)2a C． ( 1,2)a D. [ 1,1]a 10．已知某个函数的部分图象如图所示，则这个函数的解析式可能是 A. ln 1y x x x   B. ln 1y x x x   C. ln 1xyxx   D. ln 1xyxx    11．已知直线 4x  是函数 ( ) sin cosf x x a x 的一条对称轴，若 12,xx满足 12( ) ( ) 2f x f x， 则 12xx 的最小值为 A． 4  B． 2  第 10 题图 C． 2 3  D． 3 4  2019年汕头市普通高考第二次模拟考试试题 理科数学 第3页(共5页) 12．若 120 x x a   都有 2 1 1 2 1 2ln lnx x x x x x   成立，则 a 的最大值为 A． 1 2 B．1 C．e D． 2e 二、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13．设变量 x 、 y 满足约束条件 5 24 1 0 xy xy yx y       ，则目标函数 32z x y的最大值为______. 14．已知双曲线C ： 22 221( 0, 0)xy ab ab     的左、右焦点为 1F 、 2F ，过 1F 且斜率为 2 2 的 直线l 与 的一条渐近线在第一象限相交于 A 点，若 21AF AF ，则该双曲线的离心率为 _______. 15．记 nS 为数列{}na 的前 n 项和，若 2 3S  ， 1 1nnaS  ，则通项公式 na  ______． 16．长方体 1 1 1 1ABCD A B C D 中， 11, 2, 3AB AD AA   ， P 是棱 1DD 上的动点，则 1PAC 的面积最小时， 1 DP PD  _______． 三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17～21 题为必考题， 每个试题考生都必须作答。第 22、23 题为选考题，考生根据要求作答。 (一)必考题：共 60 分。 17．(本小题满分 12 分) ABC 的内角 ,,A B C 的对边分别为 ,,abc，已知 2 2 3( cos )b c a B ． (1)求 cos A； (2)过点 A 作 AD AB 交 BC 的延长线于 D ，若 3CD  ， 23AD AC ，求 ACD 的 面积. 18．(本小题满分 12 分) 如图，等边三角形 PAC 所在平面与梯形 ABCD 所在平面互相垂直，且有 //AD BC ， 2AB AD DC   ， 4BC  . (1)证明：平面 PAB 平面 PAC ； (2)求二面角 B PC D的余弦值. 第 18 题图 *()nN 2019年汕头市普通高考第二次模拟考试试题 理科数学 第4页(共5页) 19．(本小题满分 12 分) 已知抛物线 D ： 2 4xy ，过 x 轴上一点 E （不同于原点）的直线l 与抛物线 交于两点 11( , )A x y ， 22( , )B x y ，与 y 轴交于C 点. (1)若 1EA EC ， 2EB EC ，求乘积 1 · 2 的值； (2)若 (4,0)E ，过 A ， B 分别作抛物线 的切线，两切线交于点 M ，证明：点 在定直 线上，求出此定直线方程. 20．(本小题满分 12 分) 某工厂 ,AB两条相互独立的生产线生产同款产品，在产量一样的情况下通过日常监控得 知， 生产线生产的产品为合格品的概率分别为 p 和21p  (0.5 1)p． (1)从 生产线上各抽检一件产品，若使得至少有一件合格的概率不低于99.5%，求 的最小值 0p ． (2)假设不合格的产品均可进行返工修复为合格品，以（1）中确定的 作为 p 的值． ①已知 生产线的不合格品返工后每件产品可分别挽回损失 5 元和 3 元，若从两条生 产线上各随机抽检 1000 件产品，以挽回损失的平均数为判断依据，估计哪条生产线的挽回损 失较多？ ②若最终的合格品（包括返工修复后的合格品）按照一、二、三等级分类后，每件可分 别获利 10 元、8 元、6 元，现从 生产线的最终合格品中各随机抽取 100 件进行检测，结果统计如右图： 用样本的频率分布估计总体分 布，记该工厂生产一件产品的利润为 X ，求 的分布列并估计该厂产量 2000 件时利润的期望值． 第 20 题图 2019年汕头市普通高考第二次模拟考试试题 理科数学 第5页(共5页) 21．(本小题满分 12 分) 已知函数 () xf x e ax a   ( aR ). (1)讨论函数 ()fx的极值； (2)设 12,xx是 的两个零点，证明： 120xx. (二)选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题 记分。 22．(本小题满分 10 分)选修 4－4：坐标系与参数方程 在直角坐标系中 xOy 中，曲线C 的参数方程为 cos 3 sin   xa ya   （ 为参数， 0a  ）. 以 坐 标 原 点 为 极 点 ， x 轴正半轴为极轴建立极坐标系，已知直线l 的 极 坐 标 方 程 为 cos( ) 2 24 . (1)求曲线C 的普通方程和直线 l 的直角坐标方程； (2)设 P 是曲线C 上的一个动点，若点 到直线 的距离的最大值为32，求 a 的值． 23．(本小题满分10分)选修4－5：不等式选讲 已知函数 ( ) 2 2 1f x x x    ． (1)在右图的坐标系中画出 y = ()fx的图象； (2)若 = 的最小值为 m ，当正数 ,ab 满足 21mba时，求 2ab 的最小值． 第 23 题图 高效冲刺用《高考数学必备题型手册》 第1页(共6页) 理科数学参考答案和评分标准 一．选择题 二．填空题 13. 6 14. 3 15. 12n na  16. 1 4 17. 解：（1）由正弦定理得： 2 2 sin 3(sin sin cos )B C A B …………………………1 分 3(sin( ) sin cos )A B A B   …………………………2 分 3(sin cos cos sin sin cos )A B A B A B   …………………………3 分 3cos sinAB …………………………4 分 (0, )A Q sin 0,A........................5 分 22cos 3A…………………………6 分 （2）如图， 2 1sin 1 cos 3BAC BAC     …………………………7 分 1cos sin 3CAD BAC    ……………8 分 设 3AD x ，则 2AC x ，在 ACD 中，由余弦定理，得 229 4 9 2 2 3 cosx x x x CAD       …………………………9 分 解得 1x  ，即 3, 2AD AC，…………………………10 分 1 2 3 sin2ACDS CAD      ………………………11 分 1 2 22 3 2 223     …………………………12 分 18.（1）证明：取 BC 中点 M ，连接 AM 则四边形 AMCD 为菱形，即有 1 2AM MC BC ，…1 分 所以 AB AC ………………………2 分 AB Q 平面 ABCD 平面 ABCD  平面 PAC 平面 ABCDI 平面 PAC AC …………3 分 AB平面 PAC ………………………4 分 又 AB  平面 PAB 平面 PAB 平面 PAC ………………………5 分 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B A D C C D B C B B B B 高效冲刺用《高考数学必备题型手册》 第2页(共6页) （2）由（1）可得 23AC  取 AC 中点O ，连接 PO ，则 ,3PO AC PO………………………6 分 PO Q 平面 PAC 平面 PAC 平面 ABCD 平面 PAC I 平面 ABCD AC PO平面 ABCD………………………7 分 以 A 为原点建系如图，则 (2,0,0),B ， (0, 3,3)P ， (0,2 3,0)C ， ( 1, 3,0)D  ，………………………8 分 ( 2,2 3,0)BC  uuur ， (0, 3, 3)PC  uuur ， ( 1, 3,0)CD    uuur 设平面 BPC 的法向量为 1 ( , , )n x y z ur ，则 2 2 3 0 3 3 0 xy yz     ，取 1z  ，得 1 (3, 3,1)n  ur ………………………9 分 设平面 PCD的法向量为 2 ( , , )n x y z uur ，则 30 3 3 0 xy yz     ，取 ，得 1 ( 3, 3,1)n  ur ………………………10 分 1 21 2 1 2 9 3 1 5cos , 13| || | 13 13 nnnn nn          r uurr uur r uur ………………………11 分 二面角 B PC D的余弦值为 5 13 ………………………12 分 19.解析：（1）设 ( ,0)Et 0t  ， (0, )Cm，......................1 分 由 1 2 EA EC EB EC      uuur uuur uuur uuur 得 1 1 1 2 2 2 ( , ) ( , ) ( , ) ( , ) x t y t m x t y t m          ，.....................2 分 解得 1 1 2 2 tx t tx t       ......................3 分 设直线l 的斜率为 k ，其方程为 ()y k x t， 高效冲刺用《高考数学必备题型手册》 第3页(共6页) 由 2 () 4 y k x t xy    得 2 4 4 0x kx kt   ，......................4 分 16 ( ) 0k k t   时，设 11( , )A x y 22( , )B x y 1 2 1 24 , 4x x k x x kt    ，......................5 分 所以 2 2 1 2 1 2 12 22 () 441t x x t x x t kt kt tt       ......................6 分 （2）设 ( , )M x y ， 由 2 4xy 得 2 4 xy  ，所以 2 xy  .......................7 分 所以在 2 1 1( , )4 xAx 处的切线方程为 2 11 1()42 xxy x x   ，即 2 11 24 x x xy ， 同理在 2 2 2( , )4 xBx 的切线方程为 2 22 24 x x xy ，......................8 分 由 2 11 2 22 24 24 x x xy x x xy     得 12 12 2 4 xxx xxy     ，......................9 分 因为 (4,0)E ，即 4t  ......................10 分 所以由（1）得， 1 2 1 24 , 16x x k x x k    ，所以 2 4 xk yk    ，......................11 分 所以得 2yx ，即交点 在直线 上.......................12 分 20. 解：（1）设从 ,AB生产线上各抽检一件产品，至少有一件合格为事件C ， 设从 生产线上抽检到合格品分别为事件 ,MN，则 互为独立事件……1 分 由已知有 ()P M p ， ( ) 2 1P N p且(0.5 1)p，则   2 ( ) 1 ( ) 1 ( ) ( ) 1 (1 ) 1 (2 1) 1 2(1 ) P C P M N P M P N p p p               ……………………………2 分 令 21 2(1 ) 0.995p   ，即 2(1 ) 0.0025p ，解得 0.95p  ……………………3 分 故 p 的最小值 0 0.95p  ． ……………………………4 分 （2）由（1）可知 生产线生产的产品为合格品的概率分别为0.95和0.9 高效冲刺用《高考数学必备题型手册》 第4页(共6页) 即 ,AB生产线的不合格品率分别为0.05和0.1 ……………………………5 分 ①解法 1： 设从 生产线上各随机抽检 1000 件产品，抽到的不合格品件数分别为 12,XX， 则 1 ~ (1000 , 0.05)XB ， 2 ~ (1000 , 0.1)XB ……………………………6 分 所以 生产线挽回损失的平均数分别为 1(5 ) 5 1000 0.05 250EX    （元）， 2(3 ) 3 1000 0.1 300EX    （元）……7 分 则 12(5 ) (3 )E X E X ，估计 B 线挽回的平均损失较多．…………………………8 分 ①解法 2： 由已知， A 生产线上随机抽检 1000 件产品， 估计有不合格品1000 0.05 50（件），可挽回损失：50 5 250 （元）；……6 分 生产线上随机抽检 1000 件产品， 估计有不合格品1000 0.1 100 （件），可挽回损失：100 3 300 （元）……7 分 则估计 线挽回的平均损失较多． …………………………8 分 ②由已知， 10, 8, 6X  ，用样本的频率分布估计总体分布，则 20 35 11( 10) 200 40PX    ， 60 40 1( 8) 200 2PX    ， 20 25 9( 6) 200 40PX    …………………………10 分 X 的分布列为 X 10 8 6 P 11 40 1 2 9 40 …………………………11 分 ∴ 11 1 9 81( ) 10 8 6 8.140 2 40 10EX         （元） 故估计该厂产量 2000 件时利润的期望值为 2000 8.1 16200 （元）．…………12 分 21. 解：（1） ()fx的定义域为( , )  又 / () xf x e a ①当 0a  时，在( , )  上， / ( ) 0fx ， ()fx是增函数， ()fx无极値； ②当 0a  时， / ( ) 0fx 得 lnxa 在 ( ,ln )a 上， / ( ) 0fx ， ()fx是减函数； 在 (ln , )a  上， / ( ) 0fx ， ()fx是增函数， 高效冲刺用《高考数学必备题型手册》 第5页(共6页) 所以当 lnxa 时， ()fx取得极小值 (ln ) ln lnf a a a a a a a     ，无极大值； 综合知：①当 0a  时， ()fx无极値； ②当 0a  时， ()fx有极小值 (ln ) lnf a a a ，无极大值； （2）设 12,xx是 ()fx的两个零点，则 0a  即 12,xx是方程 ( ) 0fx 的根 所以 12,xx是方程 11 x x ae  的根 令 1() x xhx e  即 12,xx是函数 ()hx 与 1y a 图像的交点的横坐标 又 / 2 ( 1)( ) 0 xx xx e x e xhx ee      ，得 0x  在 ( ,0) 上 / ( ) 0hx ， ()hx 是增函数；在(0, ) 上 / ( ) 0hx ， ()hx 是减函数， 所以：当 0x  时， ()hx 取得极大値 (0) 1h  又当 1x  时， ( ) 0hx  ； 1x  时， ( ) 0hx 要使得函数 与 图像有两个交点，则 101a 则 1a  且 1210xx    120xx 210xx    ，且 101x   要证 120xx，即证 1 2 1 1( ) ( ) ( )h x h x h x a    又 12 1 1 1 1( ) ( ) (1 ) 1 0xh x h x x e x       令 2( ) (1 ) 1( 1 0)xk x x e x x       即证： ( ) 0kx / 2 2 2( ) 2(1 ) 1 (1 2 ) 1x x xk x e x e x e        令 /2( ) ( ) (1 2 ) 1xm x k x x e    / 2 2 2( ) 2 2(1 2 ) 4x x xm x e x e xe      在 ( 1,0) 上 / ( ) 0mx ， ()mx是增函数，所以 /( ) ( ) (0) 0m x k x m   ，则 ()kx是减 函数，所以 ( ) (0) 0k x k成立 所以 120xx成立. 22. 解：（1）依题意得曲线C 的普通方程为 22 2213xy aa ，.......................2分 因为 cos( ) 2 24 所以 cos sin 4    ，...................................3分 因为 cosx  ， siny  ，...................................4分 所以直线l 的直角坐标方程为 4xy 即 40  xy ，........................5分 高效冲刺用《高考数学必备题型手册》 第6页(共6页) （2）设点 ( cos , 3 sin )P a a，则点 P 到直线l 的距离 cos 3 sin 4 2   aa d ...................................7分 2 sin( ) 46 2   a  ...................................8分 因为 0a ，所以当sin( ) 16   时， max 2432 2 ad ，......................9分 所以 1a ............................................................................10 分 23. 解：（1） 3 1, 1, ( ) 3, 1 1, 3 1, 1. xx f x x x xx            ()y f x 的图像如图所示．..............................................5分 （2）由（1）知 min( ) ( 1) 2  f x f ，所以 2m .........................6 分 所以 1 2 12 ( 2 )( )2   a b a b ba..............................................7 分 5 2  ab ba ..............................................8 分 592 22   ab ba ..............................................9 分 当且仅当 ab ba即 2 3ab 时等号成立， 所以 2ab 的最小值为 9 2 . ..............................................10 分 姓 名 考生号 考场号 座位号 选 择 题 答 题 区 5 [A] [B] [C] [D] 6 [A] [B] [C] [D] 7 [A] [B] [C] [D] 8 [A] [B] [C] [D] 二、填空题 13． 14． 15． 16． 三、解答题 17.（本小题满分 12 分） 2019 年汕头市普通高考第二次模拟考试——理科数学答题卡 试卷类型 试卷 A 试卷 B 以下为非选择题答题区，必须用黑色字迹的钢笔或签字笔在指定区域内按题号顺序作答，否则答案无效。 注意事项： 1.在“条形码粘贴处”横贴条形码，注意不要超 出框外。 2.答题前考生务必用黑色字迹的钢笔或签字笔 填写姓名、考生号、考场号和座位号。 3.用 2B 铅笔填涂信息点，正确方法是■。信息 点框内必须涂满、涂黑，否则无效；修改时须 用橡皮擦干净。 4.考生必须根据监考员所发试卷的类型正确填 涂试卷类型信息点，否则答案无效。 5.作答时注意题号顺序，不得擅自更改题号。 6.作答选做题时，须将选做的试题号所对应的信 息点涂黑，漏涂、错涂、多涂的，答案无效。 7.保持卡面清洁，不要折叠和弄破。 9 [A] [B] [C] [D] 10 [A] [B] [C] [D] 11 [A] [B] [C] [D] 12 [A] [B] [C] [D] 条形码粘贴处 （请核对条形码上的考生号和姓名） 第 1 面 （共 6 面） 第Ⅰ卷 选择题 第Ⅱ卷 非选择题 监考员填涂缺考 [ ] 1 [A] [B] [C] [D] 2 [A] [B] [C] [D] 3 [A] [B] [C] [D] 4 [A] [B] [C] [D] 18.（本小题满分 12 分） 请勿在此处作任何标记或作答 第 2 面 （共 6 面） 姓 名 考生号 考场号 座位号 19.（本小题满分 12 分） 第 3 面 （共 6 面） 2019 年汕头市普通高考第二次模拟考试——理科数学答题卡 条形码粘贴处 （请核对条形码上的考生号和姓名） 监考员填涂缺考 [ ] 注意事项： 1.在“条形码粘贴处”横贴条形码，注意不要超 出框外。 2.答题前考生务必用黑色字迹的钢笔或签字笔 填写姓名、考生号、考场号和座位号。 3.作答选做题时，须将选做的试题号所对应的信 息点涂黑，漏涂、错涂、多涂的，答案无效。 4.保持卡面清洁，不要折叠和弄破。 20.（本小题满分 12 分） 第 4 面 （共 6 面） 请勿在此处作任何标记或作答 姓 名 考生号 考场号 座位号 21.（本小题满分 12 分） 第 5 面 （共 6 面） 2019 年汕头市普通高考第二次模拟考试——理科数学答题卡 请勿在此处作任何标记或作答 条形码粘贴处 （请核对条形码上的考生号和姓名） 监考员填涂缺考 [ ] 注意事项： 1.在“条形码粘贴处”横贴条形码，注意不要超 出框外。 2.答题前考生务必用黑色字迹的钢笔或签字笔 填写姓名、考生号、考场号和座位号。 3.用 2B 铅笔填涂信息点，正确方法是 ■。信息 点框内必须涂满、涂黑，否则无效；修改时须 用橡皮擦干净。 4.作答时注意题号顺序，不得擅自更改题号。 5.作答选做题时，须将选做的试题号所对应的信 息点涂黑，漏涂、错涂、多涂的，答案无效。 6.保持卡面清洁，不要折叠和弄破。 选考题 请从第 22、23 两题中任选一题作答，并用 2B 铅笔将所选题目对应的题号右侧方框涂黑，按所涂题号进行 评分；多涂、多答，按所涂的首题进行评分；不涂，按本选考题的首题进行评分． （本小题满分 10 分） 我所选择的题号是 22 题 23 题 第 6 面 （共 6 面） 请勿在此处作任何标记或作答