- 2021-06-23 发布 |
- 37.5 KB |
- 14页

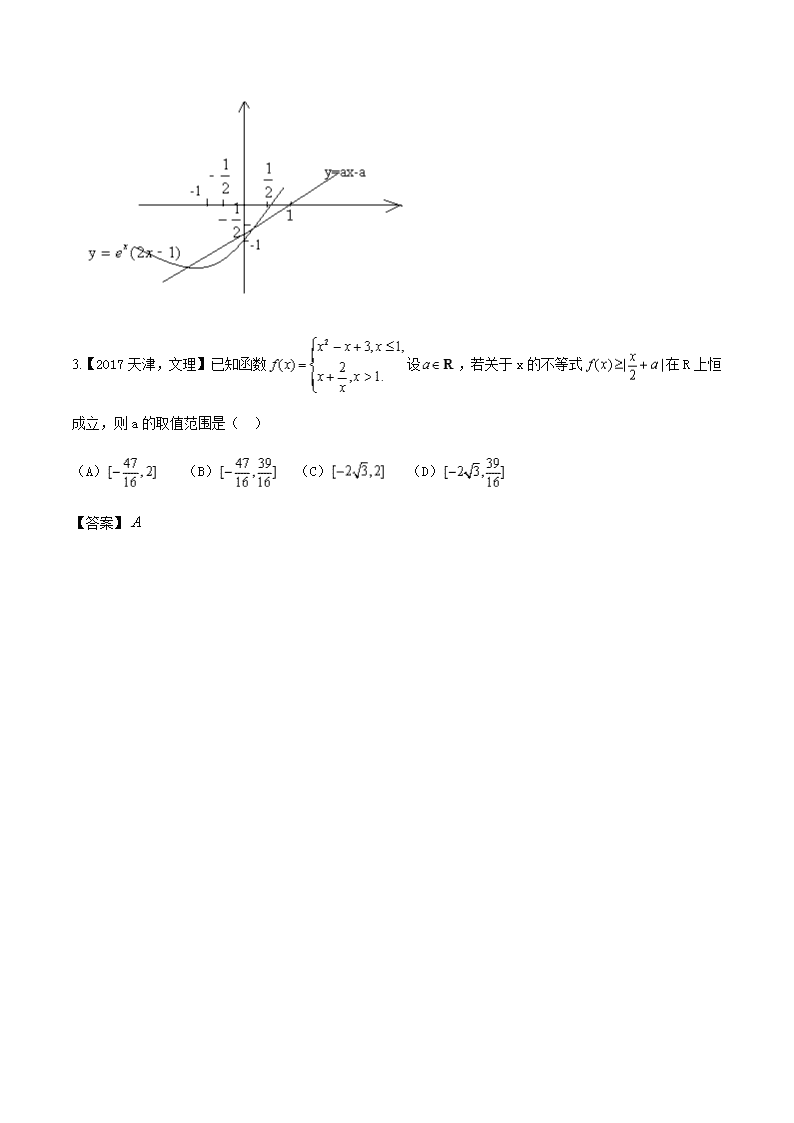

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题2-4+函数、不等式中恒成立问题(练)-2018年高考数学(文)二轮复习讲练测
2018 高三二轮复习之讲练测之练案【新课标版文科数学】 1. 练高考 1.【2014 山东高考】已知实数 yx, 满足 )10( aaa yx ,则下面关系是恒成立的是( ) A. 1 1 1 1 22 yx B. )1ln()1(ln 22 yx C. yx sinsin D. 33 yx 【答案】 D 【解析】由 (0 1)x ya a a 及指数函数的性质得, ,x y 所以, 3 3x y ,选 D . 2.【2015 高考新课标 1】设函数 ( )f x = (2 1)xe x ax a ,其中 a 1,若存在唯一的整数 0x ,使得 0( )f x 0, 则 a 的取值范围是( ) (A)[- 3 2e ,1) (B)[- 3 2e , 3 4 ) (C)[ 3 2e , 3 4 ) (D)[ 3 2e ,1) 【答案】D 3.【2017 天津,文理】已知函数 2 3, 1, ( ) 2 , 1. x x x f x x xx 设 a R ,若关于 x 的不等式 ( ) | |2 xf x a 在 R 上恒 成立,则 a 的取值范围是( ) (A) 47[ ,2]16 (B) 47 39[ , ]16 16 (C)[ 2 3,2] (D) 39[ 2 3, ]16 【答案】 A 4.【2017 天津,文 19】设 ,a bR ,| | 1a .已知函数 3 2( ) 6 3 ( 4)f x x x a a x b , ( ) e ( )xg x f x . (Ⅰ)求 ( )f x 的单调区间; (Ⅱ)已知函数 ( )y g x 和 exy 的图象在公共点(x0,y0)处有相同的切线, (i)求证: ( )f x 在 0x x 处的导数等于 0; (ii)若关于 x 的不等式 ( ) exg x 在区间 0 0[ 1, 1]x x 上恒成立,求 b 的取值范围. 【答案】(Ⅰ)递增区间为 ( , )a ,(4 , )a ,递减区间为 ( ),4a a .(2)(ⅰ) ( )f x 在 0x x 处的导 数等于 0.(ⅱ)b 的取值范围是[ 7 ],1 . 【解析】 所以 0 00 0 0 0 0 ( )e e e ( ( ) ( )) ex x x x f f f x 'x x ,解得 0 0 ( ) 1 ( ) 0 f ' x xf . 所以, ( )f x 在 0x x 处的导数等于 0. (ii)因为 ( ) exg x , 0 0[ 1 1],x x x ,由 e 0x ,可得 ( ) 1f x . 又因为 0( ) 1f x , 0( ) 0f ' x ,故 0x 为 ( )f x 的极大值点,由(I)知 0x a . 另一方面,由于| | 1a ,故 1 4a a , 由(I)知 ( )f x 在 ( , )1a a 内单调递增,在 ( ), 1a a 内单调递减, 5.【2016 高考江苏卷】已知函数 ( ) ( 0, 0, 1, 1)x xf x a b a b a b .设 12, 2a b . (1)求方程 ( ) 2f x 的根; (2)若对任意 x R ,不等式 (2 ) f( ) 6f x m x 恒成立,求实数 m 的最大值; (3)若 0 1, 1a b > ,函数 2g x f x 有且只有 1 个零点,求 ab 的值。 【答案】(1)①0 ②4(2)1 【解析】 (1)因为 12, 2a b ,所以 ( ) 2 2x xf x . ①方程 ( ) 2f x ,即 2 2 2x x ,亦即 2(2 ) 2 2 1 0x x , 所以 2(2 1) 0x ,于是 2 1x ,解得 0x . ②由条件知 2 2 2 2(2 ) 2 2 (2 2 ) 2 ( ( )) 2x x x xf x f x . 因为 (2 ) ( ) 6f x mf x 对于 x R 恒成立,且 ( ) 0f x , 所以 2( ( )) 4 ( ) f xm f x 对于 x R 恒成立. 而 2( ( )) 4 4 4( ) 2 ( ) 4( ) ( ) ( ) f x f x f xf x f x f x ,且 2( (0)) 4 4(0) f f , 所以 4m ,故实数 m 的最大值为 4. (2)因为函数 ( ) ( ) 2g x f x 只有 1 个零点,而 0 0(0) (0) 2 2 0g f a b , 所以 0 是函数 ( )g x 的唯一零点. 若 0 0x ,同理可得,在 0 2 x 和 log 2a 之间存在 ( )g x 的非 0 的零点,矛盾. 因此, 0 0x . 于是 ln 1ln a b ,故 ln ln 0a b ,所以 1ab . 2.练模拟 1. 已知函数 2 2lnf x ax bx x ( 0a , Rb ),若对任意的 0x ,都有 2f x f 成立,则 ( ) A. ln 1a b B. ln 1a b C. ln 1a b D. ln 1a b 【答案】C 2. 设函数 2 2 2f x ax x ,对于满足1 4x 的一切 x 值都有 0f x ,则实数 a 的取值范围为( ) A. 1a B. 1 12 a C. 1 2a D. 1 2a 【答案】D 【解析】满足1 4x 的一切 x 值,都有 2 2 2 0f x ax x 恒成立,可知 2 2 2 1 1 1 10, 2 4 2 xa a x x ,满足1 4x 的一切 x 值恒成立, 1 1 14 x , 21 1 1 12 0,4 2 2x ,实数 a 的取值范围是 1 ,2 ,实数 a 的取值范围为 1 2a ,故选 D. 3.【2018 届河南省南阳市第一中学高三第六次考】已知函数 3 3 1f x ax x 对 0,1x 总有 0f x 成立,则实数 a 的取值范围是__________. 【答案】[4,+∞) 【解析】当 x∈(0,1]时不等式 ax3-3x+1≥0 可化为 a≥ 3 3 1x x ,设 g(x)= 3 3 1x x ,x∈(0,1],g′(x)= 3 2 6 4 163 3 1 3 2xx x x x x ,因此 g(x)的最大值为 4,则实数 a 的取值范围是[4,+∞). 故答案为[4,+∞) 4.【2018 届高考数学训练】在 R 上定义运算:x*y=x(1-y),若不等式(x-a)*(x+a)≤1 对任意的 x 恒成 立,则实数 a 的取值范围是________. 【答案】 1 3,2 2 【解析】由于(x-a)*(x+a)=(x-a)(1-x-a),则不等式(x-a)*(x+a)≤1 对任意的 x 恒成立,即 x2-x -a2+a+1≥0 恒成立,所以Δ=1-4(-a2+a+1)≤0,解得- 1 2 ≤a≤ 3 2 . 5.【2018 届北京市海淀区高三第一学期期末】对任意实数 k ,定义集合 2 0 , |{ 2 0 , 0 k x y D x y x y x y R kx y . ①若集合 kD 表示的平面区域是一个三角形,则实数 k 的取值范围是______; ②当 0k 时,若对任意的 , kx y D ,有 3 1y a x 恒成立,且存在 , kx y D ,使得 x y a 成 立,则实数 a 的取值范围为_______. 【答案】 1,1 12, 5 平移目标函数 y x a , 当直线和 2y x 重合时,此时 x y 最小,最小值为 2 , 则 2a ,综上所述 a 的取值范围是 12, 5 . 6.【2018 届北京市通州区高三上学期期末】已知函数 ,ln x af x x a R . (Ⅰ)当 0a 时,求函数 f x 的单调区间; (Ⅱ)对任意的 1,x , f x x 恒成立,求 a 的取值范围. 【答案】(Ⅰ)单调递增区间是 ,e ,单调递减区间是 0,1 和 1,e . (Ⅱ) 1.a 3.练原创 1. 三个同学对问题“关于 x 的不等式 2 3 225 5x x x ax 在 1,12 上恒成立,求实数 a 的取值范围”提出 各自的解题思路. 甲说:“只须不等式左边的最小值不小于右边的最大值”. 乙说:“把不等式变形为左边含变量 x 的函数,右边仅含常数,求函数的最值”. 丙说:“把不等式两边看成关于 x 的函数,作出函数图像”. 参考上述解题思路,你认为他们所讨论的问题的正确结论,求 a 的取值范围. 【答案】 10a 【解析】关键在于对甲,乙,丙的解题思路进行思辨,这一思辨实际上是函数思想的反映. 设 2 3 225 5 ,f x x x x g x ax . 甲的解题思路,实际上是针对两个函数的,即把已知不等式的两边看作两个函数, 设 2 3 225 5 ,f x x x x g x ax 其解法相当于解下面的问题: 2. (1)若关于 x 的不等式 02 aaxx 的解集为 ),( ,求实数 a 的取值范围;(2)若关于 x 的不 等式 32 aaxx 的解集不是空集,求实数 a 的取值范围 【答案】(1) 04 a (2) 6a 或 2a . 【解析】(1)设 aaxxxf 2 .则关于 x 的不等式 02 aaxx 的解集为 ),( 0 xf 在 , 上恒成立 0min xf , 即 ,04 4 2 min aaxf 解得 04 a (2)设 aaxxxf 2 .则关于 x 的不等式 32 aaxx 的解集不是空集 3 xf 在 , 上能成立 3min xf , 即 ,34 4 2 min aaxf 解得 6a 或 2a . 3. 若函数 2 6 8y mx mx m 在 R 上恒成立,求 m 的取值范围。 【答案】 0 1m 【解析】要使 2 6 8y mx mx m 在 R 上恒成立,即 2 6 8 0mx mx m 在 R 上 恒成立。 1 0m 时,8 0 0m 成立 2 0m 时, 2 0 36 4 8 32 1 0 m m m m m , 0 1m 由1 , 2 可知, 0 1m 4. 当 (1,2)x 时,不等式 2( 1) logax x 恒成立,求 a 的取值范围. 【答案】1 2a 【解析】 2 1 2: ( ) ( 1) , : ( ) log aT f x x T g x x = 2( 1)x ,则 1T 的图象为右图所示的抛物线,要使对一切 (1,2)x , ( )f x < ( )g x 恒成立即 1T 的图象一定要在 2T 的图象所的下方,显然 1a ,并且必须也只需 (2) (2)g f ,故 log 2 1, 1, 1 2a a a . 5. 设函数是定义在 ( , ) 上的增函数,如果不等式 2(1 ) (2 )f ax x f a 对于任意 [0,1]x 恒成立, 求实数 a 的取值范围. 【答案】 1a 查看更多