- 2021-06-23 发布 |
- 37.5 KB |
- 3页


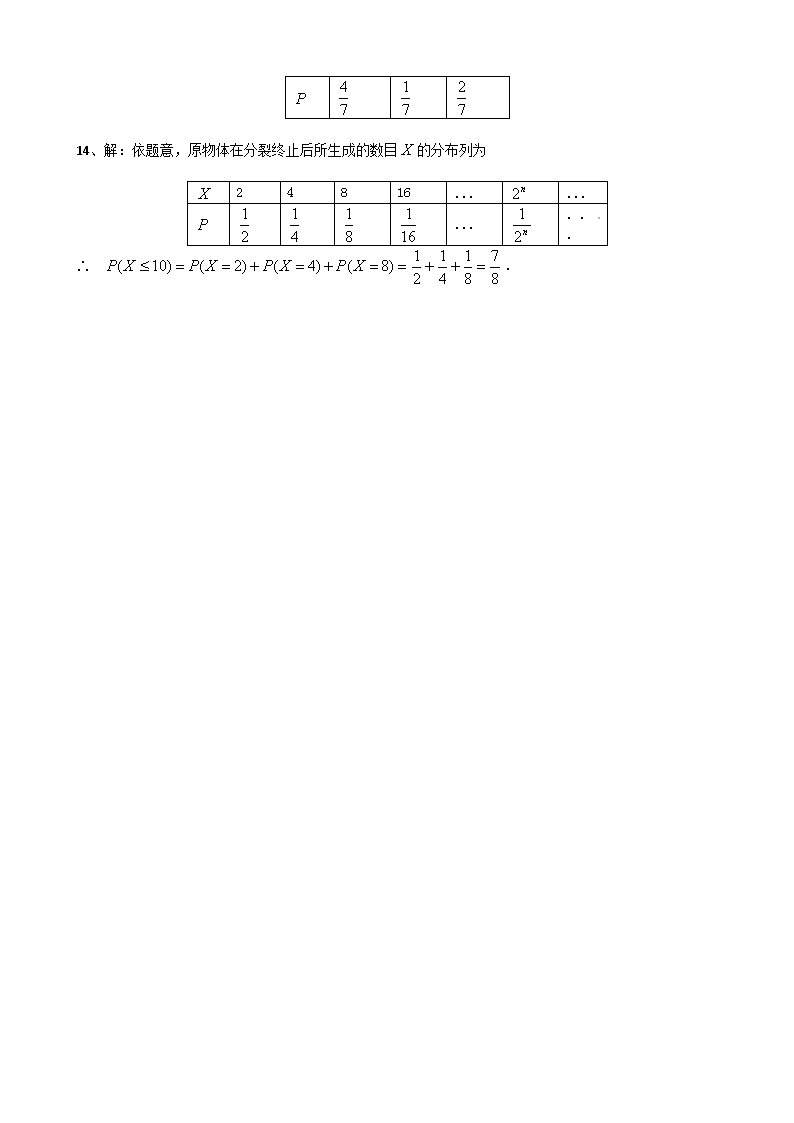
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学:新人教A版选修2-3 2_1离散型随机变量及其分布列(同步练习)
高中数学系列2—3单元测试题(2.1) 一、选择题: 1、如果是一个离散型随机变量,则假命题是( ) A. 取每一个可能值的概率都是非负数; B. 取所有可能值的概率之和为1; C. 取某几个值的概率等于分别取其中每个值的概率之和; D. 在某一范围内取值的概率大于它取这个范围内各个值的概率之和 2①某寻呼台一小时内收到的寻呼次数;②在区间内随机的取一个数;③某超市一天中的顾客量 其中的是离散型随机变量的是( ) A.①; B.②; C.③; D.①③ 3、设离散型随机变量的概率分布如下,则的值为( ) X 1 2 3 4 P A. B. C. D. 4、设随机变量的分布列为,则的值为( ) A.1; B.; C.; D. 5、已知随机变量的分布列为:,,则=( ) A. B. C. D. 6、设随机变量等可能取1、2、3...值,如果,则值为( ) A. 4 B. 6 C. 10 D. 无法确定 7、投掷两枚骰子,所得点数之和记为,那么表示的随机实验结果是( ) A. 一枚是3点,一枚是1点 B. 两枚都是2点 C. 两枚都是4点 D. 一枚是3点,一枚是1点或两枚都是2点 8、设随机变量的分布列为,则的值为( ) A.1; B.; C.; D. 二、填空题: 9 、下列表中能成为随机变量的分布列的是 (把全部正确的答案序号填上) -1 0 1 0.3 0.4 0.4 1 2 3 0.4 0.7 -0.1 5 0 -5 0.3 0.6 0.1 ① ② ③ ④ ⑤ 10、已知为离散型随机变量,的取值为,则的取值为 11、一袋中装有5只同样大小的白球,编号为1,2,3,4,5 现从该袋内随机取出3只球,被取出的球的最大号码数可能取值为 三、解答题: 12、某城市出租汽车的起步价为10元,行驶路程不超出4km,则按10元的标准收租车费若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,他收旅客的租车费可也是一个随机变量 (1)求租车费η关于行车路程ξ的关系式; (2)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟? 13、一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球个数的一半.现从该盒中随机取出一个球,若取出红球得1分,取出黄球得0分,取出绿球得-1分,试写出从该盒中取出一球所得分数的分布列. 分析:欲写出ξ的分布列,要先求出ξ的所有取值,以及ξ取每一值时的概率. 14、一个类似于细胞分裂的物体,一次分裂为二,两次分裂为四,如此继续分裂有限多次,而随机终止.设分裂次终止的概率是(=1,2,3,…).记为原物体在分裂终止后所生成的子块数目,求. 高中数学系列2—3单元测试题(2.1)参考答案 一、选择题: 1、D 2、D 3、C 4、B 5、A 6、C 7、D 8、C 二、填空题: 9、 ③④ 10、 11、 三、解答题: 12、解:(1)依题意得η=2(ξ-4)+10,即η=2ξ+2 (2)由38=2ξ+2,得ξ=18,5×(18-15)=15. 所以,出租车在途中因故停车累计最多15分钟. 13、解:设黄球的个数为,由题意知 绿球个数为,红球个数为,盒中的总数为. ∴ ,,. 所以从该盒中随机取出一球所得分数的分布列为 1 0 -1 14、解:依题意,原物体在分裂终止后所生成的数目的分布列为 2 4 8 16 ... ... ... ... ∴ .查看更多