- 2021-06-23 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2018届湖南省岳阳市岳阳一中高二上学期期中数学试卷(文科)+(解析版)
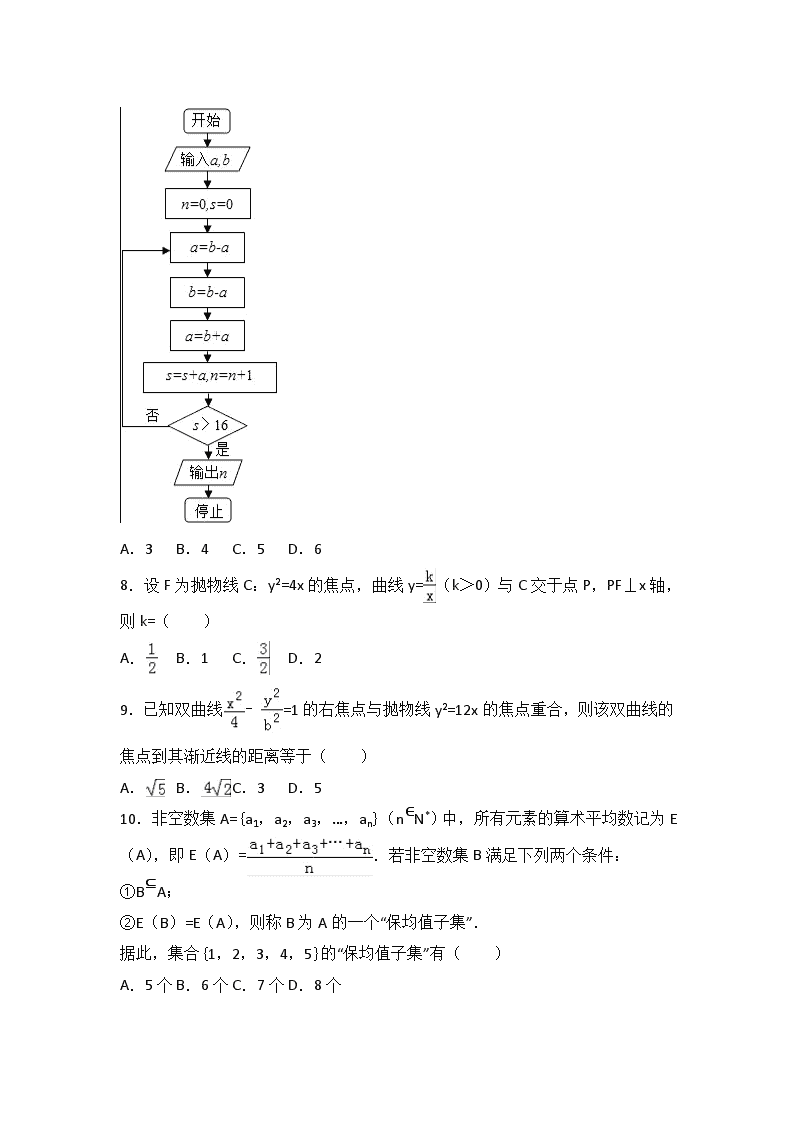
2016-2017学年湖南省岳阳市岳阳一中高二(上)期中数学试卷(文科) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.某年级有1000名学生,随机编号为0001,0002,…,1000,现用系统抽样方法,从中抽出200人,若0122号被抽到了,则下列编号也被抽到的是( ) A.0116 B.0927 C.0834 D.0726 2.命题“∃x0∈(0,+∞),lnx0=x0﹣1”的否定是( ) A.∃x0∈(0,+∞),lnx0≠x0﹣1 B.∃x0∉(0,+∞),lnx0=x0﹣1 C.∀x∈(0,+∞),lnx≠x﹣1 D.∀x∉(0,+∞),lnx=x﹣1 3.已知椭圆的离心率,则实数k的值为( ) A.3 B.3或 C. D.或 4.与直线2x﹣y+4=0的平行的抛物线y=x2的切线方程是( ) A.2x﹣y+3=0 B.2x﹣y﹣3=0 C.2x﹣y+1=0 D.2x﹣y﹣1=0 5.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(1)=( ) A.﹣e B.﹣1 C.1 D.e 6.中心在原点、焦点在x轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( ) A. +=1 B. +=1 C. +=1 D. +=1 7.执行如图程序框图,如果输入的a=4,b=6,那么输出的n=( ) A.3 B.4 C.5 D.6 8.设F为抛物线C:y2=4x的焦点,曲线y=(k>0)与C交于点P,PF⊥x轴,则k=( ) A. B.1 C. D.2 9.已知双曲线﹣=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ) A. B. C.3 D.5 10.非空数集A={a1,a2,a3,…,an}(n∈N*)中,所有元素的算术平均数记为E(A),即E(A)=.若非空数集B满足下列两个条件: ①B⊆A; ②E(B)=E(A),则称B为A的一个“保均值子集”. 据此,集合{1,2,3,4,5}的“保均值子集”有( ) A.5个 B.6个 C.7个 D.8个 11.“a>1”是“函数f(x)=ax﹣2(a>0且a≠1)在区间(0,+∞)上存在零点”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 12.已知双曲线﹣=1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为( ) A. B. C. D. 二、填空题:本大题共5个小题,每小题5分,共20分. 13.已知函数f(x)=,则f(f())的值为 . 14.已知f(x)=x3﹣3x+8,则曲线y=f(x)在点(2,f(2))处的切线斜率为 . 15.在区间[0,9]上随机取一实数x,则该实数x满足不等式1≤log2x≤2的概率为 . 16.过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若,则|AF|= . 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.设,若“a=1”是“A∩B≠Φ”的充分条件,则实数b的取值范围是 . 18.已知双曲线C:﹣=1(a>0,b>0)的离心率为,实轴长为2. (1)求双曲线C的方程; (2)若直线y=x+m被双曲线C截得的弦长为,求m的值. 19.某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组[1,3),第二组[3,5),第三组[5,7),第四组[7,9),第五组[9,11],绘制成如图所示的频率分布直方图. (Ⅰ)求学习时间在[7,9)的学生人数; (Ⅱ)现要从第三组、第四组中用分层抽样的方法抽取6人,从这6人中随机抽取2人交流学习心得,求这2人中至少有1人的学习时间在第四组的概率. 20.已知函数f(x)=x2+(x≠0,a∈R). (1)判断函数f(x)的奇偶性; (2)若f(x)在区间[2,+∞)上是增函数,求实数a的取值范围. 21.已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为F(﹣,0),且右顶点为D(2,0).设点A的坐标是(1,). (1)求该椭圆的标准方程; (2)过原点O的直线交椭圆于点B、C,求△ABC面积的最大值. 22.设函数,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0. (1)求y=f(x)的解析式; (2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值. 2016-2017学年湖南省岳阳市岳阳一中高二(上)期中数学试卷(文科) 参考答案与试题解析 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.某年级有1000名学生,随机编号为0001,0002,…,1000,现用系统抽样方法,从中抽出200人,若0122号被抽到了,则下列编号也被抽到的是( ) A.0116 B.0927 C.0834 D.0726 【考点】系统抽样方法. 【分析】根据系统抽样的定义求出样本间隔即可. 【解答】解:样本间隔为1000÷200=5, 因为122÷5=24余2,故抽取的余数应该是2的号码, 116÷5=23余1,927÷5=185余2,834÷5=166余4,726÷5=145余1, 故选:B. 2.命题“∃x0∈(0,+∞),lnx0=x0﹣1”的否定是( ) A.∃x0∈(0,+∞),lnx0≠x0﹣1 B.∃x0∉(0,+∞),lnx0=x0﹣1 C.∀x∈(0,+∞),lnx≠x﹣1 D.∀x∉(0,+∞),lnx=x﹣1 【考点】命题的否定. 【分析】根据特称命题的否定是全称命题即可得到结论. 【解答】解:命题的否定是:∀x∈(0,+∞),lnx≠x﹣1, 故选:C 3.已知椭圆的离心率,则实数k的值为( ) A.3 B.3或 C. D.或 【考点】椭圆的简单性质. 【分析】当K>5时,由 e===求得K值,当0<K<5时,由 e===,求得K值. 【解答】解:当K>5时,e===,K=. 当0<K<5时,e===,K=3. 综上,K=3,或. 故选 B. 4.与直线2x﹣y+4=0的平行的抛物线y=x2的切线方程是( ) A.2x﹣y+3=0 B.2x﹣y﹣3=0 C.2x﹣y+1=0 D.2x﹣y﹣1=0 【考点】两条直线平行的判定;直线的一般式方程. 【分析】根据切线与直线2x﹣y+4=0的平行,可利用待定系数法设出切线,然后与抛物线联立方程组,使方程只有一解即可. 【解答】解:由题意可设切线方程为2x﹣y+m=0 联立方程组得x2﹣2x﹣m=0 △=4+4m=0解得m=﹣1, ∴切线方程为2x﹣y﹣1=0, 故选D 5.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(1)=( ) A.﹣e B.﹣1 C.1 D.e 【考点】导数的乘法与除法法则;导数的加法与减法法则. 【分析】已知函数f(x)的导函数为f′(x),利用求导公式对f(x)进行求导,再把x=1代入,即可求解; 【解答】解:∵函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+ln x,(x>0) ∴f′(x)=2f′(1)+,把x=1代入f′(x)可得f′(1)=2f′(1)+1, 解得f′(1)=﹣1, 故选B; 6.中心在原点、焦点在x轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( ) A. +=1 B. +=1 C. +=1 D. +=1 【考点】椭圆的简单性质;椭圆的标准方程. 【分析】先根据长轴长为18,且两个焦点恰好将长轴三等分,即可确定椭圆的几何量,从而可求椭圆的方程. 【解答】解:∵长轴长为18 ∴2a=18,∴a=9, 由题意,两个焦点恰好将长轴三等分 ∴2c=×2a=×18=6, ∴c=3, ∴a2=81, ∴b2=a2﹣c2=81﹣9=72, 故椭圆方程为 故选A. 7.执行如图程序框图,如果输入的a=4,b=6,那么输出的n=( ) A.3 B.4 C.5 D.6 【考点】程序框图. 【分析】模拟执行程序,根据赋值语句的功能依次写出每次循环得到的a,b,s,n的值,当s=20时满足条件s>16,退出循环,输出n的值为4. 【解答】解:模拟执行程序,可得 a=4,b=6,n=0,s=0 执行循环体,a=2,b=4,a=6,s=6,n=1 不满足条件s>16,执行循环体,a=﹣2,b=6,a=4,s=10,n=2 不满足条件s>16,执行循环体,a=2,b=4,a=6,s=16,n=3 不满足条件s>16,执行循环体,a=﹣2,b=6,a=4,s=20,n=4 满足条件s>16,退出循环,输出n的值为4. 故选:B. 8.设F为抛物线C:y2=4x的焦点,曲线y=(k>0)与C交于点P,PF⊥x轴,则k=( ) A. B.1 C. D.2 【考点】抛物线的简单性质. 【分析】根据已知,结合抛物线的性质,求出P点坐标,再由反比例函数的性质,可得k值. 【解答】解:抛物线C:y2=4x的焦点F为(1,0), 曲线y=(k>0)与C交于点P在第一象限, 由PF⊥x轴得:P点横坐标为1, 代入C得:P点纵坐标为2, 故k=2, 故选:D 9.已知双曲线﹣=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ) A. B. C.3 D.5 【考点】双曲线的简单性质;抛物线的简单性质. 【分析】确定抛物线y2=12x的焦点坐标,从而可得双曲线的一条渐近线方程,利用点到直线的距离公式,即可求双曲线的焦点到其渐近线的距离. 【解答】解:抛物线y2=12x的焦点坐标为(3,0) ∵双曲线的右焦点与抛物线y2=12x的焦点重合 ∴4+b2=9 ∴b2=5 ∴双曲线的一条渐近线方程为,即 ∴双曲线的焦点到其渐近线的距离等于 故选A. 10.非空数集A={a1,a2,a3,…,an}(n∈N* )中,所有元素的算术平均数记为E(A),即E(A)=.若非空数集B满足下列两个条件: ①B⊆A; ②E(B)=E(A),则称B为A的一个“保均值子集”. 据此,集合{1,2,3,4,5}的“保均值子集”有( ) A.5个 B.6个 C.7个 D.8个 【考点】子集与交集、并集运算的转换;众数、中位数、平均数. 【分析】根据集合A和“保均值子集”的定义把集合的非空真子集列举出来,即可得到个数. 【解答】解:非空数集A={1,2,3,4,5}中,所有元素的算术平均数E(A)==3, ∴集合A的“保均值子集”有:{3},{1,5},{2,4},{3,1,5},{3,2,4},{1,5,2,4},{1,2,3,4,5}共7个; 故选C. 11.“a>1”是“函数f(x)=ax﹣2(a>0且a≠1)在区间(0,+∞)上存在零点”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 【考点】必要条件、充分条件与充要条件的判断. 【分析】我们可以根据充分、充要条件的定义进行判断. ①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件; ②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件; ③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件; ④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件. 【解答】解:∵a>1时,由ax﹣2=0,得x=loga2>0, ∴函数f(x)=ax﹣2(a>0且a≠1)在区间(0,+∞)上存在零点loga2. ∴“a>1”是“函数f(x)=ax﹣2(a>0且a≠1)在区间(0,+∞ )上存在零点”的充分条件; 反之,若函数f(x)=ax﹣2(a>0且a≠1)在区间(0,+∞)上存在零点,则零点为loga2, 由loga2>0,得a>1, ∴“a>1”是“函数f(x)=ax﹣2(a>0且a≠1)在区间(0,+∞)上存在零点”的必要条件. 故选C. 12.已知双曲线﹣=1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为( ) A. B. C. D. 【考点】双曲线的简单性质. 【分析】由双曲线的定义可得|PF1|﹣|PF2|=3|PF2|=2a,再根据点P在双曲线的右支上,|PF2|≥c﹣a,从而求得此双曲线的离心率e的最大值. 【解答】解:∵P在双曲线的右支上, ∴由双曲线的定义可得|PF1|﹣|PF2|=2a, ∵|PF1|=4|PF2|, ∴4|PF2|﹣|PF2|=2a,即|PF2|=a, 根据点P在双曲线的右支上,可得|PF2|=a≥c﹣a,∴a≥c,即e≤, 此双曲线的离心率e的最大值为, 故选:C 二、填空题:本大题共5个小题,每小题5分,共20分. 13.已知函数f(x)=,则f(f())的值为 e . 【考点】函数的值. 【分析】先求出f(),从而求出f(f())的值即可. 【解答】解:∵f()==2, ∴f(f())=f(2)=e2﹣1=e, 故答案为:e. 14.已知f(x)=x3﹣3x+8,则曲线y=f(x)在点(2,f(2))处的切线斜率为 9 . 【考点】利用导数研究曲线上某点切线方程. 【分析】求出函数的导数,令x=2即可得到切线的斜率. 【解答】解:f(x)=x3﹣3x+8的导数为f′(x)=3x2﹣3, 即有曲线y=f(x)在点(2,f(2))处的切线斜率为k=3×22﹣3=9, 故答案为:9. 15.在区间[0,9]上随机取一实数x,则该实数x满足不等式1≤log2x≤2的概率为 . 【考点】几何概型;指、对数不等式的解法. 【分析】解不等式1≤log2x≤2,可得2≤x≤4,以长度为测度,即可求在区间[0,9]上随机取一实数x,该实数x满足不等式1≤log2x≤2的概率. 【解答】解:本题属于几何概型 解不等式1≤log2x≤2,可得2≤x≤4, ∴在区间[0,9]上随机取一实数x,该实数x满足不等式1≤log2x≤2的概率为 故答案为: 16.过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若,则|AF|= . 【考点】抛物线的简单性质. 【分析】设出点的坐标与直线的方程,利用抛物线的定义表示出|AF|、|BF|再联立直线与抛物线的方程利用根与系数的关系解决问题,即可得到答案. 【解答】解:由题意可得:F(,0),设A(x1,y1),B(x2,y2). 因为过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点, 所以|AF|=+x1,|BF|=+x2. 因为,所以x1+x2= 设直线l的方程为y=k(x﹣), 联立直线与抛物线的方程可得:k2x2﹣(k2+2)x+=0, 所以x1+x2=. ∴ ∴k2=24 ∴24x2﹣26x+6=0, ∴, ∴|AF|=+x1= 故答案为: 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.设,若“a=1”是“A∩B≠Φ”的充分条件,则实数b的取值范围是 (﹣2,2) . 【考点】绝对值不等式;必要条件、充分条件与充要条件的判断;其他不等式的解法. 【分析】化简集合A、集合B,根据a=1时,A∩B≠Φ,可得b=0 满足条件,当b≠0时,应有 b﹣1<﹣1<b+1,或 b﹣1<1<b+1, 分别求出b的范围后,再取并集,即得所求. 【解答】解:∵={x|﹣1<x<1}, B={x||x﹣b|<a}={x|b﹣a<x<b+a}, ∵“a=1”是“A∩B≠Φ”的充分条件,∴{x|﹣1<x<1}∩{x|b﹣1<x<b+1}≠Φ, 当b=0时,A=B,满足条件. 当b≠0时,应有 b﹣1<﹣1<b+1,或 b﹣1<1<b+1. 解得﹣2<b<0,或 0<b<2. 综上可得﹣2<b<2, 故答案为 (﹣2,2). 18.已知双曲线C:﹣=1(a>0,b>0)的离心率为,实轴长为2. (1)求双曲线C的方程; (2)若直线y=x+m被双曲线C截得的弦长为,求m的值. 【考点】直线与圆锥曲线的综合问题. 【分析】(1)由离心率为,实轴长为2.可得,2a=2,再利用b2=c2﹣a2=2即可得出. (2)设A(x1,y1),B(x2,y2),与双曲线的联立可得x2﹣2mx﹣m2﹣2=0,利用根与系数的关系可得|AB|===4,即可得出. 【解答】解:(1)由离心率为,实轴长为2. ∴,2a=2,解得a=1,, ∴b2=c2﹣a2=2, ∴所求双曲线C的方程为=1. (2)设A(x1,y1),B(x2,y2), 联立, △>0,化为m2+1>0. ∴x1+x2=2m,. ∴|AB|===4, 化为m2=1, 解得m=±1. 19.某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组[1,3),第二组[3,5),第三组[5,7),第四组[7,9),第五组[9,11],绘制成如图所示的频率分布直方图. (Ⅰ)求学习时间在[7,9)的学生人数; (Ⅱ)现要从第三组、第四组中用分层抽样的方法抽取6人,从这6人中随机抽取2人交流学习心得,求这2人中至少有1人的学习时间在第四组的概率. 【考点】列举法计算基本事件数及事件发生的概率;频率分布直方图. 【分析】(Ⅰ)由频率分布图求出x=0.100,由此能求出学习时间在[7,9)的学生人数. (Ⅱ)第三组的学生人数为40人,利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为:第三组的人数为4人,第四组的人数为2人,由此能求出这2人中至少有1人的学习时间在第四组的概率. 【解答】解:(Ⅰ)由频率分布图得:0.025×2+0.125×2+0.200×2+2x+0.050×2=1, 解得x=0.100. ∴学习时间在[7,9)的学生人数为0.010×2×100=20人. (Ⅱ)第三组的学生人数为0.200×2×100=40人, 第三、四组共有20+40=60人, 利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为: 第三组的人数为6×=4人,第四组的人数为6×=2人, 则从这6人中抽2人,基本事件总数n==15, 其中2人学习时间都不在第四组的基本事件个数m==6, ∴这2人中至少有1人的学习时间在第四组的概率: p=1﹣=. 20.已知函数f(x)=x2+(x≠0,a∈R). (1)判断函数f(x)的奇偶性; (2)若f(x)在区间[2,+∞)上是增函数,求实数a的取值范围. 【考点】函数单调性的判断与证明;函数奇偶性的判断. 【分析】(1)根据偶函数、奇函数的定义,便容易看出a=0时,f(x)为偶函数,a≠0时,f(x)便非奇非偶; (2)根据题意便有f′(x)=在[2,+∞)上恒成立,这样便可得到a≤2x3恒成立,由于2x3为增函数,从而可以得出a≤16,这便可得到实数a的取值范围. 【解答】解:(1)①当a=0时,f(x)=x2为偶函数; ②当a≠0时,f(1)=1+a,f(﹣1)=1﹣a; 显然f(﹣1)≠f(1),且f(﹣1)≠﹣f(1),∴f(x)既不是奇函数,也不是偶函数; (2)f′(x)=2x,要使f(x)在[2,+∞)上是增函数; 只需当x≥2时,f′(x)≥0恒成立; 即恒成立; ∴a≤2x3; 又x≥2; ∴函数2x3的最小值为16; ∴a≤16; ∴实数a的取值范围为(﹣∞,16] 21.已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为F(﹣,0),且右顶点为D(2,0).设点A的坐标是(1,). (1)求该椭圆的标准方程; (2)过原点O的直线交椭圆于点B、C,求△ABC面积的最大值. 【考点】直线与圆锥曲线的关系;点到直线的距离公式;椭圆的标准方程. 【分析】(Ⅰ)由左焦点为,右顶点为D(2,0),得到椭圆的半长轴a,半焦距c,再求得半短轴b,最后由椭圆的焦点在x轴上求得方程. (2)当BC垂直于x轴时,BC=2,S△ABC=1;当BC不垂直于x轴时,设该直线方程为y=kx,代入椭圆方程,求得B,C的坐标,进而求得弦长|BC|,再求原点到直线的距离,从而可得三角形面积模型,再用基本不等式求其最值. 【解答】解:(Ⅰ)由已知得椭圆的半长轴a=2,半焦距c=,则半短轴b=1. 又椭圆的焦点在x轴上, ∴椭圆的标准方程为 (II)当BC垂直于x轴时,BC=2,S△ABC=1 当BC不垂直于x轴时,设该直线方程为y=kx,代入 解得B(),C(), 则,又点A到直线BC的距离d=, ∴△ABC的面积S△ABC= 于是S△ABC= 要使△ABC面积的最大值,则k<0 由≥﹣1,得S△ABC≤,其中,当k=时,等号成立. ∴S△ABC的最大值是 22.设函数,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0. (1)求y=f(x)的解析式; (2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值. 【考点】利用导数研究曲线上某点切线方程;导数的几何意义;直线的一般式方程. 【分析】(1)已知曲线上的点,并且知道过此点的切线方程,容易求出斜率,又知点(2,f(2))在曲线上,利用方程联立解出a,b (2)可以设P(x0,y0)为曲线上任一点,得到切线方程,再利用切线方程分别与直线x=0和直线y=x联立,得到交点坐标,接着利用三角形面积公式即可. 【解答】解析:(1)方程7x﹣4y﹣12=0可化为,当x=2时,, 又,于是,解得,故. (2)设P(x0,y0)为曲线上任一点,由知曲线在点P(x0,y0)处的切线方程为,即 令x=0,得,从而得切线与直线x=0的交点坐标为; 令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0); 所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为. 故曲线y=f(x)上任一点处的切线与直线x=0,y=x所围成的三角形面积为定值,此定值为6.查看更多