河北省新乐市第一中学2019-2020学年高二下学期6月月考数学试题

河北省新乐市第一中学2019-2020学年高二下学期6月月考数学试题

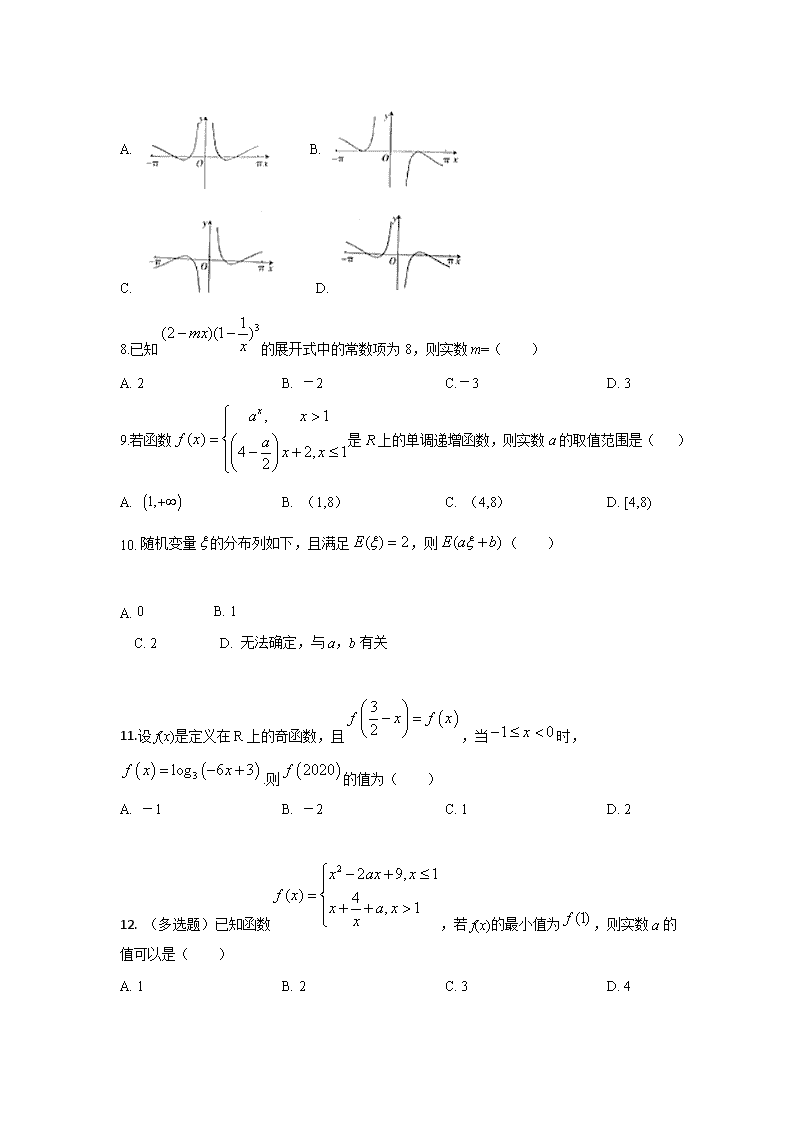
高二第二次月考数学试题 一．选择题（本题共 12 道小题，每小题 0 分，共 0 分） 1.在复平面内，复数 z 对应的点的坐标为(2,－1)，则 等于( ) A. B. C. D. 2.已知全集 U＝R，集合 A＝{x|x2－x－6≤0}，B＝{x| ＞0}，那么集合 A∩(∁UB)＝(　　) A. {x|－2≤x＜4} B. {x|x≤3 或 x≥4} C. {x|－2≤x＜－1} D. {x|－1≤x≤3} 3.（多选题）下列命题中是真命题的是（ ） A. “ ”是“ ”的充分不必要条件； B. 命题“ ，都有 ”的否定是“ ，使得 ”； C. 数据 ， ， ， 的平均数为 6，则数据 ， ， ， 的平均数 是 6； D. 若随机变量 服从正态分布 ， ，则 ． 4.已知 ， ， ，则 a、b、c 的大小关系为（ ） A. B. C. D. 5.某单位举行诗词大会比赛，给每位参赛者设计了“保留题型”､“升级题型”､“创新题型”三类 题型，每类题型均指定一道题让参赛者回答．已知某位参赛者答对每道题的概率均为 ， 且各次答对与否相互独立，则该参赛者答完三道题后至少答对两道题的概率（ ） A. B. C. D. 6.2019 义乌国际马拉松赛，某校要从甲乙丙丁等 10 人中挑选 3 人参加比赛，其中甲乙丙丁 4 人中至少有 1 人参加且甲乙不同时参加，丙丁也不同时参加，则不同的报名方案有（ ） A. 69 B. 96 C. 76 D. 84 7..函数 在 的图像大致为（ ） (1 i)z+ 3 i+ 2 i+ 1 i+ 1 i− 1 4 x x + − 1x > 2 1x > 0x∀ > sin 1x ≤ 0 0x∃ > 0sin 1x > 1x 2x ⋅⋅⋅ 8x 12 5x − 22 5x − ⋅⋅⋅ 82 5x − ξ ( )21,N σ ( )4 0.79P ξ ≤ = ( )2 0.21P ξ ≤ − = 3log 2a = 5log 6b = ln 2c = a c b< < c a b< < a b c< < c b a< < 4 5 112 125 80 125 113 125 124 125 ( ) ln cos sin x xf x x x ⋅= + [ ) ( ],0 0,π π− ∩ A. B. C. D. 8.已知 的展开式中的常数项为 8，则实数 m=（ ） A. 2 B. －2 C.－3 D. 3 9.若函数 是 R 上的单调递增函数，则实数 a 的取值范围是（ ） A. B. （1,8） C. （4,8） D. [4,8) 10. 随机变量 的分布列如下，且满足 ，则 （　　） A. 0 B. 1 C. 2 D. 无法确定，与 a，b 有关 11.设 f(x)是定义在 R 上的奇函数，且 ，当 时， .则 的值为（ ） A. －1 B. －2 C. 1 D. 2 12. （多选题）已知函数 ，若 f(x)的最小值为 ，则实数 a 的 值可以是（ ） A. 1 B. 2 C. 3 D. 4 1 2 3 P a b c 31(2 )(1 )mx x − − , 1 ( ) 4 2, 12 xa x f x a x x  > =  − + ≤   ( )1,+∞ ξ ( ) 2E ξ = ( )E a bξ + ( )3 2f x f x − =   1 0x− ≤ < ( ) ( )3log 6 3f x x= − + ( )2020f 2 2 9, 1 ( ) 4 , 1 x ax x f x x a xx  − + ≤=  + + > (1)f ξ 二、填空题. 13.设服从二项分布 的随机变量 的期望与方差分别是 15 和 ，则 n=____， p=____． 14. 的展开式中 项的系数是________. 15.函数 的单调递增区间是________. 16.已知函数 的值域是 R，则实数 a 的取值范围是 __________. 三．解答题 17.已知函数 为奇函数，且当 时， ． （1）求当 时，函数 f(x)的表达式； （2）解不等式 ． 18.已知函数 . （1）当 时，求函数 f(x)的值域； （2）若函数 f(x)在[－1,3]上的最大值为 1，求实数 a 的值. 19.新高考，取消文理科，实行“3+3”，成绩由语文、数学、外语统一高考成绩和自主选考的 3 门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况， 随机调查 50 人（把年龄在[15,45)称为中青年，年龄在[45,75)称为中老年），并把调查结果制 成下表： 年龄（岁） [15,25) [25,35) [35,45) [45,55) [55,65) [65,75) 频数 5 15 10 10 5 5 了解 4 12 6 5 2 1 ( ),B n p ξ 45 4 8 21 2 yx + −   2 2x y )32(log)( 2 3 1 ++−= xxxf { 1,3)21( 1,ln)( <+− ≥= xaxa xxxf ( )f x 0x > ( ) 1 3 log 2f x x= 0x < ( ) 3f x ≤ 2( ) (2 1) 3f x x a x= + − − [2 2 ]3a x= −∈， ， （1）分别估计中青年和中老年对新高考了解的概率； （2）请根据上表完成下面 2×2 列联表，是否有 95%的把握判断对新高考的了解与年龄（中 青年、中老年）有关？ 了解新高考 不了解新高考 总计 中青年 中老年 总计 附： . （3）若从年龄在[55,65)的被调查者中随机选取 3 人进行调查，记选中的 3 人中了解新高考 的人数为 X，求 X 的分布列以及 . 20.某超市在节日期间进行有奖促销，凡在该超市购物满 400 元的顾客，将获得一次摸奖机 会，规则如下：奖盒中放有除颜色外完全相同的 1 个红球，1 个黄球，1 个白球和 1 个黑球 顾客不放回的每次摸出 1 个球，若摸到黑球则停止摸奖，否则就继续摸球规定摸到红球奖励 20 元，摸到白球或黄球奖励 10 元，摸到黑球不奖励 （1）求 1 名顾客摸球 2 次停止摸奖的概率： （2）记 X 为 1 名顾客 5 次摸奖获得的奖金数额，求随机变量 X 的分布列和数学期望 21.甲、乙两人同时参加一个外贸公司的招聘,招聘分笔试与面试两部分,先笔试后面试.甲笔试 与面试通过的概率分别为 0.8,0.5,乙笔试与面试通过的概率分别为 0.8,0.4,且笔试通过了才能 进入面试,面试通过则直接招聘录用,两人笔试与面试相互独立互不影响. (1)求这两人至少有一人通过笔试的概率; (2)求这两人笔试都通过却都未被录用的概率; (3)记这两人中最终被录用的人数为 X,求 X 的分布列和数学期望. 22.已知二项式 的展开式中第五项为常数项. （1）求展开式中二项式系数最大的项； 0.050 0.010 0.001 3.841 6.635 10.828 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d −= + + + + ( )E X 2 2 +   n x x ( )2P K k≥ k （2）求展开式中有理项的系数和. 23.在 2016 年 8 月巴西里约热内卢举办的第 31 届奥运会上，乒乓球比赛团体决赛实行五场 三胜制，且任何一方获胜三场比赛即结束.甲、乙两个代表队最终进入决赛，根据双方排定 的出场顺序及以往战绩统计分析，甲队依次派出的五位选手分别战胜对手的概率如下表： 出场顺序 1 号 2 号 3 号 4 号 5 号 获胜概率 p q 若甲队横扫对手获胜（即 3∶0 获胜）的概率是 ，比赛至少打满 4 场的概率为 . （1）求 p，q 的值； （2）求甲队获胜场数的分布列和数学期望. 1 2 1 2 2 5 1 8 3 4 高二第二次月考数学试卷答案 1.A 2.D 3.A 4.C 5.B 6.D 7.A 8.C 9.B 10.B 11. ABD 12.BCD 13.60 14. 420 15. 16. 17. ， （ ）当 时， ， 或 ， 故 ． ． （ ）∵ ，∴ ， 当 时， ，∴ ， 当 时，即 时， 且 ， ∴ ，∴ ． 综上所述， ． 18.（1）当 时， ， 又 ，所以 ， ，所以值域为 . （2）对称轴为 . ①当 ，即 时， 所以 ，即 满足题意； ②当 ，即 时， 4 1 ），或（ 31)3,1[ )2 1,1[− { }| 3 4A x x= − ≤ ≤ 1 3m = { }| 2 7B x x= ≤ ≤ ( ) { | 2U B x x= < 7}x > [2,4]A B = ( ) ( ,4] (7, )UA B = −∞ +∞  2 A B B= B A⊆ B = ∅ 1 3 2m m− > − 1 2m < B ≠ ∅ 1 2m≥ 1 9m − −≥ 3 2 4m − ≤ 2 2m− ≤ ≤ 1 22 m≤ ≤ 2m≤ 2a = 2 2 3 21( ) 3 3 2 4f x x x x = + − = + −   2[ ]3x ∈ - ， 3 21( )min 2 4f x f  = − = −   max 3 15f x f= =（ ） （ ） 21,154 −     2 1 2 ax −= − 2 1 12 a −− ≤ 1 2a ≥ − max 3 6 3f x f a= = +（ ） （ ） ， 6 3 1a + = 1 3a = − 2 1 12 a −− > 1 2a < − ，所以 ，即 满足题意 综上可知 或 . 19.（1）∵前三项系数 、 、 成等差数列． ，即 ．∴ 或 (舍去） ∴展开式中通项公式 令 ，得 ， ∴含 x2 项的系数为 ； （2）当 为整数时， ． ∴展开式共有 9 项，共有 种排法． 其中有理项有 3 项，有理项互不相邻有 种排法， ∴有理项互不相邻的概率为 20.（1）由题中数据可知，中青年对新高考了解的概率 ， 中老年对新高考了解的概率 . （2） 列联表如图所示 了解新高考 不了解新高考 总计 中青年 22 8 30 老年 8 12 20 总计 30 20 50 ， 所以有 95%的把握判断了解新高考与年龄（中青年、中老年）有关联. （3）年龄在 的被调查者共 5 人，其中了解新高考的有 2 人， max 1 2 1f x f a= =（ ） （﹣） ﹣ ﹣， 2 1 1a =﹣ ﹣ 1a =﹣ 1 3a = − 1− 1 11 2 nC 21 4 nC 1 21 12 C 1 C2 4n n ∴ ⋅ = + 2 9 8 0n n− + = 8n = 1n = ( ) 28 4 3 1 8 6 1 1 22 r rr rr r r nT C x C x x − − +    = =       24 23 r− = 3r = 3 3 8 1 72C   =   24 3 r− 0,3,6r = 9 9A 6 3 6 7A A 6 3 6 7 9 9 5 12 A AP A = = 22 11 30 15P = = 8 2 20 5P = = 2 2× 2 2 50 (22 12 8 8) 5.56 3.84130 20 20 30K × × − ×= ≈ >× × × [55,65) 则抽取的 3 人中了解新高考的人数 可能取值为 0，1，2， 则 ； ； . 所以 的分布列为 0 1 2 . 21.（1）由题意 ， 解得 ． （2）设甲队获胜场数为 ，则 的可取的值为 0，1，2，3 ， ， ， ， 的分布列为 ． 0 1 2 3 X 0 3 2 3 3 5 1( 0) 10 C CP X C = = = 1 2 2 3 3 5 6 3( 1) 10 5 C CP X C = = = = 5 12 2 3 3 3( 2) 10 C CP X C = = = X X P 1 10 3 5 3 10 1 3 3 6( ) 0 1 210 5 10 5E X = × + × + × = 1 1 2 8 1 1 31 (1 )(1 )(1 )8 2 4 pq p q  =  − − − − − = 1 2p q= = ξ ξ 31 1( 0) ( )2 8P ξ = = = 1 2 3 1 1 1 3( 1) ( )2 2 2 16P Cξ = = ⋅ =⋅ ⋅ 2 2 2 4 1 1 3 9( 2) ( ) ( )2 2 5 40P Cξ = = =⋅ ⋅ ⋅ 3 2 2 2 2 2 3 4 1 1 1 1 1 1 2 37( 3) ( ) ( ) ( ) ( )2 2 2 2 2 2 5 80P C Cξ ⋅ ⋅ ⋅ ⋅ ⋅= = + ⋅ + = ξ∴ 1 3 9 37 810 1 2 38 16 40 80 40Eξ = × + × + × + × = ξ P 1 8 3 16 9 40 37 80 22.（1）因为定义域为 R 的函数 f（x）是奇函数， 所以 （2）因为定义域为 R 的函数 f（x）是奇函数 当 时， 又因为函数 f（x）是奇函数 综上所述 （3） 且 f（x）在 R 上单调，∴f（x）在 R 上单调递减 由 得 ∵f（x）是奇函数 又因为 f（x）是减函数 即 对任意 恒成立 得 即为所求．