专题8-1+空间几何体的结构及其三视图和直观图（测）-2018年高考数学（文）一轮复习讲练测

专题8-1+空间几何体的结构及其三视图和直观图（测）-2018年高考数学（文）一轮复习讲练测

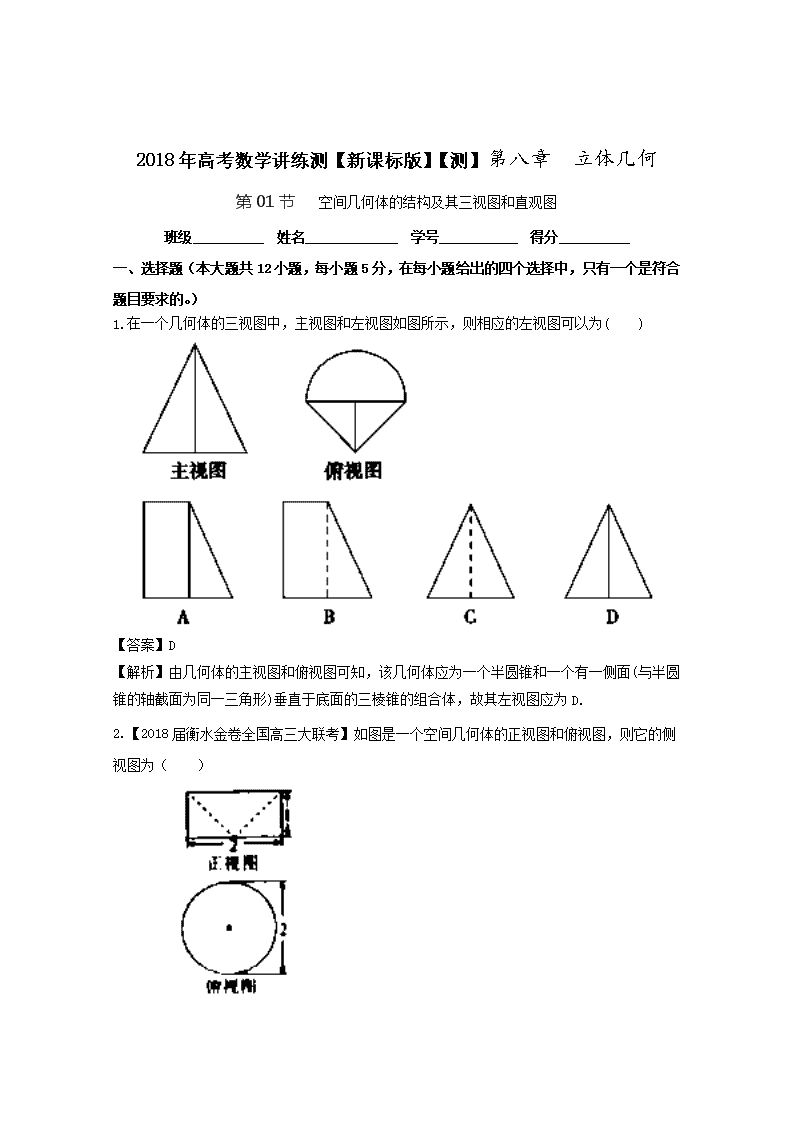
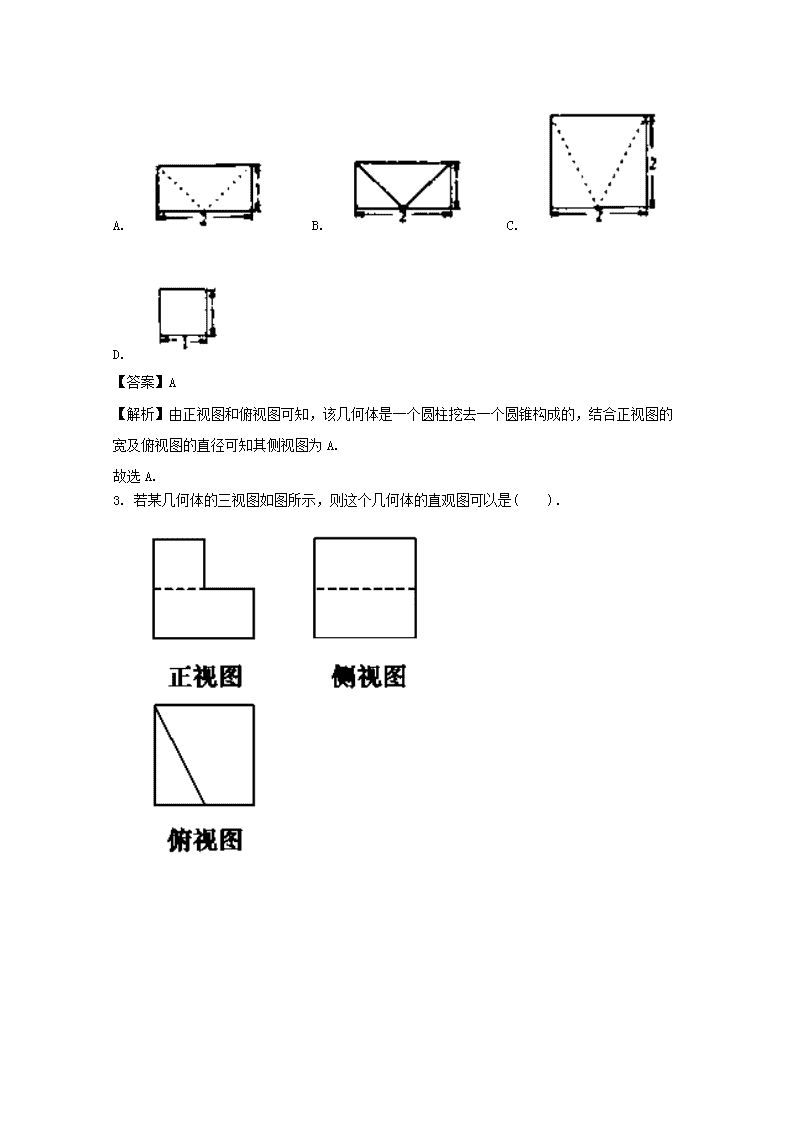
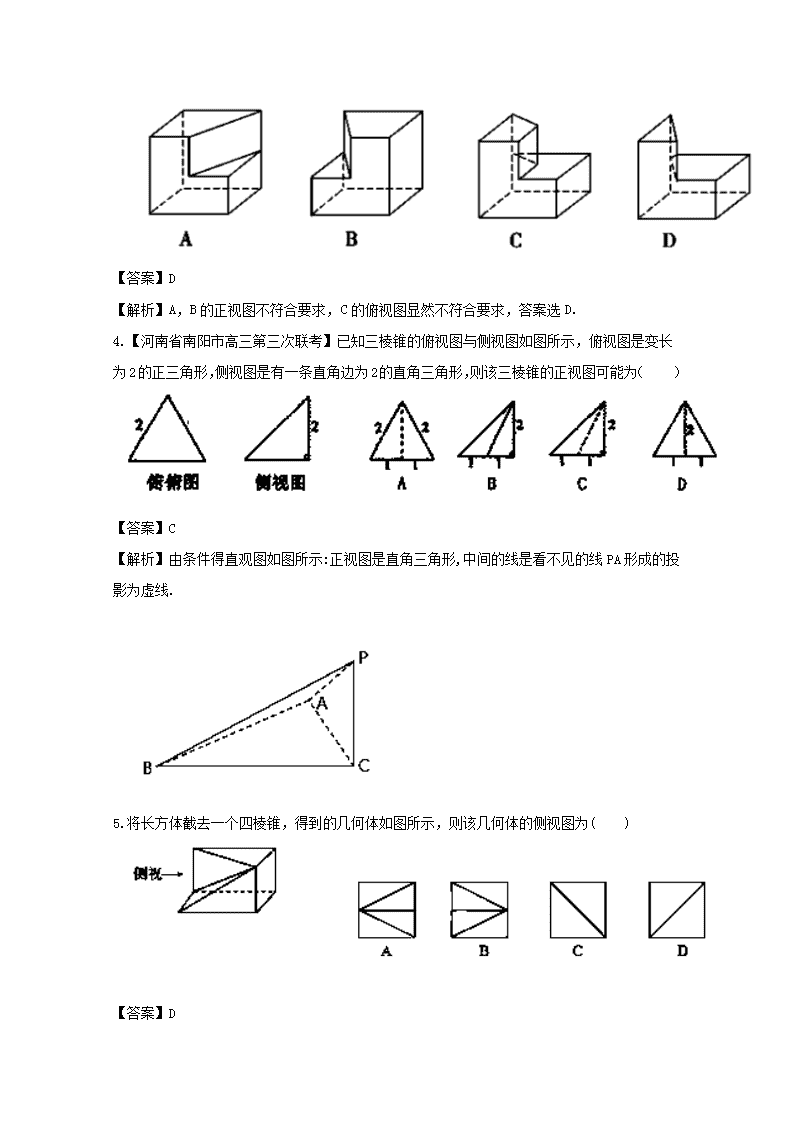
‎2018年高考数学讲练测【新课标版】【测】第八章 立体几何 第01节 空间几何体的结构及其三视图和直观图 班级__________ 姓名_____________ 学号___________ 得分__________‎ 一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的。）‎ ‎1.在一个几何体的三视图中，主视图和左视图如图所示，则相应的左视图可以为(　　)‎ ‎【答案】D ‎【解析】由几何体的主视图和俯视图可知，该几何体应为一个半圆锥和一个有一侧面(与半圆锥的轴截面为同一三角形)垂直于底面的三棱锥的组合体，故其左视图应为D.‎ ‎2.【2018届衡水金卷全国高三大联考】如图是一个空间几何体的正视图和俯视图，则它的侧视图为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】由正视图和俯视图可知，该几何体是一个圆柱挖去一个圆锥构成的，结合正视图的宽及俯视图的直径可知其侧视图为A.‎ 故选A.‎ ‎3. 若某几何体的三视图如图所示，则这个几何体的直观图可以是(　　)．‎ ‎【答案】D ‎【解析】A，B的正视图不符合要求，C的俯视图显然不符合要求，答案选D.‎ ‎4.【河南省南阳市高三第三次联考】已知三棱锥的俯视图与侧视图如图所示，俯视图是变长为2的正三角形，侧视图是有一条直角边为2的直角三角形，则该三棱锥的正视图可能为（ ）‎ ‎【答案】C ‎【解析】由条件得直观图如图所示:正视图是直角三角形,中间的线是看不见的线PA形成的投影为虚线.‎ ‎5.将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为(　　)‎ ‎ ‎ ‎【答案】D ‎【解析】左视图从图形的左边向右边看，看到一个正方形的面，在面上有一条对角线，对角线是由左下角都右上角的线，故选D．‎ ‎6.【2018届四川省成都市龙泉第二中学高三10月月考】一个几何体的三视图如图所示，则该几何体的表面积为( ) ‎ ‎ ‎ A. B. C. D. ‎ ‎【答案】D ‎7.【安徽蚌埠市期末】点B是点A（1，2，3）在坐标平面内的射影，则OB等于（ ）‎ A. B. C. D.‎ ‎【答案】A ‎【解析】根据题意可得，所以。故A正确.‎ ‎8.【四川卷】一个几何体的三视图如图所示，则该几何体的直观图可以是(　　)‎ 图1－3‎ ‎【答案】D ‎【解析】根据三视图原理，该几何体上部为圆台，下部为圆柱．‎ ‎9. 【新课标全国卷Ⅱ】一个四面体的顶点在空间直角坐标系O－xyz中的坐标分别是(1，0，1)，(1，1，0)，(0，1，1)，(0，0，0)，画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为(　　)‎ ‎【答案】A　‎ ‎【解析】在空间直角坐标系O－xyz中画出三棱锥，由已知可知三棱锥O－ABC为题中所描叙的四面体，而其在zOx平面上的投影为正方形EBDO，故选A.‎ ‎10. 【江西卷】一几何体的直观图如图，下列给出的四个俯视图中正确的是 ‎(　　)‎ ‎【答案】B ‎【解析】　由直观图可知，该几何体由一个长方体和一个截角三棱柱组成．从上往下看，外层轮廓线是一个矩形，矩形内部有一条线段连接的两个三角形．‎ ‎11. 小蚂蚁的家住在长方体的处，小蚂蚁的奶奶家住在处，三条棱长分别是， ， ，小蚂蚁从点出发，沿长方体的表面到小蚂蚁奶奶家的最短距离是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎12.【2017届江西省赣州市高三二模】正方体的棱长为1，点分别是棱的中点，过作一平面，使得平面平面，则平面截正方体的表面所得平面图形为（ ）‎ A. 三角形 B. 四边形 C. 五边形 D. 六边形 ‎【答案】D ‎【解析】由题意，在正方体中， 分别为棱的中点，‎ 取的中点，‎ 可得正六边形，此时平面平面，故选D.‎ 二、填空题（本大题共4小题，每小题5分，共20分。把答案填在题中的横线上。）‎ ‎13.如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，其中O′A′＝6‎ ‎ cm，O′C′＝2 cm，则原图形是 形.‎ ‎ ‎ ‎【答案】菱形 ‎14. 如图所示，E，F分别为正方体ABCD－A1B1C1D1的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的正投影可能是________(填序号)．‎ ‎【答案】②③‎ ‎【解析】　由正投影的定义，四边形BFD1E在面AA1D1D与面BB1C1C上的正投影是图③；其在面ABB1A1与面DCC1D1上的正投影是图②；其在面ABCD与面A1B1C1D1上的正投影也是②，故①④错误．‎ ‎15.【2018届河南省中原名校高三上第一次联考】某三棱锥的三视图如右图所示，则该三棱锥最长的棱为_________．‎ ‎【答案】3‎ ‎【解析】由三视图得到该几何体如图，‎ CD=1，BC=， BE=，CE=2，DE=3；‎ 所以最大值为3，故最长边为DE=3；‎ 故答案为：3．‎ ‎16.【2018届河南省郑州市第一中学高三上学期入学】已知三点都在体积为的球的表面上，若， ，则球心到平面的距离为__________．‎ ‎【答案】3‎ ‎【解析】设球的半径为， 平面，垂足为，因为球的体积为，所以，解得；因为，所以，又因为，所以，则球心到平面的距离为.‎ 三、解答题 （本大题共4小题，共50分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.【2017届重庆市第一中学高三数学一轮】画出三视图.‎ ‎【答案】见解析 试题解析:原几何体的三视图如下：‎ ‎18.【2017届重庆市第一中学高三数学一轮复习】已知：图①是截去一个角的长方体，试按图示的方向画出其三视图；图②是某几何体的三视图，试说明该几何体的构成．‎ ‎【答案】见解析 ‎【解析】试题分析: ①在画三视图时，能看见的轮廓线和棱用实线表示，重叠的线只画一条，不能看见的轮廓线和棱用虚线表示．三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体的正投影图．②根据三视图的形成原理，结合具体柱、锥的三视图,空间想象将三视图还原为实物图．‎ 试题解析:图①几何体的三视图为：‎ 图②所示的几何体是上面为正六棱柱，‎ 下面为倒立的正六棱锥的组合体．‎ ‎19.【2018届湖北省宜昌市葛洲坝中学高三9月月考】在如图所示的正方体ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎中，‎ ‎（1）过点C作与面A‎1‎BD平行的截面；‎ ‎（2）求证：‎AC‎1‎⊥面A‎1‎BD ‎（3）若正方体的棱长为2，求四面体A‎1‎BC‎1‎D的体积。‎ ‎【答案】（1）见解析；（2）见解析；（3）.‎ 试题解析：‎ ‎(1)见下图 ‎ ‎ ‎(2)证明： 正方体ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎， CC‎1‎⊥面ABCD ‎‎∴CC‎1‎⊥BD 又有 AC⊥BD‎,‎∴BD⊥面ACC‎1‎A‎1‎,‎‎∵AC‎1‎⊂面ACC‎1‎A‎1‎，∴BD⊥AC‎1‎ 同理AC‎1‎⊥A‎1‎B,而BD∩A‎1‎B=B,‎∴AC‎1‎⊥面A‎1‎BD。‎ ‎(3)法一（直接计算）由（2）知AC‎1‎⊥面A‎1‎BD，设垂足为O,由等积法知AO=‎2‎‎3‎‎3‎,∴C‎1‎O=‎‎4‎‎3‎‎3‎ ‎∴VA‎1‎BC‎1‎D=‎1‎‎3‎SΔA‎1‎BD·C‎1‎O=‎1‎‎3‎⋅‎3‎‎4‎⋅‎2‎‎2‎‎2‎⋅‎4‎‎3‎‎3‎=‎‎8‎‎3‎‎ ‎ 法二：（间接计算）用正方体体积减去四个角落的体积 ‎20. 在长方体ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎中，E,F分别是AD,DD‎1‎的中点，AB=BC=2‎，过A‎1‎‎、C‎1‎、B三点的的平面截去长方体的一个角后．得到如图所示的几何体ABCD-‎A‎1‎C‎1‎D‎1‎，且这个几何体的体积为‎40‎‎3‎．‎ ‎（1）求证：EF//‎平面A‎1‎BC‎1‎；‎ ‎（2）求A‎1‎A的长；‎ ‎（3）在线段BC‎1‎上是否存在点P，使直线A‎1‎P与C‎1‎D垂直，如果存在，求线段A‎1‎P的长，如果不存在，请说明理由．‎ ‎【答案】(1)证明见解析；(2)；(3).‎ 试题解析：解：（1）在长方体ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎中，可知AB//D‎1‎C‎1‎,AB=‎D‎1‎C‎1‎，由四边形ABC‎1‎D‎1‎是平行四边形，所以AD‎1‎‎//‎‎_‎‎_‎BC‎1‎.因为E,F分别是AD,DD‎1‎的中点，所以AD‎1‎//EF，则EF//BC‎1‎，‎ 又EF⊄‎面A‎1‎BC‎1‎,BC‎1‎⊂‎面A‎1‎BC‎1‎，则EF//‎平面A‎1‎BC‎1‎.‎ ‎（2）∵VABCD-‎A‎1‎C‎1‎D‎1‎‎=VABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎-VB-‎A‎1‎B‎1‎C‎1‎=2×2×AA‎1‎-‎1‎‎3‎×‎1‎‎2‎×2×2×AA‎1‎=‎10‎‎3‎AA‎1‎=‎‎40‎‎3‎，‎ ‎∴AA‎1‎=4‎.‎ ‎（3）在平面CC‎1‎D‎1‎D中作D‎1‎Q⊥C‎1‎D交CC‎1‎于，过作QP//CB交BC‎1‎于点P，则A‎1‎P⊥C‎1‎D.‎ 因为A‎1‎D‎1‎‎⊥‎平面CC‎1‎D‎1‎D,C‎1‎D⊂‎平面CC‎1‎D‎1‎D，∴C‎1‎D⊥‎A‎1‎D‎1‎，而 QP//CB,CB//‎A‎1‎D‎1‎‎，∴QP//‎A‎1‎D‎1‎，‎ 又∵A‎1‎D‎1‎‎∩D‎1‎Q=‎D‎1‎，∴C‎1‎D⊥‎平面A‎1‎PQC‎1‎,‎ 且A‎1‎P⊂‎平面A‎1‎PQC‎1‎，∴A‎1‎P⊥C‎1‎D，‎ ‎∵ΔD‎1‎C‎1‎Q∼RtΔC‎1‎CD，∴C‎1‎QCD‎=‎D‎1‎C‎1‎C‎1‎C，∴C‎1‎Q=1‎，又∵PQ//BC，∴PQ=‎1‎‎4‎BC=‎‎1‎‎2‎．‎ ‎∵四边形A‎1‎PQD‎1‎为直角梯形，且高D‎1‎Q=‎‎5‎，∴A‎1‎P=‎(2-‎1‎‎2‎)‎‎2‎‎+5‎=‎‎29‎‎2‎． ‎ ‎ ‎