小学数学小升初空间与图形专项训练试题

小学数学小升初空间与图形专项训练试题

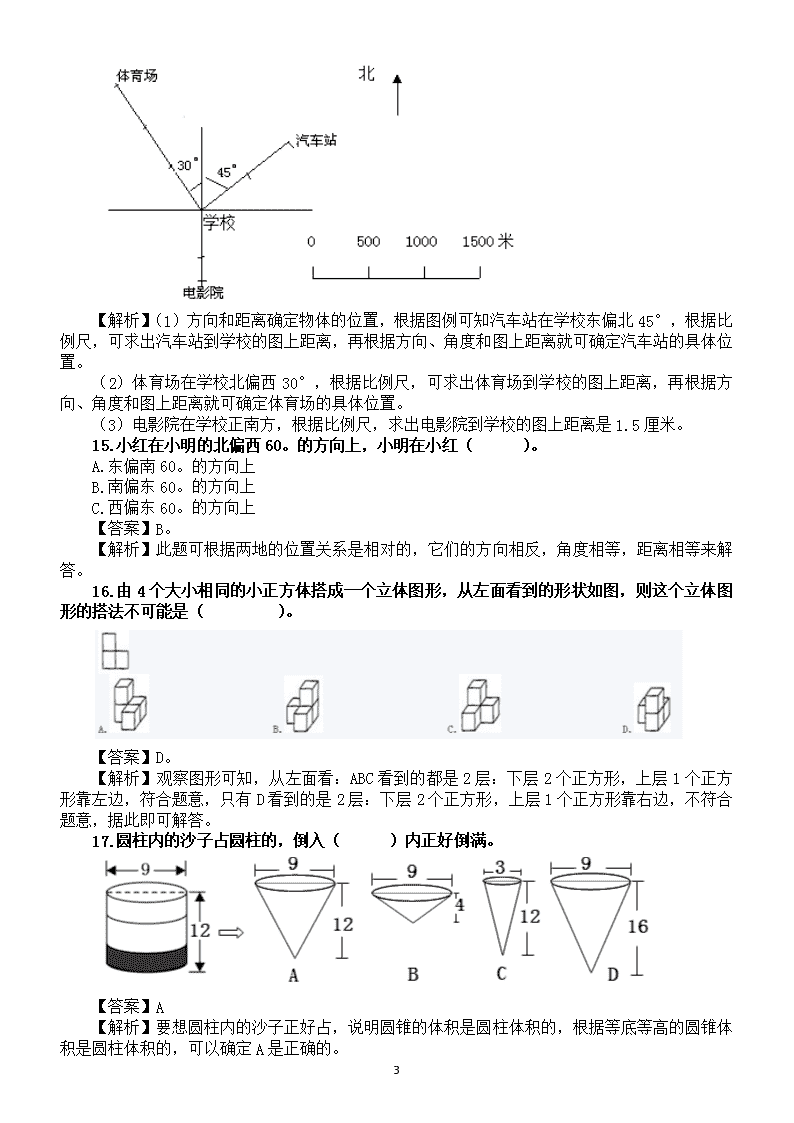
小升初数学空间与图形专项训练试题 基础题 一、选择题 ‎1.一个长方体的长、宽、高都扩大2倍，它的体积扩大（ ）倍。‎ A、2    B、6    C、8‎ ‎【答案】C ‎【解析】长方体的体积=长×宽×高，长、宽和高都扩大2倍，则体积就扩大了2×2×2=8倍，根据此选择即可。‎ ‎2.正方体的棱长扩大2倍，它的表面积就（       ）。‎ A.扩大2倍       B.扩大4倍       C.扩大6倍 ‎【答案】B ‎【解析】根据正方体的表面积计算公式，棱长扩大2倍，则表面积扩大：2×2=4倍，根据此选择即可。‎ ‎3.用两个棱长是1分米的正方体小木块拼成一个长方体，拼成的长方体的表面积是（    ）。‎ A.增加了        B.减少了         C.没有变 ‎【答案】B ‎【解析】把小正方体拼成一个长方体后，减少了2个小正方形的面积，因此拼成的长方体的表面积比原来减少了。‎ ‎4.做一个长方体抽屉，需要（     ）块长方形木板。‎ A.4           B.5          C.6‎ ‎【答案】B ‎【解析】长方体抽屉没有上面一个面，因此一共有5个面，需要5块长方形木板，根据此选择即可。‎ ‎5.用一根长（       ）铁丝正好可以做一个长6厘米、宽5厘米、高3厘米的长方体框架。‎ A.28厘米         B.126平方厘米        C.56厘米         D.90立方厘米 ‎【答案】C。‎ ‎【解析】长方体有4条长，4条宽和4条高，求出棱长之和，即可求出需要多少铁丝，即：（6＋5＋3）×4=56厘米，根据此选择即可。‎ ‎6.我们在画长方体时一般只画出三个面，这是因为长方体（        ）。‎ A.只有三个面      B.只能看到三个面     C.最多只能看到三个面 ‎【答案】C ‎【解析】把长方体放在桌面上，最多可以看到3个面。根据此选择。‎ ‎7.将一个正方体钢坯锻造成长方体，正方体和长方体（         ）。‎ A.体积相等，表面积不相等 B.体积和表面积都不相等.‎ C.表面积相等，体积不相等.‎ ‎【答案】A ‎【解析】将一个正方体钢坯锻造成长方体，形状改变，体积不变。‎ ‎8.一个正方体的棱长之和是12a厘米，它的棱长是（    ）厘米。‎ A.6a     B.a      C.2a     D.12a ‎【答案】B ‎【解析】棱长之和÷12=棱长 19‎ ‎9.一个正方体的棱长是8分米，它的棱长总和是（    ）分米。‎ A.48     B.64     C.32     D.96‎ ‎【答案】D ‎【解析】正方体的棱长之和=棱长×12‎ ‎10.一个圆锥的体积是12立方厘米，底面积是4平方厘米，高是（      ）厘米。‎ A、3         B、6      C、9        D、12‎ ‎【答案】C。‎ ‎【解析】圆锥的体积=×底面积×高，则高=3×圆锥的体积÷底面积，所以高为：3×12÷4=9厘米，根据此选择即可。‎ ‎11.沿着圆柱上下两个底面的直径把圆柱切开，可以得出（   ）形。‎ A.长方形     B.圆形    C.梯形 ‎【答案】A。‎ ‎【解析】沿着圆柱的上下两个底面的直径把圆柱切开，可以得出长方形。根据此选择即可。‎ ‎12.一个圆锥是由橡皮泥捏成的，要切一刀把它分成两块，（   ）切割，截面会是圆；（    ）切割，截面会是三角形。‎ A.垂直于底面            B.平行于底面 ‎【答案】B；A。‎ ‎【解析】一个圆锥是由橡皮泥捏成的，要切一刀把它分成两块，平行于底面切割，截面会是圆；垂直于底面切割，截面会是三角形，根据此选择即可。‎ ‎13.沿着圆柱的高，把圆柱的侧面展开，得不到（）。‎ A. 梯形  B.长方形   C.正方形 ‎【答案】A ‎【解析】沿着圆柱的高把圆柱的侧面展开，可以得到长方形或正方形，根据此选择即可。‎ ‎14.以学校为观测点，根据下列条件在图上标出各场所的位置。‎ ‎(1)汽车站在学校北偏东45°方向1000米处。‎ ‎(2)体育场在学校北偏西30°方向1500米处。‎ ‎(3)电影院在学校正南方750米处。‎ ‎【答案】（1）汽车站到学校的图上距离是：1000÷500=2（厘米）‎ ‎（2）体育场到学校的图上距离：1500÷500=3（厘米）‎ ‎（3）750÷500=1.5（厘米）‎ 根据各自的方向及图上距离，画图如下：‎ 19‎ ‎【解析】（1）方向和距离确定物体的位置，根据图例可知汽车站在学校东偏北45°，根据比例尺，可求出汽车站到学校的图上距离，再根据方向、角度和图上距离就可确定汽车站的具体位置。‎ ‎（2）体育场在学校北偏西30°，根据比例尺，可求出体育场到学校的图上距离，再根据方向、角度和图上距离就可确定体育场的具体位置。‎ ‎（3）电影院在学校正南方，根据比例尺，求出电影院到学校的图上距离是1.5厘米。‎ ‎15.小红在小明的北偏西60。的方向上，小明在小红（    ）。‎ A.东偏南60。的方向上 B.南偏东60。的方向上 C.西偏东60。的方向上 ‎【答案】B。‎ ‎【解析】此题可根据两地的位置关系是相对的，它们的方向相反，角度相等，距离相等来解答。‎ ‎16.由4个大小相同的小正方体搭成一个立体图形，从左面看到的形状如图，则这个立体图形的搭法不可能是（      ）。‎ ‎【答案】D。‎ ‎【解析】观察图形可知，从左面看：ABC看到的都是2层：下层2个正方形，上层1个正方形靠左边，符合题意，只有D看到的是2层：下层2个正方形，上层1个正方形靠右边，不符合题意，据此即可解答。‎ ‎17.圆柱内的沙子占圆柱的，倒入（    ）内正好倒满。‎ ‎【答案】A ‎【解析】要想圆柱内的沙子正好占，说明圆锥的体积是圆柱体积的，根据等底等高的圆锥体积是圆柱体积的，可以确定A是正确的。‎ 19‎ ‎18.边长4分米的正方形周长和面积相比（     ）。‎ A.周长大         B.面积大         C.一样大        D.无法比较 ‎【答案】D。‎ ‎【解析】周长和面积的意义不同、计算方法不同、计量单位不同，所以不能比较大小。‎ ‎19.乘坐电梯属于（  ）‎ A.平移B.旋转C.平行 ‎【答案】A.‎ ‎【解析】电梯上升是电梯整体向上移动，电梯的各对应点都向上作相同距离的移动，根据平移的意义，平移是指在同一平面内，将一个图形上的所有点都按照某个方向作相同距离的移动.据此判断电梯上的现象属于平移现象.‎ 解：电梯的上升，电梯的各对应点都向上作相同距离的移动，属于平移现象；‎ ‎20.体积单位和面积单位相比较，（  ）.‎ ‎①体积单位大  ②面积单位大      ③一样大  ④不能相比 ‎【答案】④‎ ‎【解析】体积单位和面积单位是不同的计量单位，所以无法比较。‎ ‎21.底面周长相等的两个圆柱，它们的（   ）一定相等。‎ A、表面积        B、侧面积         C、底面积 ‎【答案】C ‎【解析】根据的圆柱的特征，圆柱的上下两个底面是完全相同的两个圆，如果两个圆柱的底面周长相等，那么这两个圆的底面半径也相等，由此可以推出底面面积也一定相等。而在计算表面积和侧面积时都需要用到圆柱的高，题目中两个圆柱的高没有给出，所以不能确定。‎ ‎22.圆柱的侧面展开不可能是（   ）‎ A、长方形  B、正方形   C、平行四边形   D、梯形 ‎【答案】D ‎【解析】圆柱的侧面沿高剪开可能是长方形或正方形，如果斜着剪开可能会得到平行四边形，但因为上下两个圆大小相等，所以不可能得到上下两底大小不同的梯形。‎ ‎23.下面的物体（      ）是圆柱。‎ A、易拉罐     B、粉笔    C、魔方    D、课本 ‎【答案】A ‎【解析】课本是长方体，魔方是正方体，粉笔的上下两个底面大小不相等，易拉罐的上下两个底面相等，也符合圆柱的特征。‎ ‎24.两个长方形的周长相等，它们的面积（     ）。‎ A.相等 B.不相等 C.不一定相等 ‎【答案】C ‎【解析】两个长方形的周长相等，它们的面积不一定相等。‎ ‎25.一个正方体的棱长和是36厘米，它的表面积是 （   ）平方厘米。‎ A.36    B.27    C.54       D.48‎ ‎【答案】C ‎【解析】棱长总和除以12，得出一条棱的长度，然后根据正方体的表面积＝棱长×棱长×6：36÷12＝3（厘米）‎ ‎3×3×6＝54（平方厘米）；据此选择即可。‎ 二、填空题 ‎26.把三个棱长是1厘米的正方体拼成一个长方体，这个长方体的表面积是（      ），比原来3个正方体表面积之和减少了（      ）。‎ ‎【答案】故答案为：14平方厘米；4平方厘米 19‎ ‎【解析】把3个棱长是1厘米的正方体拼成一个长方体，长方体的长是3×1=3厘米，宽和高都是1厘米，根据长方体的表面积计算公式，把数据代入公式即可求出长方体的表面积，即：（3×1＋3×1＋1×1）×2=14平方厘米，3小正方体的表面积为1×1×6×3=18平方厘米，减少了18－14=4平方厘米，根据此填空。‎ ‎27.把三个棱长是2分米的正方体拼成一个长方体，表面积是（      ）。‎ ‎【答案】故答案为：56平方分米 ‎【解析】把3个棱长是2分米的正方体拼成一个长方体，长方体的长是3×2=6分米，宽和高都是2分米，根据长方体的表面积计算公式，把数据代入即可求出结果。‎ ‎28.正方体的棱长扩大3倍，它的表面积就扩大（     ）倍。‎ ‎【答案】故答案为：9‎ ‎【解析】根据正方体的表面积计算公式=棱长×棱长×6，棱长扩大3倍，则表面积扩大3×3=9倍，根据此填空即可。‎ ‎29.一个正方体的棱长总和是72厘米，它的一个面是边长（        ）厘米的正方形，它的表面积是（         ）平方厘米。‎ ‎【答案】故答案为：6；216‎ ‎【解析】正方体的12条棱相等，72÷12=6厘米，根据正方形的表面积=棱长×棱长×6，把数据代入公式即可，根据此填空。‎ ‎30.一个棱长是3m的正方体，它的棱长总和是（      ）m，其中一个面的面积是（     ）㎡。‎ ‎【答案】故答案为：36；9‎ ‎【解析】正方体有12条棱，每条棱的长度一样，用每条棱的长度×12就可求出棱长之和是多少，正方体的六个面都是正方形，因此根据正方形的面积计算公式，即可求出结果。根据此填空。‎ ‎31.长方体有（     ）个面，每个面都是（       ）形状，也可能有（    ）个相对的面是（       ）形。‎ ‎【答案】故答案为：6；长方形；2；正方形 ‎【解析】长方体有6个面，每个面都是长方形，但在长方体中最多有两个面是正方形，根据此填空即可。‎ ‎32.一个正方体的棱长是1cm，表面积是（      ），体积是（      ）。‎ ‎【答案】 6平方厘米，1立方厘米 ‎【解析】表面积就是6个面的总面积，棱长1厘米的正方体体积是1立方厘米。‎ ‎33.长方体和正方体的相同点是都有（   ）个面，（    ）条棱，（    ）个顶点。‎ ‎【答案】6    12    8‎ ‎【解析】根据长方体和正方体的区别与联系填空。‎ ‎34.以学校为观测点：‎ ‎①邮局在学校北偏的方向上，距离是_______米。‎ 19‎ ‎②书店在学校偏的方向上，距离是_______米。‎ ‎③图书馆在学校偏的方向上，距离是_____米。‎ ‎④电影院在学校偏的方向上，距离是_____米。‎ ‎【答案】①东、45°、1000‎ ‎②北、西、60°、800‎ ‎③南、西、15°、400‎ ‎④南、东、70°、600‎ ‎【解析】以南北为主要方向,用北偏东（西）或南偏东（西)多少度来描述。根据已知角度求出相应的角度。‎ ‎35.一根长2米的圆木，截成两段后，表面积增加48平方厘米，这根圆木原来的体积是（    ）立方厘米.‎ ‎【答案】故答案为：4800‎ ‎【解析】一根圆木截成两段后，表面积增加48平方厘米，即：增加了两个底面的面积，因此一个底面的面积为：48÷2=24平方厘米，2米=200厘米，圆木的体积为：24×200=4800立方厘米。‎ ‎36.把一张长8分米，宽5分米的白纸，围成一个圆柱形纸筒，这个纸筒的侧面积是（ ）平方分米。‎ ‎【答案】故答案为：40.‎ ‎【解析】纸筒的侧面积等于这张长方形纸的面积，即：8×5=40平方分米。‎ ‎37.从圆锥的（     ）到（           ）的距离是圆锥的高。‎ ‎【答案】故答案为：顶点；底面圆心 ‎【解析】从圆锥的顶点到底面圆心的距离就是圆锥的高，圆锥只有一条高。‎ ‎38.如图是某街区的平面图。‎ ‎(1)用数对表示医院、学校的位置。   医院(_____，_____)     学校(_____，_____)‎ ‎(2)医院在学校的_____偏__________°方向。‎ ‎(3)百货商场位置在(8，4)，请在图中标出来，它在学校的_____偏__________°方向。‎ ‎【答案】（1）2，6、6，2；（2）西、北、45；（3）东、北、45。‎ ‎【解析】数对表示位置的方法是：第一个数字表示列，第二个数字表示行，再根据上北下南左西右东的原则，由此就可以判断出医院、百货商场相对于学校的方向.由此即可解答问题。‎ ‎39.确定观测点后，知道物体的__________和__________就能确定物体的位置。‎ ‎【答案】方向，距离。‎ 19‎ ‎【解析】根据平面图上的辨别方向的方法：上北下南，左西右东以及角度和距离确定各物体的位置，即只要确定方向和距离就能够确定物体的位置 ‎40.在一个等腰三角形中，它的顶角是40°，一个底角是（       ），这个三角形也是（       ）三角形。‎ ‎【答案】70°，锐角。‎ ‎【解析】由已知等腰三角形顶角是40度，结合等腰三角形的两底角相等，根据三角形内角和是180度，用“（180-40）÷2”解答即可得到底角度数；然后根据三角形的分类进行解答即可。‎ ‎41.三角形按边分类可分为（              ）三角形、（              ）三角形、（           ）三角形。‎ ‎【答案】不等边，等腰，等边。‎ ‎【解析】根据三角形边的特点可以把三角形分为三类，分别是不等边三角形、等腰三角形和等边三角形。‎ ‎42.将一个圆锥沿着它的高平均切成两半，截面是一个（         ）形。‎ ‎【答案】三角 ‎【解析】通过实际操作可以发现把圆锥沿高切开会得到一个三角形，三角形的底是圆锥的底面直径，高是圆锥的高。‎ ‎43.火箭升空是（      ）运动现象。‎ ‎【答案】平移 ‎【解析】火箭升空只是位置发生了变化，在一定时间内，它的形状、大小不变，属于平移现象；解：火箭升空只是位置发生了变化，在一定时间内，它的形状、大小不变，属于平移现象；‎ ‎44.圆是轴对称图形，有（      ）条对称轴。‎ ‎【答案】无数 ‎【解析】圆是轴对称图形，所有经过圆心的直线都是它的对称轴，故有无数条对称轴，解：圆是轴对称图形，有无数条对称；‎ ‎45.梯形是（      ）轴对称图形。‎ ‎【答案】等腰.‎ ‎【解析】根据轴对称图形的意义判断即可.解：根据轴对称图形的意义可知：等腰梯形是轴对称图形；‎ 三、判断题 ‎46.长方体的底面积越小，它的体积就越小。（   ）‎ ‎【答案】×‎ ‎【解析】长方体的体积的大小跟底面积和高有关系，如果高不变底面积越小，体积才越小，本题没有说高的变化，因此本题错误。‎ ‎47.正方体和长方体的体积都可以用底面积乘高来进行计算。（  ）‎ ‎【答案】√‎ ‎【解析】正方体和长方体的体积都可以用底面积乘高来表示，因此本题正确。‎ ‎48.棱长是6厘米的正方体，表面积与体积相等。(    )‎ ‎【答案】×‎ ‎【解析】体积单位和面积单位，面积单位和长度单位表示的意义不同，因此无法比较它们之间的大小。所以本题错误。‎ ‎49.长方体是特殊的正方体。（  ）‎ ‎【答案】×‎ ‎【解析】正方体是特殊的长方体，而长方体不是特殊的正方体，根据此判断即可。‎ ‎50.体积相等的两个正方体，它的表面积也一定相等。（    ）‎ ‎【答案】√‎ ‎【解析】体积相等的两个正方体，棱长一定相等，它们的表面积也一定相等。‎ 19‎ ‎51.体积单位比面积单位大，面积单位比长度单位大。（     ）‎ ‎【答案】×‎ ‎【解析】体积单位、面积单位和长度单位无法比较。‎ ‎52.两个体积一样大的盒子,它们的容积一样大。(    )‎ ‎【答案】×‎ ‎【解析】容积是从里面量，体积是从外面量。两个体积一样大的盒子,它们的容积大小不能确定。‎ ‎53.一个圆柱和一个长方体等底等高，那么它们的体积也一定相等。  （  ）‎ ‎【答案】√‎ ‎【解析】圆柱和长方体的体积都可以用底面积乘高表示，它们两个等底等高，因此体积相等，所以本题正确。‎ ‎54.求一个水桶需要多少铁皮就是水桶的侧面积加上2个底面的面积。 （  ）‎ ‎【答案】×‎ ‎【解析】水桶是无盖的，因此求水桶的面积就是一个侧面的面积加上一个底面的面积。‎ ‎55.圆柱体的高越长，它的侧面积就越大。(    )‎ ‎【答案】×‎ ‎【解析】圆柱的侧面积的大小取决于两个因素，一是底面周长的大小，二是高的长短，只改变其中的一个因素，不能判断它的侧面积是大还是小。根据此判断即可。‎ ‎56.只要在四边形的对角线上加钉一根木条，这个四边形就可以固定了。（      ）‎ ‎【答案】√。‎ ‎【解析】三角形的稳定性的应用问题，正确。‎ ‎57.如果一个圆锥的体积是一个圆柱体积的，那么它们一定等底等高。（      ）‎ ‎【答案】×‎ ‎【解析】等底等高的圆柱体积是圆锥体积的3倍，但是如果一个圆锥的体积是一个圆柱体积的，这两个形体不一定等底等高，也有可能既不等底也不等高。‎ ‎58.圆锥的高和圆柱的高都有无数条。（     ）‎ ‎【答案】×‎ ‎【解析】圆锥的高是顶点到圆心的距离，这样的线段只有一条，所以错误。‎ ‎59.三角形只能有一个直角或一个钝角. （判断对错）‎ ‎【答案】√‎ ‎【解析】‎ 试题分析：依据三角形的内角和是180度，举反例即可进行判断.‎ 解：假设这个三角形中有多于1个的钝角或直角，‎ 则这个三角形的内角和一定会大于180度，‎ 所以假设不成立，在一个三角形中，只能有一个钝角或一个直角.‎ 故答案为：√.‎ ‎【点评】掌握三角形的内角和等于180度是解题的关键.‎ ‎60.同一个平面内的两条直线，不是相交就是平行..（判断对错）‎ ‎【答案】√‎ ‎【解析】‎ 试题分析：同一平面内两条直线的位置有两种：平行、相交.据此解答.‎ 解：因同一平面内两条直线的位置关系只有两种平行和相交.‎ 所以原题的说法正确.‎ 故答案为：√.‎ ‎【点评】本题考查了学生同一平面内两条直线位置关系的知识.‎ 19‎ 提升题 一、解答题 ‎61.一个长方体和一个正方体的棱长之和相等，已知长方体的长为5厘米，宽为3厘米，高为4厘米，求正方体的棱长。‎ ‎【答案】（5+3+4）×4‎ ‎=12×4‎ ‎=48（厘米）‎ ‎48÷12=4（厘米）‎ 答：正方体的棱长是4厘米。‎ ‎【解析】先求长方体的棱长总和，再求正方体的棱长。‎ ‎62.一块正方形的菜园，有一面靠墙，用长24米的篱笆围起来，这块菜地的面积是多少？‎ ‎【答案】‎ ‎24÷3=8(米)‎ ‎8×8=64(平方米)‎ 答：这块菜地的面积是64平方米。‎ ‎【解析】先求出正方形的边长，24÷3=8米，然后根据正方形的面积公式：正方形的面积＝边长×边长进行就算。‎ ‎63.压路机的滚筒是圆柱体，它的长是2米，滚筒横截面的半径是0.6米。如果每分转动5周，每分可以压多大的路面？‎ ‎【答案】解：2×3.14×0.6×2×5=3.768×2×5=7.536×5=37.68（平方米）；‎ 答：每分可以压37.68平方米的路面.‎ ‎【解析】根据圆柱的侧面积=底面周长乘高求出滚筒的侧面积，如果每分转动5周,就是5个侧面积。‎ ‎64.一个圆柱形铁皮盒，底面半径是2分米，高5分米，在这个盒子的侧面帖上商标纸，需多少平方分米的纸？‎ ‎【答案】解：2×3.14×2×5=3.14×2×2×5=3.14×20=62.8（平方分米）.‎ 答：需要62.8平方分米的纸.‎ ‎【解析】“在这个盒子的侧面帖上商标纸，需多少平方分米的纸”，就是求这个圆柱的侧面积，圆柱的侧面积=底面周长乘高，据此解答.‎ ‎65.已知一个等腰三角形的一个顶角是70°，它的每一个底角是多少度？‎ ‎【答案】55度 ‎【解析】‎ 试题分析：等腰三角形的特征：两腰相等，两底角也相等；再根据三角形内角和是180°和一个顶角是70°，先求得两个底角的度数，进而求得它的一个底角的度数.‎ 解：它的两个底角的度数和是：‎ ‎180°﹣70°=110°，‎ 它的一个底角的度数是：‎ ‎110°÷2=55°；‎ 答：它的每一个底角是55度.‎ ‎【点评】此题根据等腰三角形的特征和三角形的内角和解决.‎ ‎66.在边长为25米的正方形水池四周铺设小正方形的水泥砖，这种水泥砖每边为50厘米.如果紧靠水池边铺三层水泥砖，成为三层空心方阵，共需水泥砖多少块？‎ ‎【答案】25米=2500厘米，‎ 边所需的块数：2500÷50×4×3=600（块），‎ 角所需的块数：3×3×4=36（块），‎ 共需水泥砖的块数：600+36=636（块），‎ 19‎ 答：共需水泥砖636块.‎ ‎【解析】略 ‎67.王大伯要在墙边围一块长方形地养鸡，长28米、宽15米.这块地一边靠墙，另外三边用篱笆围.有两种围法可以选择（如图）.哪一种围法用的篱笆少些？只要多少米？‎ ‎【答案】第一种围法用的篱笆少些，只要58米.‎ ‎【解析】‎ 试题分析：第一种围法：以长边靠墙，篱笆长等于宽×2+长；第二种围法：以宽边靠墙，篱笆长等于长×2+宽，据此计算即可解答.‎ 解：第一种围法：15×2+28=58（米），‎ 第二种围法：28×2+15=71（米），‎ 答：第一种围法用的篱笆少些，只要58米.‎ ‎【点评】此题考查了长方形的周长公式的计算应用.‎ ‎68.求下列阴影部分的面积.‎ ‎【答案】9.87平方厘米；14.13平方厘米 ‎【解析】‎ 试题分析：（1）阴影部分的面积就等于梯形的面积减去半圆的面积，利用梯形的面积公式S=（a+b）h÷2和圆的面积公式S=πr2即可求解；‎ ‎（2）阴影部分的面积就等于环形面积的一半，利用环形的面积公式S=π（R2﹣r2）即可求解.‎ 解：（1）（6+10）×（6÷2）÷2﹣3.14×（6÷2）2÷2‎ ‎=16×3÷2+3.14×9÷2‎ ‎=24﹣14.13‎ ‎=9.87（平方厘米）‎ 答：阴影部分的面积是9.87平方厘米.‎ ‎（2）8÷2=4（厘米）‎ ‎4+1=5（厘米）‎ ‎3.14×（52﹣42）÷2‎ ‎=3.14×（25﹣16）÷2‎ ‎=3.14×9÷2‎ ‎=14.13（平方厘米）；‎ 答：阴影部分的面积增加14.13平方厘米.‎ ‎【点评】此题主要考查梯形、圆形和环形的面积公式的灵活应用.‎ ‎69.如图平行四边形ABCD的边BC长为10厘米，直角三角形BCE的直角边CE长为8厘米.已知两块阴影部分的面积之和比三角形EFG的面积大10平方厘米.CF长是多少厘米？‎ 19‎ ‎【答案】5厘米 ‎【解析】‎ 试题分析：“两块阴影部分的面积之和比三角形EFG的面积大10平方厘米”那么图中阴影部分面积加上中间梯形的面积（即这个平行四边形的面积）仍比三角形EFG的面积加上梯形的面积之和（即三角形BCE的面积）大10平方厘米，所以可得等量关系：平行四边形的面积=三角形BCE的面积+10平方厘米；据此解答。‎ 解：8×10÷2＝40（平方厘米）‎ ‎40+10＝50（平方厘米）‎ ‎50÷10＝5（厘米）‎ 所以CF长为5厘米.‎ ‎70.张爷爷家有一块平行四边形菜地，地的底长80米，高是50米，张爷爷准备在地中间修一条宽3米的路，修完路后，这块地实际种菜面积是多少平方米？‎ ‎【答案】3850平方米 ‎【解析】‎ 试题分析：由题意可知：实际种菜的地面是一个底和高分别为80﹣3=77米，50米的平行四边形，利用平行四边形的面积公式即可求解.‎ 解：（80﹣3）×50‎ ‎=77×50‎ ‎=3850（平方米）‎ 所以这块地实际种菜面积是3850平方米.‎ ‎71.求下列图形的面积（单位：厘米）。‎ ‎【答案】16平方厘米 ‎【解析】‎ 解：如图延长BA和CD交于E。‎ 19‎ ‎∠ABC=45°，∠DCB=90°，∠EAD=90°‎ BC=CE=6   AD=AE=2‎ ‎6×6÷2-2×2÷2‎ ‎=18-2‎ ‎=16（平方厘米）‎ 所以四边形的面积是16平方厘米。‎ ‎72.（1）请你求出梯形草坪的面积。‎ ‎（2）你知道荷花池和小路的面积分别是多少平方米吗？‎ ‎【答案】草坪625平方米；小路250平方米；荷花池125平方米 ‎【解析】‎ 试题分析：长方形面积就是它的长乘以高。这道题把小路去除，让梯形和三角形拼接起来在做计算。‎ 解：（1）（20+40-10）×25÷2 =625（平方米）；‎ ‎（2）小路：10×25= 250（平方米）；荷花池：（40-20-10）×25÷2=125（平方米）‎ ‎73.某市有一块工业园，地面形状如图，根据图上所标的长度计算这块地有多少公顷？‎ ‎【答案】12.5公顷 ‎【解析】‎ 试题分析：观察图形可知，这个工业园的面积等于上面的梯形的面积与下面的三角形的面积之和，据此根据梯形和三角形的面积公式进行计算即可解答问题.‎ 解：（200+420）×200÷2+420×300÷2‎ ‎=62000+63000‎ 19‎ ‎=125000（平方米）‎ ‎=12.5公顷 答：这块地的面积是12.5公顷.‎ ‎74.如图中的小方格是边长为1厘米的小正方形，A点用数对（2，5）表示，在图中找出用数对（4，4）表示的C点，并求出三角形ABC的面积.‎ ‎【答案】三角形ABC的面积为3平方厘米 ‎【解析】‎ 试题分析：（1）数对表示位置的方法是：第一个数字表示列，第二个数字表示行，据此即可标出C点的位置；‎ ‎（2）根据三个点的位置可以连线得到三角形ABC，然后根据三角形面积公式的求法求出面积.‎ 解：（1）根据分析，标出图后如下，并连成三角形：‎ ‎（2）根据小方格是边长为1厘米的小正方形，所以BC=3厘米，高为2厘米；‎ 所以三角形ABC的面积为：3×2÷2=3（平方厘米）；‎ 答：三角形ABC的面积为3平方厘米.‎ ‎75.长方形的宽是多少厘米？‎ ‎【答案】12.56厘米 ‎【解析】‎ 试题分析：先求出圆的半径：16÷2=8厘米，再根据圆的面积公式：S=πr2，把数据代入公 19‎ 式求出圆的面积即长方形的面积，然后根据长方形的面积公式：S=ab，求出长方形的宽即可.‎ 解：16÷2=8（厘米）‎ ‎3.14×8×8÷16‎ ‎=200.96÷16‎ ‎=12.56（厘米）‎ 答：长方形的宽是12.56厘米.‎ ‎【点评】本题考查了圆的面积公式：S=πr2，长方形的面积公式：S=ab的综合应用，本题关键是求出圆的面积即长方形的面积.‎ 二、作图题 ‎76.（1）每个方格的边长表示1厘米，以点（4，9）为圆心画一个半径2厘米的圆.‎ ‎（2）如果把这个圆先向右平移7格再向下平移5格，平移后圆心的位置用数对表示是？‎ ‎【答案】解：（1）如下图所示：‎ ‎ ‎ ‎（2）如图：‎ 19‎ ‎4+7=11，9-5=4，‎ 故平移后圆心的位置用数对表示是（11，4）‎ ‎【解析】（1）圆心确定圆的位置，半径确定圆的大小，由此以点（4，9）为圆心，以2厘米为半径画圆；‎ ‎（2）向右平移加，向下平移减，依此可得平移后圆心的位置。‎ ‎77.在下面方格纸上画出一个与已知梯形的面积相同的三角形.‎ ‎【答案】解：在下面方格纸上画出一个与已知梯形的面积相同的三角形：‎ ‎【解析】图中梯形的面积是（2+4）×3÷2=9，根据三角形的面积公式“S=ah”，画一个底为梯形上、下底之和，与梯形等高的三角形，其面积就是×6×3=9，与梯形的面积相等（画法不唯一）.‎ ‎78.（1）北京城区的西南地区下雨，用“△”在图上表示出下雨的位置.‎ ‎（2）北京城区东北方向受到冷空气袭击，用“○”在图上表示出受冷空气袭击的位置.‎ ‎（3）北京城区西面气温最高，用“□”在图中标出气温最高的位置.‎ 19‎ ‎【答案】根据分析画图如下：‎ ‎【解析】（1）北京城区的西南地区是房山，用“△”在房山上标出即可.‎ ‎（2）北京城区东北方向是顺义，用“○”在顺义上标出即可.‎ ‎（3）北京城区西面是门头沟，用“□”在门头沟上标出即可.‎ ‎79.在佳和园小区东边40米的地方有一所幼儿园，西边60米的地方有一个银行，东边50米的地方有一家超市，南边40米的地方有一家饭店.请你分别标出幼儿园、银行、超市和饭店的位置。‎ ‎【答案】40÷10=4（厘米），‎ ‎60÷10=6（厘米），‎ ‎50÷10=5（厘米），‎ 所以它们的位置如下图所示：‎ ‎【解析】因为图中1小段的距离表示实际距离10米，于是即可求出它们之间的图上距离是几小段，再据它们之间的方向关系，即可在图上标出它们各自的位置.‎ ‎80.动手画一画.‎ 19‎ ‎（1）在下面的方格纸中任意设计一个轴对称图形，并画出它的对称轴.‎ ‎（2）画出平行四边形ABCD绕D点顺时针旋转90°后的图形.‎ ‎【答案】见解析 ‎【解析】‎ 试题分析：依据轴对称图形的概念即可作答.‎ 解：如图所示，即为所要求的作图；‎ ‎.‎ ‎【点评】此题主要考查轴对称图形的概念及画法.‎ 三、计算题 ‎81.求下列各圆锥的体积：‎ ‎（1）底面周长是9.42米，高是1.8米；‎ ‎（2）底面半径是4厘米，高是21厘米；‎ ‎【答案】（1）底面半径9.42÷3.14÷2＝1.5（米）体积是1.5×1.5×3.14×1.8×＝4.239（立方米）。‎ ‎（2）351.68立方厘米 ‎【解析】圆锥的体积= 底面积高 ‎82.在三角形中，已知∠1=62°，∠2=108°，求∠3.‎ ‎【答案】∠3=10°‎ ‎【解析】‎ 试题分析：根据三角形的内角和是180度，计算出∠3的度数.‎ 解：∠3=180°﹣（∠1+∠2），‎ ‎=180°﹣（62°+108°），‎ ‎=10°.‎ 答：∠3=10°.‎ ‎【点评】解决本题的关键是根据三角形的内角和是180°计算出∠3的度数.‎ ‎83.（1）求图1的表面积和体积 ‎（2）求图2的体积 19‎ ‎【答案】图1的表面积是12.56，体积是2.7475；图2体积是314立方厘米.‎ ‎【解析】‎ 试题分析：（1）根据圆柱的表面积公式：S表面积=2πr2+2πrh，体积公式：V=πr2h，代入公式计算即可；‎ ‎（2）圆锥的体积公式：V=πr2h，代入公式计算即可.‎ 解：（1）圆柱表面积：2×3.14×0.5×3.5+3.14×0.52×2‎ ‎=10.99+1.57‎ ‎=12.56；‎ 体积：3.14×0.52×3.5‎ ‎=3.14×0.25×3.5‎ ‎=2.7475；‎ 答：图1的表面积是12.56，体积是2.7475.‎ ‎（2）×3.14×（10÷2）2×12‎ ‎=3.14×25×4‎ ‎=314（立方厘米）.‎ 答：图2体积是314立方厘米.‎ ‎【点评】此题主要考查圆柱的表面积和体积公式及圆锥的体积公式.‎ ‎84.如图空白部分的面积是20平方厘米，求阴影部分的面积.‎ ‎【答案】解：（14﹣20×2÷8）×8‎ ‎=（14﹣5）×8‎ ‎=9×8‎ ‎=72（平方厘米）‎ 答：阴影部分的面积是72平方厘米。‎ ‎【解析】阴影部分是一个平行四边形，用空白部分三角形的面积乘2再除以高求出三角形的底，用14cm减去三角形的底就是平行四边形的底，再利用平行四边形的面积公式代入数据计算即可解答。‎ ‎85.如图，阴影部分的面积是6平方厘米，求梯形的面积.‎ 19‎ ‎【答案】解：6×2÷3=4（厘米）‎ ‎5×4÷2+6‎ ‎=10+6‎ ‎=16（平方厘米）‎ 答：梯形的面积是16平方厘米。‎ ‎【解析】观察图形可知，面积是6平方厘米的三角形的底是3厘米，则根据三角形的面积公式可得这个三角形的高是6×2÷3=4（厘米），又因为空白处的三角形的底是5厘米，高等于阴影三角形的高，也是4厘米，据此求出空白处的三角形的面积，再加上阴影部分的面积即可求出梯形的面积。‎ 19‎