- 2021-06-21 发布 |
- 37.5 KB |
- 28页

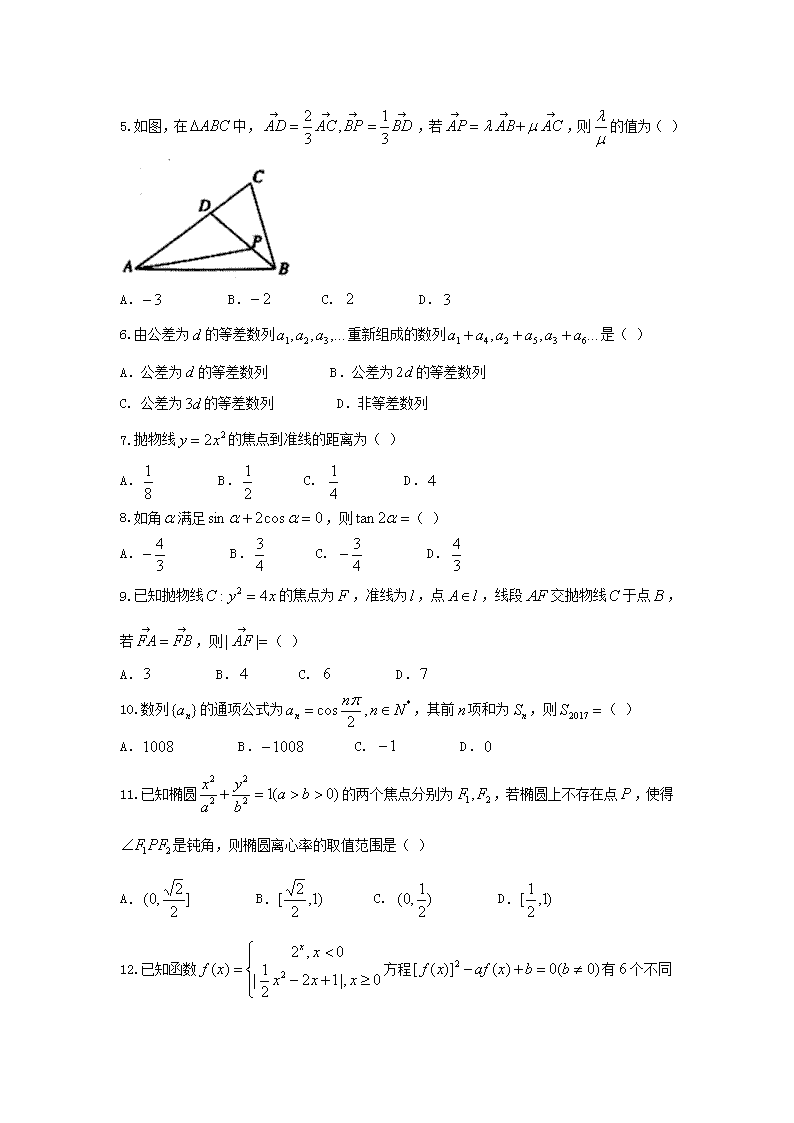

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2019届安徽省淮北一中高二上学期期中考试(2017-11)
淮北一中 2017-2018 学年高二上学期期中考试 数学(理科) 第Ⅰ卷(共 60 分) 一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选 项中,只有一项是符合题目要求的. 1.已知 ,且 ,则 的最小值为( ) A. B. C. D. 2.离心率为 ,且过点 的椭圆的标准方程是( ) A. B. 或 C. D. 或 3.在 中, ( 分别为角 的对边),则 的形状为( ) A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰三角形或直 角三角形 4.执行如图所示的程序框图,如果输出 ,则输入的 ( ) A. B. C. D. 0, >yx 211 =+ yx yx 2+ 223− 2 223− 223+ 2 223+ 2 3 )0,2( 14 2 2 =+ yx 14 2 2 =+ yx 14 2 2 =+ yx 14 22 =+ yx 14 2 2 =+ yx 1164 22 =+ yx ABC∆ c caB 22cos2 += cba ,, CBA ,, ABC∆ 9 4=S =n 3 4 5 6 5.如图,在 中, ,若 ,则 的值为( ) A. B. C. D. 6.由公差为 的等差数列 重新组成的数列 是( ) A.公差为 的等差数列 B.公差为 的等差数列 C. 公差为 的等差数列 D.非等差数列 7.抛物线 的焦点到准线的距离为( ) A. B. C. D. 8.如角 满足 ,则 ( ) A. B. C. D. 9.已知抛物线 的焦点为 ,准线为 ,点 ,线段 交抛物线 于点 , 若 ,则 ( ) A. B. C. D. 10.数列 的通项公式为 ,其前 项和为 ,则 ( ) A. B. C. D. 11.已知椭圆 的两个焦点分别为 ,若椭圆上不存在点 ,使得 是钝角,则椭圆离心率的取值范围是( ) A. B. C. D. 12.已知函数 方程 有 个不同 ABC∆ →→→→ == BDBPACAD 3 1,3 2 →→→ += ACABAP µλ µ λ 3− 2− 2 3 d ,...,, 321 aaa ...,, 635241 aaaaaa +++ d d2 d3 22xy = 8 1 2 1 4 1 4 α 0cos2sin =+ αα =α2tan 3 4− 4 3 4 3− 3 4 xyC 4: 2 = F l lA∈ AF C B →→ = FBFA = → || AF 3 4 6 7 }{ na *,2cos Nnnan ∈= π n nS =2017S 1008 1008− 1− 0 )0(12 2 2 2 >>=+ bab y a x 21, FF P 21PFF∠ ]2 2,0( )1,2 2[ )2 1,0( )1,2 1[ ≥+− < = 0|,122 1| 0,2 )( 2 xxx x xf x )0(0)()]([ 2 ≠=+− bbxafxf 6 的实根,则 取值范围( ) A. B. C. D. 第Ⅱ卷(共 90 分) 二、填空题(每题 5 分,满分 20 分,将答案填在答题纸上) 13.命题“ ”的否定是 . 14.在数列 中,已知其前 项和为 ,则 . 15.设实数 满足 ,则 的最大值为 . 16.下列命题中,假命题的序号有 . (1)“ ”是“函数 为偶函数”的充要条件; (2)“直线 垂直平面 内无数条直线”是“直线 垂直平面 ”的充分条件; (3)若 ,则 ; (4)若 ,则 . 三、解答题 (本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演 算步骤.) 17. 已知函数 . (1)当 时,解关于 的不等式 ; (2)若 ,解关于 的不等式 . 18. 设数列 满足 . (1)求 的通项公式; (2)求数列 的前 项和. 19. 已知函数 . (1) 的最小正周期和单调递增区间; (2)已知 是 三边长,且 的面积 .求角 及 ba +3 )11,6[ )11,3[ )11,6( )11,3( 02, ≥∈∃ xRx }{ na n 32 += n nS =na yx, ≤−+ ≤−+ ≥−+ 0102 0142 06 yx yx yx xy2 1−=a )(|1|)( 2 Rxaxxxf ∈+++= l a l a 0=xy 0|||| =+ yx 022,: 0 2 00 ≤++∈∃ xxRxp 022,: 2 >++∈∀¬ xxRxp 1)1()( 2 ++−= xaaxxf 2=a x 0)( ≤xf 0>a x 0)( ≤xf }{ na nanaa n 2)12(3 21 =−+++ }{ na }12{ +n an n xxxxf 2cos2)62sin()62sin()( +−++= ππ )(xf cba ,, ABC∆ ABCCf ∆= ,2)( 7,310 == cS C 的值. 20. 已知椭圆 ,其长轴为 ,短轴为 . (1)求椭圆 的方程及离心率. (2)直线 经过定点 ,且与椭圆 交于 两点,求 面积的最大值. 21. 已知数列 满足 ,且 ( 且 ). (1)求数列 的通项公式; (2)设数列 的前 项之和 ,求证: . 22. 已知过抛物线 的焦点 ,斜率为 的直线交抛物线于 两点,且 . (1)求该抛物线 的方程; (2)已知抛物线上一点 ,过点 作抛物线的两条弦 和 ,且 , 判断直线 是否过定点?并说明理由. ba, )0(1: 2 2 2 2 >>=+ bab y a xC 4 2 C l )2,0( C BA, OAB∆ }{ na 11 =a n nn aa 22 1 += − 2≥n *Nn∈ }{ na }{ na n nS 322 −> nS n n )0(2: 2 >= ppxyC F 2 ))(,(),,( 212211 xxyxByxA < 6|| =AB C )4,(tM M MD ME MEMD ⊥ DE 淮北一中 2017-2018 学年高二上学期期中考试数学(理科) 参考答案 1.D 【解析】由 得, ,因为 ,,所以 (当且仅当 时等 号成立),故选 D. 【易错点晴】本题主要考查利用基本不等式求最值,属于中档题.利用基本不等式求最值时, 一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正; 二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要 验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用 或 时 等号能否同时成立). 2.D 【解析】当椭圆的焦点在 x 轴上,设椭圆的方程为 ,由离心率为 ,∴ ∵椭圆过点(2,0),∴ ,∴a2=4,∴b2=1, ∴椭圆标准方程为 当椭圆的焦点在 y 轴上,同理易得: 故选 D. 3.A 【解析】 , ,解得 ,即角 C 为直角,则 的形状为直角三角形,故选 A. 4.B 【解析】该程序框图表示的是通项为 的前 项和, , 输出结果为 , 2 1 coscos 2 2 2 B B a c c + += = 2 2 2 cos 2 a c b aB ac c + −∴ = = 2 2 2a b c+ = ABC∆ ( )( ) ( )( ) 1 1 1 2 1 2 1 2 2 1 2 1na n n n n = = − + − + n 1 1 1 1 1 11 ...2 3 3 5 2 1 2 1nS n n = − + − + + − − + 1 112 2 1 2 1 n n n = − = + + 4 9 ,得 ,故选 B. 5.D 【解析】 , , 又 , ,故选 D. 6.B 【 解 析 】 设 新 数 列 的 第 项 是 , 则 , , 此新数列是以 为公 差的等差数列,故选 B. 【方法点晴】本题主要考查等差数列的定义、等差数列通项公式,属于难题.判定一个数列 为等差数列的常见方法是:(1) 定义法: ( 是常数),则数列 是等差数 列(2) 等差中项法: ( ),则数列 是等差数列;(3) 通项公式: ( 为常数), 则数列 是等差数列;(4) 前 n 项和公式: ( 为常数) , 则数列 是等差数列.本题先利用方法(1)判定出数列 是等差数列后 再进行解答的. 7.C 【解析】由 得: ,所以 , ,即焦点到准线的距离为 , 故选 C. 8.D 【解析】由题意可得 ,选 D. 9.B 【解析】 4 2 1 9 n n ∴ =+ 4n = 1 4 2 5 3 6, , ...a a a a a a+ + + n nb 3n n nb a a += + = ( ) ( ) ( )1 12 1 2 2 2 1a n d n d a n d+ − + + = + + 1 2n nb b d+∴ − = ∴ 2d 1n na a d+ − = d { }na 1 +22 = +n n na a a+ *n N∈ { }na =na pn q+ ,p q { }na 2 nS An Bn= + ,A B { }na { }na 22y x= 2 1 2x y= 12 2p = 1 4p = 1 4p = 由已知 为 的三等分,作 于 ,如图,则 , ,故选 B. 10.D 【解析】 选 D. 11.A 【 解 析 】 设 B 为 短 轴 端 点 , 则 , 由 题 意 得 ,选 A。 12.D 【解析】由题意可画出 y=f(x)的图像如下图,f(0)=1,f(2)=1,注意 y=1 是图像的一条渐近 线,令 t=f(x), ,由图像可知, 当 时,方程 f(x)=t 有 4 个解,当 和 时,方程 f(x)=t 有 2 个解, 当 时,方程 f(x)=t 有 1 个解,当 t=1 时,方程 f(x)=t 有 3 个解 当 t<0 时,方程 f(x)=t 有 0 个解 复 合 方 程 有 6 个 根 , 一 定 是 4+2 , 即 , 的 两 个 根 分 别 在 , 令 , 所 以 ,由线性规划可求得 ,选 D. 【点睛】 复合方程根的问题,一般先画出内函数的图像,分析 t=f(x),t 的不同取值根的情况,再由 此分析外函数根的情况,从而解决问题。 13. 【解析】含有存在量词的命题的否定是含有全称量词的命题,命题“∃x∈R,2x≥0”的否定 是 . B AF BH l⊥ H 2 4 4,3 3 3BH FK BF BH= = ∴ = = 3 4AF BF∴ = = 4 1 2 3 4 2017 14, 0 504 0n n T Ta a T S a a a a S S a+ = ∴ = = + + + = ∴ = + = 1 2 1 2F PF F BF∠ ≤ ∠ 2 2 2 1 2 π 21 02 2 cF BF c a c eb ∠ ≤ ⇒ ≤ ⇒ ≤ − ⇒ < ≤ ( )2 0 0t at b b− + = ≠ 0 1t< < 1 2t< < 0t = 2t ≥ ( )2 0 0t at b b− + = ≠ 1 20 1,1 2t t< < < < ( ) ( )2 0g t t at b b= − + ≠ ( ) ( ) ( ) 0 0 { 1 1 0 , 2 4 2 0 g b g a b g a b = > = − + < = − + > 3z a b= + ( )3,11z ∈ ,2 0xx R∀ ∈ < ,2 0xx R∀ ∈ < 14. 【解析】当 时, ; 当 时, ,不满足上式。 故 。 答案: 点睛:数列的通项 an 与前 n 项和 Sn 的关系是 an= 当 n=1 时,a1 若适合 Sn- Sn-1,则 n=1 的情况可并入 n≥2 时的通项 an;当 n=1 时,a1 若不适合 Sn-Sn-1,则用分 段函数的形式表示. 15.【解析】不等式组的图象如图 由 图 象 知 , 则 , 当 且 仅 当 时,等号成立,经检验 在可行域内,故 的最大值为 25. 16.(2)(3) 【解析】(1)若“函数 为偶函数”,则 , 即 ,则 , 平方得 , ( ) ( )1 5 1{ 2 2n n na n− == ≥ 2n ≥ ( ) ( )1 1 1 2 3 2 3 2n n n n n na S S − − −= − = + − + = 1n = 1 1 2 3 5a S= = + = 1 5, 1{ 2 , 2n n na n− == ≥ 1 5, 1{ 2 , 2n n na n− == ≥ ( ) ( )2 1f x x x a x R= + + + ∈ ( ) ( )f x f x− = 2 21 1x x a x x a+ + + = + − + + ( )1 1x a x a+ + = − + ( ) ( ) ( ) ( )2 22 22 1 1 2 1 1x a x a x a x a+ + + + = − + + + 即 ,则 ,即 , 则“ ”是“函数 为偶函数”的充要条件;正确; (2)“直线 垂直平面 内无数条直线”则“直线 垂直平面 ”不一定成立,故(2)错 误; (3)当 时,满足 ,但 不成立,故(3)错误; (4)若 : ,则 : 正确. 故答案为:(2)(3) 17 .( 1 ) ( 2 ) 当 时 解 集 为 当 时 解 集 为 当 时解集为 【解析】 试题分析:(1)将 代入结合函数图像求解不等式即可;(2)解不等式要结合二次函 数图像及性质,并对两零点 大小分情况讨论 试题解析:(1)当 时得 ,解 集为 (2)∵不等式 , 当 时,有 ,∴不等式的解集为 ; 当 时,有 ,∴不等式的解集为 ; 当 时,不等式的解集为 . 考点:一元二次不等式解法及分情况讨论 18.(1) (2) 【解析】试题分析: 利用数列递推关系即可得出。 ,利用裂项求和方法即可得出。 解析:(1)数列{an}满足 a1+3a2+…+(2n﹣1)an=2n. n≥2 时,a1+3a2+…+(2n﹣3)an﹣1=2(n﹣1). 10 << a 1>a 1=a 0>a 10 << a 1>a 1=a ( ) ( )2 1 2 1a x a x+ = − + ( )4 1 0a + = 1a = − 1a = − ( ) ( )2 1f x x x a x R= + + + ∈ l α l α 0, 1x y= = 0xy = 0x y+ = p 2, 2 2 0x R x x∃ ∈ + + ≤ p¬ 2, 2 2 0x R x x∀ ∈ + + > 1[ ,2]2 {1} 2a = 1,a a 2a = ( )2 1 1 12 1 0 2 0 22 2 2x x x x x − + + ≤ ∴ − − ≤ ∴ ≤ ≤ 1[ ,2]2 {1} ∴(2n﹣1)an=2.∴an= . 当 n=1 时,a1=2,上式也成立. ∴an= . (2) = = ﹣ . ∴数列{ }的前 n 项和= + +…+ =1﹣ = . 点 睛 : 求 数 列 的 通 项 时 , 可 以 运 用 , 本 题 的 条 件 左 边 可 以 看 成 和 的 形 式 , 遇 到 ,的形式时,利用裂项求和方法即可得出结果。 19.(1)π,函数 f(x)的递增区间是[﹣ +kπ, +kπ],k∈Z;(2) a=8,b=5 或 a=5,b=8. 【解析】试题分析: 解析式利用两角和与差的正弦函数公式及二倍角的余弦函数公 式化简,整理为一个角的正弦函数,找出 的值代入周期公式即可求出 的最小正周期, 利用正弦函数的单调性即可求出 的单调递增区间。 由 ,根据第一问确定出的解析式求出 的度数,利用三角形面积公式列出关 系式,将 值代入求出 的值,利用余弦定理列出关系式,将 代入求出 的 值,联立即可求出 的值。 解析:(Ⅰ)f(x)=sin2xcos +cos2xsin +sin2xcos ﹣cos2xsin +cos2x+1= sin2x+cos2x+1=2sin(2x+ )+1, ∵ω=2,∴T= =π; 令﹣ +2kπ≤2x+ ≤ +2kπ,k∈Z,得到﹣ +kπ≤x≤ +kπ,k∈Z, 则函数 f(x)的递增区间是[﹣ +kπ, +kπ],k∈Z; (Ⅱ)由 f(C)=2,得到 2sin(2C+ )+1=2,即 sin(2C+ )= , 3 π 6 π ( ) ( )1 f x ω ( )f x ( )f x ( )2 ( ) 2f c = C sinC ab cosC a b+ ,a b ∴2C+ = 或 2C+ = , 解得:C=0(舍去)或 C= , ∵S=10 , ∴ absinC= ab=10 ,即 ab=40①, 由余弦定理得:c2=a2+b2﹣2abcosC,即 49=a2+b2﹣ab, 将 ab=40 代入得:a2+b2=89②, 联立①②解得:a=8,b=5 或 a=5,b=8. 20.(1) ,离心率: .(2)1 【解析】试题分析:(1)根据条件可得 , 即得椭圆 的方程,及离心率.(2) 先设直线方程为: ,与椭圆联立方程组,利用韦达定理,结合弦长公式求得底边 边长 ,再根据点到直线距离得高,根据三角形面积公式表示 面积,最后根据基本 不等式求最大值 试题解析:解:(Ⅰ) , , , ∴椭圆 的方程为: ,离心率: . (Ⅱ)依题意知直线的斜率存在,设直线的斜率为 ,则直线方程为: , 由 ,得 , , 由 得: , 设 , ,则 , , , 又∵原点 到直线的距离 , ∴ . 当且仅当 ,即 时,等号成立, 此时 面积的最大值为 . 点睛:解析几何中的最值是高考的热点,在圆锥曲线的综合问题中经常出现,求解此类问题 的一般思路为在深刻认识运动变化的过程之中,抓住函数关系,将目标量表示为一个(或者 多个)变量的函数,然后借助于函数最值的探求来使问题得以解决. 21.(1) an= ;(2)证明见解析. 【解析】试题分析:(1)由 ,可得 ,即 ,可得出 { }为等差数列.最终可求出{an}的通项公式.(2)采用错位相减法求出 ,再变形即可求证. (1)∵an=2an﹣1+2n(≥2,且 n∈N)∴ ∴ ∴数列{ }是以 为首项,1 为公差的等差数列; ∴an= ; (2)∵Sn= ∴2Sn= 两式相减可得﹣Sn=1+22+23+…+2n﹣ =(3﹣2n)•2n﹣3 ∴Sn=(2n﹣3)•2n+3>(2n﹣3)•2n ∴ . 点睛:在求解数列的通项公式时要注意变形及整体思想的使用,将一般数列转化为等差或等 比数列,从而求出数列通项公式。应用错位相减法求解数列的前 n 项和两式相减时要注意前 后符号的变化. 22.(1) (2) 【解析】试题分析:(1)利用点斜式设直线直线 的方程,与抛物线联立方程组,结合韦 达定理与弦长公式求 ,再根据 解得 .(2)先设直线 方程 , 与抛物线联立方程组,结合韦达定理化简 ,得 或 ,代入 12 2n n na a −= + 1 1 12 2 n n n n a a − −= + 1 1 12 2 n n n n a a − −− = 2 n n a nS 1 1 12 2 n n n n a a − −= + 1 1 12 2 n n n n a a − −− = 2 n n a 1 2 ( )1 112 2 2 n n a n n= + − = − 1 22 nn − 1 21 3 12 2 22 2 2 nn + +…+ − 2 3 11 3 12 2 22 2 2 nn + + +…+ − 11 22 nn + − 2 3nS nn > − 2 4y x= ( )8, 4− AB AB 6AB = 2p = DE x my t= + MD ME⊥ 4 8t m= + 4 4t m= − + 方程可得直线 过定点 试题解析:(1)拋物线的焦点 ,∴直线 的方程为: . 联立方程组 ,消元得: , ∴ . ∴ 解得 . ∴抛物线 的方程为: . (2)由(1)可得点 ,可得直线 的斜率不为 0, 设直线 的方程为: , 联立 ,得 , 则 ①. 设 ,则 . ∵ 即 ,得: , ∴ ,即 或 , DE DE ( )8, 4− ,02 pF AB 2 2 py x = − 2 2 { 2 2 y px py x = = − 2 2 2 04 px px− + = 2 1 2 1 22 , 4 px x p x x+ = = ( )2 2 2 1 2 1 21 2 4 3 4 6AB x x x x p p= + + − = ⋅ − = 2p = C 2 4y x= ( )4,4M DE DE x my t= + 2{ 4 x my t y x = + = 2 4 4 0y my t− − = 216 16 0m t∆ = + > ( ) ( )1 1 2 2, , ,D x y E x y 1 2 1 24 , 4y y m y y t+ = = − ( ) ( )1 1 2 24, 4 4, 4MD ME x y x y⋅ = − − ⋅ − − ( ) ( )1 2 1 2 1 2 1 24 16 4 16x x x x y y y y= − + + + − + + ( )2 2 2 2 1 2 1 2 1 2 1 24 16 4 164 4 4 4 y y y y y y y y = ⋅ − + + + − + + ( ) ( ) ( ) 2 21 2 1 2 1 2 1 23 4 3216 y y y y y y y y= − + + − + + 2 216 12 32 16 0t m t m= − − + − = 2 212 32 16 16t t m m− + = + ( ) ( )2 26 4 2 1t m− = + ( )6 2 2 1t m− = ± + 4 8t m= + 4 4t m= − + 代人①式检验均满足 , ∴直线 的方程为: 或 . ∴直线过定点 (定点 不满足题意,故舍去). 点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多 少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值 问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推 理,到最后必定参数统消,定点、定值显现. 0∆ > DE ( )4 8 4 8x my m m y= + + = + + ( )4 4x m y= − + ( )8, 4− ( )4,4 淮北一中 2017-2018 学年高二上学期期中考试数学(理科) 参考答案 1.D 【解析】由 得, ,因为 ,,所以 (当且仅当 时等 号成立),故选 D. 【易错点晴】本题主要考查利用基本不等式求最值,属于中档题.利用基本不等式求最值时, 一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正; 二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要 验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用 或 时 等号能否同时成立). 2.D 【解析】当椭圆的焦点在 x 轴上,设椭圆的方程为 ,由离心率为 ,∴ ∵椭圆过点(2,0),∴ ,∴a2=4,∴b2=1, ∴椭圆标准方程为 当椭圆的焦点在 y 轴上,同理易得: 故选 D. 3.A 【解析】 , ,解得 ,即角 C 为直角,则 的形状为直角三角形,故选 A. 4.B 【解析】该程序框图表示的是通项为 的前 项和, , 输出结果为 , 2 1 coscos 2 2 2 B B a c c + += = 2 2 2 cos 2 a c b aB ac c + −∴ = = 2 2 2a b c+ = ABC∆ ( )( ) ( )( ) 1 1 1 2 1 2 1 2 2 1 2 1na n n n n = = − + − + n 1 1 1 1 1 11 ...2 3 3 5 2 1 2 1nS n n = − + − + + − − + 1 112 2 1 2 1 n n n = − = + + 4 9 ,得 ,故选 B. 5.D 【解析】 , , 又 , ,故选 D. 6.B 【 解 析 】 设 新 数 列 的 第 项 是 , 则 , , 此新数列是以 为公 差的等差数列,故选 B. 【方法点晴】本题主要考查等差数列的定义、等差数列通项公式,属于难题.判定一个数列 为等差数列的常见方法是:(1) 定义法: ( 是常数),则数列 是等差数 列(2) 等差中项法: ( ),则数列 是等差数列;(3) 通项公式: ( 为常数), 则数列 是等差数列;(4) 前 n 项和公式: ( 为常数) , 则数列 是等差数列.本题先利用方法(1)判定出数列 是等差数列后 再进行解答的. 7.C 【解析】由 得: ,所以 , ,即焦点到准线的距离为 , 故选 C. 8.D 【解析】由题意可得 ,选 D. 9.B 【解析】 4 2 1 9 n n ∴ =+ 4n = 1 4 2 5 3 6, , ...a a a a a a+ + + n nb 3n n nb a a += + = ( ) ( ) ( )1 12 1 2 2 2 1a n d n d a n d+ − + + = + + 1 2n nb b d+∴ − = ∴ 2d 1n na a d+ − = d { }na 1 +22 = +n n na a a+ *n N∈ { }na =na pn q+ ,p q { }na 2 nS An Bn= + ,A B { }na { }na 22y x= 2 1 2x y= 12 2p = 1 4p = 1 4p = 由已知 为 的三等分,作 于 ,如图,则 , ,故选 B. 10.D 【解析】 选 D. 11.A 【 解 析 】 设 B 为 短 轴 端 点 , 则 , 由 题 意 得 ,选 A。 12.D 【解析】由题意可画出 y=f(x)的图像如下图,f(0)=1,f(2)=1,注意 y=1 是图像的一条渐近 线,令 t=f(x), ,由图像可知, 当 时,方程 f(x)=t 有 4 个解,当 和 时,方程 f(x)=t 有 2 个解, 当 时,方程 f(x)=t 有 1 个解,当 t=1 时,方程 f(x)=t 有 3 个解 当 t<0 时,方程 f(x)=t 有 0 个解 复 合 方 程 有 6 个 根 , 一 定 是 4+2 , 即 , 的 两 个 根 分 别 在 , 令 , 所 以 ,由线性规划可求得 ,选 D. 【点睛】 复合方程根的问题,一般先画出内函数的图像,分析 t=f(x),t 的不同取值根的情况,再由 此分析外函数根的情况,从而解决问题。 13. 【解析】含有存在量词的命题的否定是含有全称量词的命题,命题“∃x∈R,2x≥0”的否定 是 . B AF BH l⊥ H 2 4 4,3 3 3BH FK BF BH= = ∴ = = 3 4AF BF∴ = = 4 1 2 3 4 2017 14, 0 504 0n n T Ta a T S a a a a S S a+ = ∴ = = + + + = ∴ = + = 1 2 1 2F PF F BF∠ ≤ ∠ 2 2 2 1 2 π 21 02 2 cF BF c a c eb ∠ ≤ ⇒ ≤ ⇒ ≤ − ⇒ < ≤ ( )2 0 0t at b b− + = ≠ 0 1t< < 1 2t< < 0t = 2t ≥ ( )2 0 0t at b b− + = ≠ 1 20 1,1 2t t< < < < ( ) ( )2 0g t t at b b= − + ≠ ( ) ( ) ( ) 0 0 { 1 1 0 , 2 4 2 0 g b g a b g a b = > = − + < = − + > 3z a b= + ( )3,11z ∈ ,2 0xx R∀ ∈ < ,2 0xx R∀ ∈ < 14. 【解析】当 时, ; 当 时, ,不满足上式。 故 。 答案: 点睛:数列的通项 an 与前 n 项和 Sn 的关系是 an= 当 n=1 时,a1 若适合 Sn- Sn-1,则 n=1 的情况可并入 n≥2 时的通项 an;当 n=1 时,a1 若不适合 Sn-Sn-1,则用分 段函数的形式表示. 15.【解析】不等式组的图象如图 由 图 象 知 , 则 , 当 且 仅 当 时,等号成立,经检验 在可行域内,故 的最大值为 25. 16.(2)(3) 【解析】(1)若“函数 为偶函数”,则 , 即 ,则 , 平方得 , ( ) ( )1 5 1{ 2 2n n na n− == ≥ 2n ≥ ( ) ( )1 1 1 2 3 2 3 2n n n n n na S S − − −= − = + − + = 1n = 1 1 2 3 5a S= = + = 1 5, 1{ 2 , 2n n na n− == ≥ 1 5, 1{ 2 , 2n n na n− == ≥ ( ) ( )2 1f x x x a x R= + + + ∈ ( ) ( )f x f x− = 2 21 1x x a x x a+ + + = + − + + ( )1 1x a x a+ + = − + ( ) ( ) ( ) ( )2 22 22 1 1 2 1 1x a x a x a x a+ + + + = − + + + 即 ,则 ,即 , 则“ ”是“函数 为偶函数”的充要条件;正确; (2)“直线 垂直平面 内无数条直线”则“直线 垂直平面 ”不一定成立,故(2)错 误; (3)当 时,满足 ,但 不成立,故(3)错误; (4)若 : ,则 : 正确. 故答案为:(2)(3) 17 .( 1 ) ( 2 ) 当 时 解 集 为 当 时 解 集 为 当 时解集为 【解析】 试题分析:(1)将 代入结合函数图像求解不等式即可;(2)解不等式要结合二次函 数图像及性质,并对两零点 大小分情况讨论 试题解析:(1)当 时得 ,解 集为 (2)∵不等式 , 当 时,有 ,∴不等式的解集为 ; 当 时,有 ,∴不等式的解集为 ; 当 时,不等式的解集为 . 考点:一元二次不等式解法及分情况讨论 18.(1) (2) 【解析】试题分析: 利用数列递推关系即可得出。 ,利用裂项求和方法即可得出。 解析:(1)数列{an}满足 a1+3a2+…+(2n﹣1)an=2n. n≥2 时,a1+3a2+…+(2n﹣3)an﹣1=2(n﹣1). 10 << a 1>a 1=a 0>a 10 << a 1>a 1=a ( ) ( )2 1 2 1a x a x+ = − + ( )4 1 0a + = 1a = − 1a = − ( ) ( )2 1f x x x a x R= + + + ∈ l α l α 0, 1x y= = 0xy = 0x y+ = p 2, 2 2 0x R x x∃ ∈ + + ≤ p¬ 2, 2 2 0x R x x∀ ∈ + + > 1[ ,2]2 {1} 2a = 1,a a 2a = ( )2 1 1 12 1 0 2 0 22 2 2x x x x x − + + ≤ ∴ − − ≤ ∴ ≤ ≤ 1[ ,2]2 {1} ∴(2n﹣1)an=2.∴an= . 当 n=1 时,a1=2,上式也成立. ∴an= . (2) = = ﹣ . ∴数列{ }的前 n 项和= + +…+ =1﹣ = . 点 睛 : 求 数 列 的 通 项 时 , 可 以 运 用 , 本 题 的 条 件 左 边 可 以 看 成 和 的 形 式 , 遇 到 ,的形式时,利用裂项求和方法即可得出结果。 19.(1)π,函数 f(x)的递增区间是[﹣ +kπ, +kπ],k∈Z;(2) a=8,b=5 或 a=5,b=8. 【解析】试题分析: 解析式利用两角和与差的正弦函数公式及二倍角的余弦函数公 式化简,整理为一个角的正弦函数,找出 的值代入周期公式即可求出 的最小正周期, 利用正弦函数的单调性即可求出 的单调递增区间。 由 ,根据第一问确定出的解析式求出 的度数,利用三角形面积公式列出关 系式,将 值代入求出 的值,利用余弦定理列出关系式,将 代入求出 的 值,联立即可求出 的值。 解析:(Ⅰ)f(x)=sin2xcos +cos2xsin +sin2xcos ﹣cos2xsin +cos2x+1= sin2x+cos2x+1=2sin(2x+ )+1, ∵ω=2,∴T= =π; 令﹣ +2kπ≤2x+ ≤ +2kπ,k∈Z,得到﹣ +kπ≤x≤ +kπ,k∈Z, 则函数 f(x)的递增区间是[﹣ +kπ, +kπ],k∈Z; (Ⅱ)由 f(C)=2,得到 2sin(2C+ )+1=2,即 sin(2C+ )= , 3 π 6 π ( ) ( )1 f x ω ( )f x ( )f x ( )2 ( ) 2f c = C sinC ab cosC a b+ ,a b ∴2C+ = 或 2C+ = , 解得:C=0(舍去)或 C= , ∵S=10 , ∴ absinC= ab=10 ,即 ab=40①, 由余弦定理得:c2=a2+b2﹣2abcosC,即 49=a2+b2﹣ab, 将 ab=40 代入得:a2+b2=89②, 联立①②解得:a=8,b=5 或 a=5,b=8. 20.(1) ,离心率: .(2)1 【解析】试题分析:(1)根据条件可得 , 即得椭圆 的方程,及离心率.(2) 先设直线方程为: ,与椭圆联立方程组,利用韦达定理,结合弦长公式求得底边 边长 ,再根据点到直线距离得高,根据三角形面积公式表示 面积,最后根据基本 不等式求最大值 试题解析:解:(Ⅰ) , , , ∴椭圆 的方程为: ,离心率: . (Ⅱ)依题意知直线的斜率存在,设直线的斜率为 ,则直线方程为: , 由 ,得 , , 由 得: , 设 , ,则 , , , 又∵原点 到直线的距离 , ∴ . 当且仅当 ,即 时,等号成立, 此时 面积的最大值为 . 点睛:解析几何中的最值是高考的热点,在圆锥曲线的综合问题中经常出现,求解此类问题 的一般思路为在深刻认识运动变化的过程之中,抓住函数关系,将目标量表示为一个(或者 多个)变量的函数,然后借助于函数最值的探求来使问题得以解决. 21.(1) an= ;(2)证明见解析. 【解析】试题分析:(1)由 ,可得 ,即 ,可得出 { }为等差数列.最终可求出{an}的通项公式.(2)采用错位相减法求出 ,再变形即可求证. (1)∵an=2an﹣1+2n(≥2,且 n∈N)∴ ∴ ∴数列{ }是以 为首项,1 为公差的等差数列; ∴an= ; (2)∵Sn= ∴2Sn= 两式相减可得﹣Sn=1+22+23+…+2n﹣ =(3﹣2n)•2n﹣3 ∴Sn=(2n﹣3)•2n+3>(2n﹣3)•2n ∴ . 点睛:在求解数列的通项公式时要注意变形及整体思想的使用,将一般数列转化为等差或等 比数列,从而求出数列通项公式。应用错位相减法求解数列的前 n 项和两式相减时要注意前 后符号的变化. 22.(1) (2) 【解析】试题分析:(1)利用点斜式设直线直线 的方程,与抛物线联立方程组,结合韦 达定理与弦长公式求 ,再根据 解得 .(2)先设直线 方程 , 与抛物线联立方程组,结合韦达定理化简 ,得 或 ,代入 12 2n n na a −= + 1 1 12 2 n n n n a a − −= + 1 1 12 2 n n n n a a − −− = 2 n n a nS 1 1 12 2 n n n n a a − −= + 1 1 12 2 n n n n a a − −− = 2 n n a 1 2 ( )1 112 2 2 n n a n n= + − = − 1 22 nn − 1 21 3 12 2 22 2 2 nn + +…+ − 2 3 11 3 12 2 22 2 2 nn + + +…+ − 11 22 nn + − 2 3nS nn > − 2 4y x= ( )8, 4− AB AB 6AB = 2p = DE x my t= + MD ME⊥ 4 8t m= + 4 4t m= − + 方程可得直线 过定点 试题解析:(1)拋物线的焦点 ,∴直线 的方程为: . 联立方程组 ,消元得: , ∴ . ∴ 解得 . ∴抛物线 的方程为: . (2)由(1)可得点 ,可得直线 的斜率不为 0, 设直线 的方程为: , 联立 ,得 , 则 ①. 设 ,则 . ∵ 即 ,得: , ∴ ,即 或 , DE DE ( )8, 4− ,02 pF AB 2 2 py x = − 2 2 { 2 2 y px py x = = − 2 2 2 04 px px− + = 2 1 2 1 22 , 4 px x p x x+ = = ( )2 2 2 1 2 1 21 2 4 3 4 6AB x x x x p p= + + − = ⋅ − = 2p = C 2 4y x= ( )4,4M DE DE x my t= + 2{ 4 x my t y x = + = 2 4 4 0y my t− − = 216 16 0m t∆ = + > ( ) ( )1 1 2 2, , ,D x y E x y 1 2 1 24 , 4y y m y y t+ = = − ( ) ( )1 1 2 24, 4 4, 4MD ME x y x y⋅ = − − ⋅ − − ( ) ( )1 2 1 2 1 2 1 24 16 4 16x x x x y y y y= − + + + − + + ( )2 2 2 2 1 2 1 2 1 2 1 24 16 4 164 4 4 4 y y y y y y y y = ⋅ − + + + − + + ( ) ( ) ( ) 2 21 2 1 2 1 2 1 23 4 3216 y y y y y y y y= − + + − + + 2 216 12 32 16 0t m t m= − − + − = 2 212 32 16 16t t m m− + = + ( ) ( )2 26 4 2 1t m− = + ( )6 2 2 1t m− = ± + 4 8t m= + 4 4t m= − + 代人①式检验均满足 , ∴直线 的方程为: 或 . ∴直线过定点 (定点 不满足题意,故舍去). 点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多 少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值 问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推 理,到最后必定参数统消,定点、定值显现. 0∆ > DE ( )4 8 4 8x my m m y= + + = + + ( )4 4x m y= − + ( )8, 4− ( )4,4查看更多