数学理卷·2019届湖北省天门中学高二10月月考（2017-10）

数学理卷·2019届湖北省天门中学高二10月月考（2017-10）

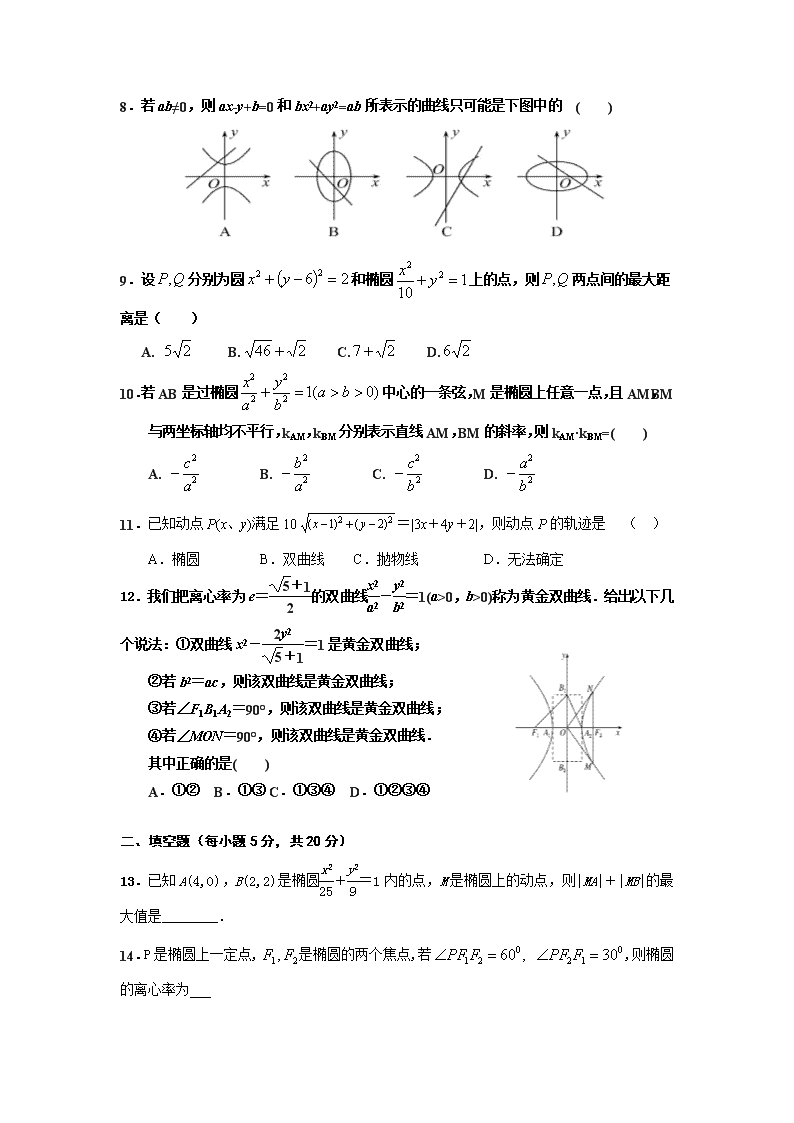
‎2017年天门中学高二保送班上学期十月考试 数学试卷(理科)‎ ‎ 命题：李会军 审题:李堃 黄兵 一、选择题（每小题5分，共60分）‎ ‎1．椭圆的焦距为2，则的值等于　（ ）.‎ ‎　　　A．5 B．8 C．5或3 D．5或8‎ ‎2．若方程x2+ky2=2表示焦点在y轴上的椭圆，那么实数k的取值范围是　(　　) ‎ A．(0，+∞) B．(0，2) C．(1，+∞) D．(0，1)‎ ‎3．若双曲线E：的左、右焦点分别为F1、F2，点P在双曲线E上，且|PF1|=7，则|PF2|等于　(　　)‎ A．13或1 B．1 C．13 D．以上都不对 ‎4．已知命题p：x∈R，2x2+2x+<0，命题q： x0∈R，sinx0-cosx0=，则下列判断中正确的是　(　　)‎ A．p是真命题 B．q是假命题 C．p是假命题 D． q是假命题 ‎5．F1、F2是椭圆＋＝1(a>b>0)的两焦点，P是椭圆上任一点，过一焦点引∠F1PF2的外角平分线的垂线，则垂足Q的轨迹为(　　)‎ A．圆　　　　　　B．椭圆　　　　C．双曲线　　　　　D．抛物线 ‎6．过双曲线x2－y2＝8的左焦点F1有一条弦PQ在左支上，若|PQ|＝7，F2是双曲线的右焦点，则△PF2Q的周长是(　)‎ A．28　　 B．14－8 C．14＋8 D．8 ‎7．圆上到直线的距离等于的点共有（ ）‎ A．1个 B．2个 C．3个 D．4个 ‎8．若ab≠0，则ax-y+b=0和bx2+ay2=ab所表示的曲线只可能是下图中的　(　　)‎ 9． 设分别为圆和椭圆上的点，则两点间的最大距　　离是（ ）‎ ‎ A. B. C. D.‎ ‎10．若AB是过椭圆中心的一条弦，M是椭圆上任意一点，且AM，BM与两坐标轴均不平行，kAM，kBM分别表示直线AM，BM的斜率，则kAM·kBM=(　　)‎ A. B. C. D. ‎ ‎11．已知动点P(x、y)满足10＝|3x＋4y＋2|，则动点P的轨迹是 （ ）‎ ‎ A．椭圆 B．双曲线 C．抛物线 D．无法确定 ‎12．我们把离心率为e＝的双曲线－＝1(a>0，b>0)称为黄金双曲线．给出以下几个说法：①双曲线x2－＝1是黄金双曲线；‎ ‎②若b2＝ac，则该双曲线是黄金双曲线；‎ ‎③若∠F1B1A2＝90°，则该双曲线是黄金双曲线；‎ ‎④若∠MON＝90°，则该双曲线是黄金双曲线．‎ 其中正确的是(　　)‎ A．①② B．①③ C．①③④ D．①②③④‎ 二、填空题（每小题5分，共20分）‎ ‎13．已知A(4,0)，B(2,2)是椭圆＋＝1内的点，M是椭圆上的动点，则|MA|＋|MB|的最大值是________．‎ ‎14．P是椭圆上一定点,是椭圆的两个焦点,若,则椭圆的离心率为 ‎ ‎15．已知双曲线x2－＝1的左顶点为A1，右焦点为F2，P为双曲线右支上一点，则·‎ 的最小值为________‎ ‎16．已知点P是双曲线－＝1上除顶点外的任意一点，F1、F2分别为左、右焦点，c为半焦距，△PF1F2的内切圆与F1F2切于点M，则|F1M|·|F2M|＝_______.‎ 三、解答题（共70分）‎ ‎17. （本小题满分10分）‎ 已知命题p：方程表示焦点在y轴上的椭圆，命题q：双曲线的离心率，若只有一个为真，求实数的取值范围．‎ ‎1８.（本小题满分1２分）‎ 椭圆E经过点A(2,3)，对称轴为坐标轴，焦点F1，F2在x轴上，离心率e＝.‎ ‎(1)求椭圆E的方程；‎ ‎(2)求∠F1AF2的角平分线所在直线的方程．‎ ‎19. （本小题满分12分）‎ 双曲线的中心在原点，右焦点为，渐近线方程为 .‎ ‎(1)求双曲线的方程；‎ ‎ (2)设点P是双曲线上任一点，该点到两渐近线的距离分别为m、n.证明是定值.‎ ‎20. （本小题满分12分）‎ 直线的右支交于不同的两点A、B.‎ ‎（I）求实数k的取值范围；‎ ‎（II）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若存在，‎ ‎　　求出k的值；若不存在，说明理由.‎ ‎2１. （本小题满分12分）‎ 已知椭圆的右焦点为，为椭圆的上顶点，为坐标原点，且△是等腰直角三角形．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）过点分别作直线，交椭圆于，两点，设两直线的斜率分别为，，且，证明：直线过定点．‎ ‎22. （本小题满分12分）‎ 已知椭圆：的离心率为，右焦点为(，0)．‎ ‎ (1) 求椭圆的方程； ‎ ‎ (2) 若过原点作两条互相垂直的射线，与椭圆交于，两点，求证：点到直线的距离为定值；‎ ‎ (3) 在（2）的条件下，求面积的最大值．‎ 高二数学（理科）试卷答案 一.选择题（每小题5分，共60分）‎ ‎1-6 ｃDcDCｃ 7-12 ｃCDBａD　‎ 二．填空题（每小题5分，共20分）‎ ‎13. 10＋2 14. 15. －2　　 16. b2‎ 三．解答题（共70分）‎ ‎17. p:0b>0)‎ ‎∵e＝，即＝，∴a＝2c 又b2＝a2－c2＝3c2‎ ‎∴椭圆方程为＋＝1.又∵椭圆过点A(2,3)‎ ‎∴＋＝1，解得c2＝4，∴椭圆方程为＋＝1.‎ 法三：∵A(2,3)，F1(－2,0)，F2(2,0)，‎ ‎∴＝(－4，－3)，＝(0，－3)，‎ ‎∴＋＝(－4，－3)＋(0，－3)‎ ‎＝－(1,2)，‎ ‎∴kl＝2，∴l：y－3＝2(x－2)，即2x－y－1＝0.‎ ‎19. （1）易知 双曲线的方程是. ‎ ‎（2）设P，已知渐近线的方程为：‎ 该点到一条渐近线的距离为：‎ 到另一条渐近线的距离为 是定值.‎ ‎２０.解：（Ⅰ）将直线 ‎……①‎ 依题意，直线l与双曲线C的右支交于不同两点，故 ‎（Ⅱ）设A、B两点的坐标分别为、，则由①式得 ‎……②‎ 假设存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F（c,0）.‎ 则由FA⊥FB得：‎ 整理得 ‎……③‎ 把②式及代入③式化简得 解得 可知使得以线段AB为直径的圆经过双曲线C的右焦点.‎ ‎2１．解：（1）由△是等腰直角三角形，得c2＝2＝4, a2＝8 ‎ 故椭圆方程为 　……4分　　　 ‎ ‎（2）①若直线的斜率存在，设方程为，依题意．‎ 设，，‎ 由 得 ． ……6分 则． ……7分 由已知，可得，‎ 所以 即。‎ 所以，整理得…………9分 故直线AB的方程为 所以直线AB过定点…………10分 若直线AB的斜率不存在，设AB方程为，设 由已知，得，此时AB方程为，显然过点。‎ 综上所述，直线AB过定点…………12分 ‎ ‎22. 解：（1） ……… 3分 ‎ （2） 设，，若k存在，则设直线AB：y＝kx＋m.‎ ‎ 由，得……………5分 △ ‎＞0， …………6分 有OA⊥OB知x1x2＋y1y2＝x1x2＋(k x1＋m) (k x2＋m)‎ ‎ ＝(1＋k2) x1x2＋k m(x1＋x2)＝0 ……8分 ‎ ‎ 代入，得4 m2＝3 k2＋3‎ 原点到直线AB的距离d＝. ………………9分 ‎ ‎ 当AB的斜率不存在时，,可得，依然成立． ‎ ‎ 所以点O到直线的距离为定值 ……………10分 说明：直接设直线OA的斜率为K相应给分 ‎（3） ‎ ‎＝ ＝≤4 ………12分 当且仅当，即时等号成立. ………………13分 当斜率不存在时，经检验|AB|＜2.所以≤ ‎