2017-2018学年陕西省黄陵中学高二（重点班）上学期期末考试数学试题 Word版

2017-2018学年陕西省黄陵中学高二（重点班）上学期期末考试数学试题 Word版

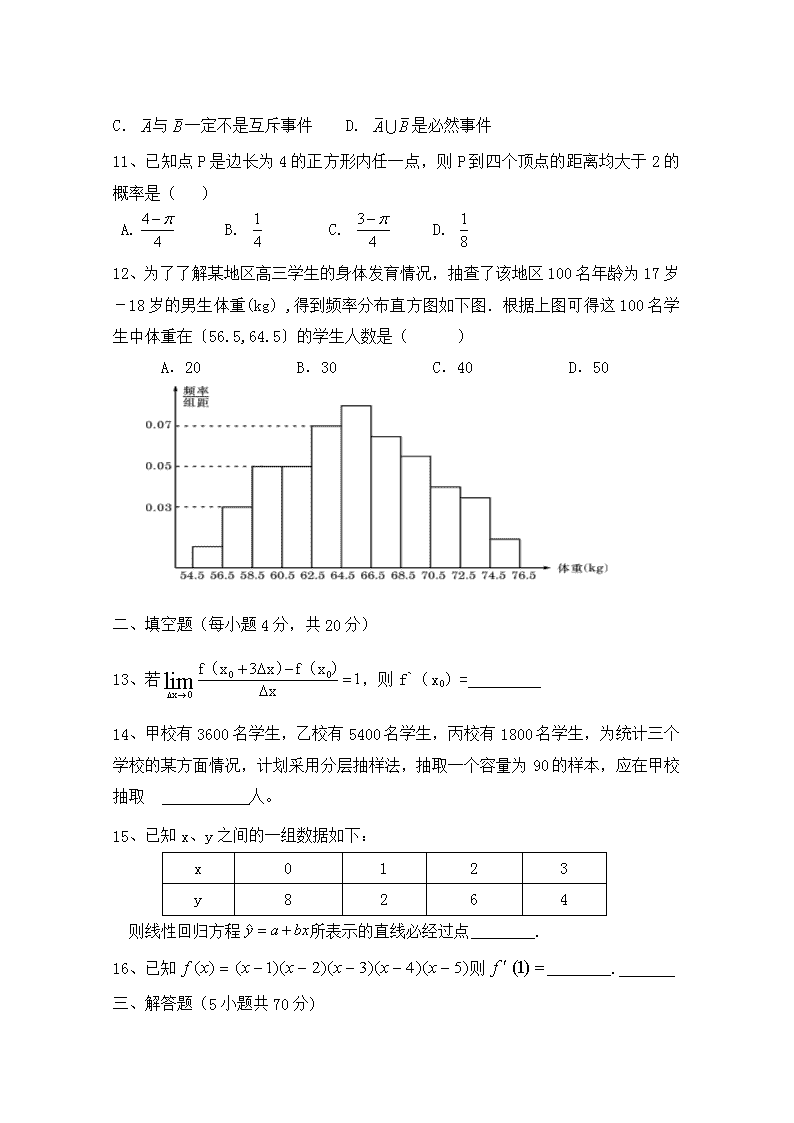
‎2017-2018学年陕西省黄陵中学高二（重点班）上学期期末考试数学试题 一、选择题（每小题5分，12小题共60分）： ‎ ‎1．有一个几何体的三视图如下图所示，这个几何体应是一个（ ）‎ A．棱台 B．棱锥 C．棱柱 D．都不对 ‎2、算法的三种基本结构是 ( )‎ ‎ A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构 ‎ C.顺序结构、条件结构、循环结构 D. 模块结构、条件结构、循环结构 ‎3、将两个数a=8, b=17交换,使a=17,b=8,下面语句正确一组是 ( )‎ b=a a=b c=b b=a a=c a=c c=b b=a a=b b=a ‎ ‎ ‎ ‎ ‎ （A） （ B ） （ C） （ D）‎ ‎4、一个年级有16个班级，每个班级学生从1到50号编排，为了交流学习经验，要求每班编号为14的同学留下进行交流，这里运用的是 （ ）‎ A．分层抽样 B．抽签法 C．系统抽样 D．随机数表法 ‎5.异面直线是指（　　） ‎ Ａ．空间中两条不相交的直线 ‎ Ｂ．分别位于两个不同平面内的两条直线 Ｃ．平面内的一条直线与平面外的一条直线 ‎ Ｄ．不同在任何一个平面内的两条直线 ‎ ‎6.如图所示，在正四棱柱中，‎ 则以下结论中不成立的是　（　　） （第8题图） ‎ Ａ．与Ｂ．‎ Ｃ．　Ｄ．‎ ‎7、某几何体的三视图如图所示，则该几何体的表 面积为(      )‎ A. ‎  B.＋6 ‎ C.＋5  D.＋5‎ 8、 读程序　‎ ‎ 甲：INPUT i＝1 乙：INPUT i＝1000‎ ‎ S＝0 S＝0‎ ‎ WHILE i＜＝1000 DO ‎ S＝S＋i S＝S＋i ‎ i＝i＋l i＝i一1‎ ‎ WEND LOOP UNTIL i＜1‎ ‎ PRINT S PRINT S ‎ END END 对甲乙两程序和输出结果判断正确的是（ ）‎ A．程序不同，结果不同 B．程序不同，结果相同　‎ C．程序相同，结果不同 D．程序相同，结果相同 ‎9、某篮球运动员在一个赛季的40场比赛中 的得分的茎叶图如右下图所示：‎ 则中位数与众数分别为 （ ）‎ A．3与3 B．23与23 ‎ ‎ C．3与23 D．23与3‎ ‎10、如果事件A与B是互斥事件，则（ ） ‎ A．是必然事件 B．与一定是互斥事件 ‎ C．与一定不是互斥事件 D．是必然事件 ‎11、已知点P是边长为4的正方形内任一点，则P到四个顶点的距离均大于2的概率是（ ）‎ ‎ A. B. C. D. ‎ ‎12、为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17岁－18岁的男生体重(kg) ,得到频率分布直方图如下图．根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是（ ） ‎ ‎ A．20 B．30 C．40 D．50‎ 二、填空题（每小题4分，共20分）‎ ‎13、若，则f`（x0）= 　‎ ‎14、甲校有3600名学生，乙校有5400名学生，丙校有1800名学生，为统计三个学校的某方面情况，计划采用分层抽样法，抽取一个容量为90的样本，应在甲校抽取  人。‎ ‎15、已知x、y之间的一组数据如下：‎ x ‎0‎ ‎1‎ ‎2‎ ‎3‎ y ‎8‎ ‎2‎ ‎6‎ ‎4‎ 则线性回归方程所表示的直线必经过点________.‎ ‎16、已知则________. ‎ 三、解答题（5小题共70分) ‎ ‎17、(本小题满分10分)‎ 从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试．现这两名学生在相同条件下各射箭10次，命中的环数如下：‎ 甲 ‎8‎ ‎9‎ ‎7‎ ‎9‎ ‎7‎ ‎6‎ ‎10‎ ‎10‎ ‎8‎ ‎6‎ 乙 ‎10‎ ‎9‎ ‎8‎ ‎6‎ ‎8‎ ‎7‎ ‎9‎ ‎7‎ ‎8‎ ‎8‎ ‎(1)计算甲、乙两人射箭命中环数的平均数和标准差；‎ ‎(2)比较两个人的成绩，然后决定选择哪名学生参加射箭比赛．‎ ‎18、(本小题满分15分)‎ 从含有两件正品a,b和一件次品c的3件产品中每次任取一件，连续取两次，求取出的两件产品中，恰有一件是次品的概率。‎ ‎ （1）每次取出不放回；（2）每次取出放回；‎ ‎19、(本小题满分15分)‎ 某射击运动员射击1次，命中10环、9环、8环、7环（假设命中的环数都为整数）的概率分别为0.20，0.22，0.25，0.28. 计算该运动员在1次射击中： ‎ ‎ (1)至少命中7环的概率； ‎ ‎(2)命中不足8环的概率.‎ ‎20、（本题满分15分）假设关于某设备的使用年限和所支出的维修费用(万元),有如下的统计数据由资料知对呈线性相关,并且统计的五组数据得平均值分别为,,若用五组数据得到的线性回归方程去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,‎ ‎（1）求回归直线方程;‎ （2） 估计使用年限为10年时,维修费用是多少?‎ ‎21、(本小题满分15分)设计算法流程图，要求输入自变量的值，输出函数 的值，并用复合if语句描述算法。‎ 一、选择题（每小题5分，12小题共60分）：‎ ‎1-6 ACBCDD 7-12 CBBDAC 二、填空题（每小题5分，4小题共20分）：‎ ‎15、；16、30 ；17、（1.5,5）18、24.‎ 三、解答题（5小题共70分) ‎ ‎17、解：(1)计算得＝8，＝8；s甲≈1.41，s乙≈1.10．‎ ‎(2)由(1)可知，甲、乙两名学生射箭命中环数的平均数相等，但s乙＜s甲，这表明乙的成绩比甲更稳定一些． 故选择乙参赛更合适．‎ ‎18、解：（1）每次取出一个，取后不放回地连续取两次，其一切可能的结果组成的基本事件有6个，即（a1，a2），（a1，b2），（a2，a1）， （a2，b1），（b1，a1），（b2，a2）．用A表示“取出的两件中，恰好有一件次品”这一事件，则P（A）=4/6=2/3（2）由题意知本题是一个古典概型，试验发生包含的事件是每次取出一个，取后放回地连续取两次，其一切可能的结果组成的基本事件有9个，即（a1，a1），（a1，a2），（a1，b1），（a2，a1），（a2，a2），（a2，b1），（b1，a1）（b1，a2），（b1，b1）．用B表示“取出的两种中，恰好有一件次品”这一事件，则P（B）=4/9‎ ‎19、记事件“射击1次，命中k环”为Ak(，且)，则事件Ak彼此互斥. (1)记“射击1次，至少命中7环”为事件A，那么当A10，A9， A8，A7之一发生时，事件A发生. 由互斥事件的概率加法公式，得 ‎=0.20+0.22+0.25+0.28=0.95.‎ ‎(2)事件“射击1次，命中不足7环”是事件“射击1次，至少命中7环”的对立事件，即表示事件“射击1次，命中不足7环”. 根据对立事件的概率公式， 得 记事件“射击1次，命中不足8环”为B，那么与A7之一发生，B发生，而与A7是互斥事件，于是答：该运动员在1次射击中, 至少命中7环的概率为0.95；命中不足8环的概率为0.33. ‎ ‎20、解：(1)因为线性回归方程经过定点,将,代入回归方程得; 又;解得, 线性回归方程 (2)将代入线性回归方程得(万元) ∴线性回归方程;使用年限为10年时,维修费用是12(万元).‎ ‎21、输入；‎ if x < 0， ‎ then f(x):= π/2∙x+3；‎ else if x = 0， ‎ then f(x):=0；‎ else f(x):= π/2∙x-5. ‎ ‎ 输出f(x).‎