- 2021-06-19 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河南省洛阳市2019-2020学年八年级下学期期末考试数学试题
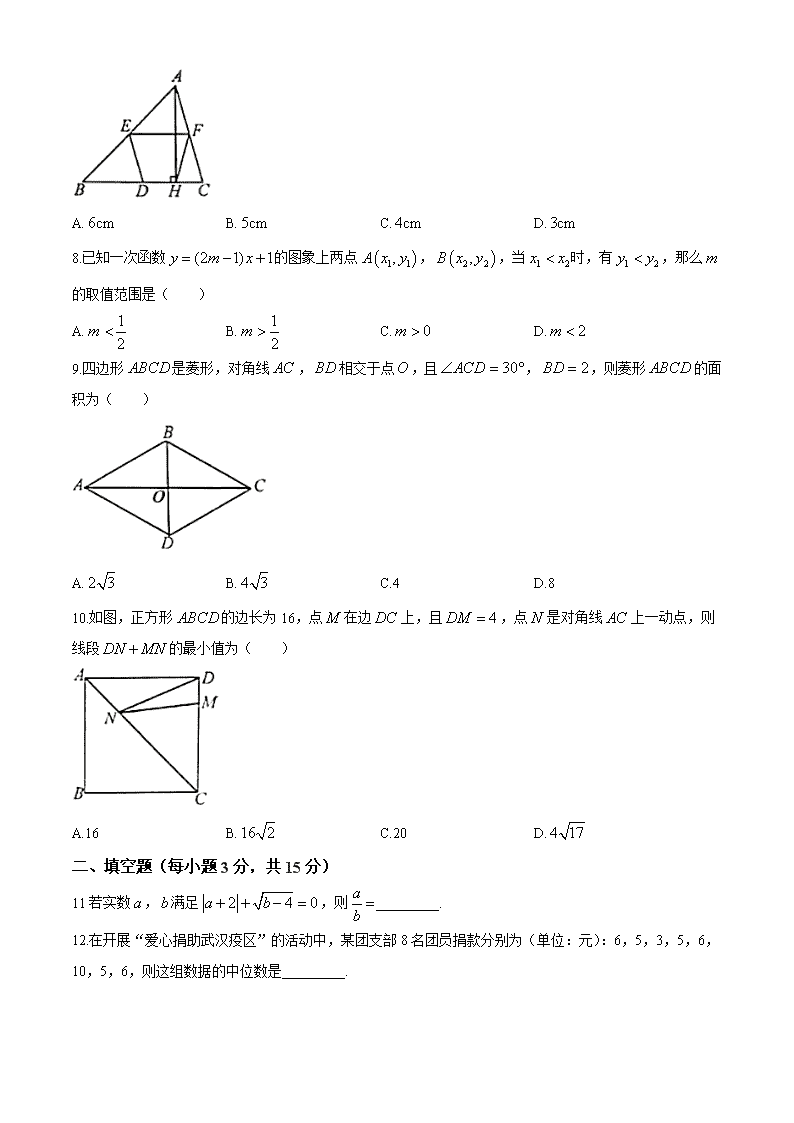
洛阳市2019—2020学年第二学期期末考试 八年级数学试卷 一、选择题(每小题3分,共30分) 1.若式子在实数范围内有意义,则的取值范围是( ) A. B. C. D. 2.下列计算:①;②;③;④ 其中正确的有( )个 A.1 B.2 C.3 D.4 3.某特警部队为了选拔“神枪手”,举行了射击比赛,最后由甲、乙两名战士进人决赛,在相同条件下,两人各射靶10次,经过统计计算,甲、乙两名战土的总成绩都是99环,甲的方差是0.28,乙的方差是0.21,则下列说法中,正确的是( ) A.甲的成绩比乙的成绩稳定 B.甲、乙两人成绩的稳定性相同 C.乙的成绩比甲的成绩稳定 D.无法确定谁的成绩更稳定 4.如图,正方形中,延长至,使,连接,则( ) A.10° B.20° C.30° D.22.5° 5.为了解某小区家庭垃圾袋的使用情况,小亮随机调查了该小区10户家庭一周垃圾袋的使用数量,结果如下(单位:个)7,9,11,8,7,14,10,8,9,7,则这组数据的众数和平均数分别是( ) A.8和9 B.7和9 C.9和7 D.7和8.5 6.面试时,某人的基本知识、表达能力、决策能力的得分分别是90分,80分,85分,若依次按20%,40%,40%的比例确定成绩,则这个人的面试成绩是( )分 A.81 B.82 C.83 D.84 7.如图,,,分别是各边的中点,是高,如果,那么的长为( ) A. B. C. D. 8.已知一次函数的图象上两点,,当时,有,那么的取值范围是( ) A. B. C. D. 9.四边形是菱形,对角线,相交于点,且,,则菱形的面积为( ) A. B. C.4 D.8 10.如图,正方形的边长为16,点在边上,且,点是对角线上一动点,则线段的最小值为( ) A.16 B. C.20 D. 二、填空题(每小题3分,共15分) 11若实数,满足,则_________. 12.在开展“爱心捐助武汉疫区”的活动中,某团支部8名团员捐款分别为(单位:元):6,5,3,5,6,10,5,6,则这组数据的中位数是_________. 13.如图,则方程组的解为_________. 14.如图,在平行四边形中,用直尺和圆规作的平分线交于点,若,,则的长为_________. 15.如图,在矩形中,,,点为边上一个动点(不与,重合),把沿折叠,当点的对应点落在矩形的对称轴上时,的长为_________. 三、解答題(共75分) 16.计算 (1) (2) 17.如图,某学校(点)到公路(直线)的距离为,到公交站(点)的距离为,现在公路边上建一个商店(点),使商店到学校及公交站的距离相等,求商店与公交站之间的距离(结果保留整数). 18.某校为迎接中华人民共和国建国70周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如图所示: 根据以上信息,解答下列问题: (1)补全上面两幅统计图;填出本次所抽取学生四月份“读书量”的中位数为_________; (2)求本次所抽取学生四月份“读书量”的平均数; (3)已知该校七年级有600名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数. 19.如图,已知一次函数与的图象交于点, (1)求的值; (2)若点是直线上的点且,求点的坐标; (3)直接写出时,的取值范围. 20.如图,点、、、在同一直线上,点和点分别在直线的两侧,且,,. (1)求证:四边形是平行四边形; (2)若,,,当为_________时,四边形是菱形. 21.某营业厅销售3部型号手机和2部型号手机的营业额为10800元,销售4部型号手机和1部型号手机的营业额为10400元. (1)求每部型号手机和型号手机的售价; (2)该营业厅计划一次性购进两种型号手机共50部,其中型号手机的进货数量不超过型号手机数量的2倍.已知型手机和型手机的进货价格分别为1500元/部和1800元/部,设购进型号手机部,这50部手机的销售总利润为元. ①求关于的函数关系式; ②该营业厅购进型号和型号手机各多少部时,才能使销售总利润最大,最大利润为多少元? 22.已知,在中,,,为直线上一动点(不与点,重合),以为边作正方形,连接. (1)如图1,当点在线段上时,与的位置关系是_________,、、三条线段之间的数量关系为_________; (2)如图2,当点在线段的延长线上时,其他条件不变,请猜想与的位置关系及,,三条线段之间的数量关系并证明; (3)如图3,当点在线段的反向延长线上时,点,分别在直线的两侧,其他条件不变,若正方形的对角线,相交于点,,,则的面积为_________(直接写出答案). 23.如图,一次函数与轴交于点,一次函数与轴交于点,且它们的图像都经过点. (1)则点的坐标为_________,点的坐标为_________; (2)在轴上有一点,且,如果和的面积相等,求的值; (3)在(2)的条件下,在轴的右侧,以为腰作等腰直角,直接写出满足条件的点的坐标. 洛阳市2019—2020学年第二学期期末考试 八年级数学试卷参考答案 一、选择题 1.C2.B3.C4.D5.B6.D7.A8.B9.A10.C 二、填空题 11. 12.5.5 13. 14. 15.或 三、解答题 16.解:(1)原式 (2)原式 17.解:作于,则, ∴ 设,则 , 在中 解得 答:商店与车站之间的距离约为. 18.解:(1)画图略,补充条形高度12,补充扇形百分数为35%, 中位数为3本 (2)平均数 (3)(人) 答:四月份“读书量”为5本的学生人数约为60人. 19.解:(1)∵交点在直线上 ∴解得 (2)设 作轴,轴交于,则是 等腰直角三角形,且 则 ∴ ∴∴或0 ∴或 (3)当时,的取值范围为: 20.证明:(1)连接交于点,连接、 ∵ ∴ ∵ ∴四边形是平行四边形 ∴, ∵ ∴ ∴四边形是平行四边形 (其它证法可酌情给分) (2)2.8 21.解:(1)设每部型号手机的售价为元,每部型号手机的售价为元. 由题意,得,解得 答:每部型号手机的售价为2000元,每部型号手机的售价为2400元 (2)①由题意,得 ∴关于的函数关系式为 ②又,解得 ∵为正整数,∴ ∵,∴当时,销售总利润最大, 最大利润. 此时(部) 答:该营业厅购进型号手机17部,型号手机33部时,销售总利润最大, 最大利润为28300元. 22.(1)垂直 (2); 证明如下: ∵在中,, ∴ ∴ ∵在正方形中, , ∴ 即 ∴ ∴ ∴ ∴ (3) 23.(1), (2)设直线交轴于点,则 ∵且 ∴ ∵ 且 ∴ ∴ (3)查看更多