2020年山东省聊城市中考数学试卷【word版本；可编辑；含答案】

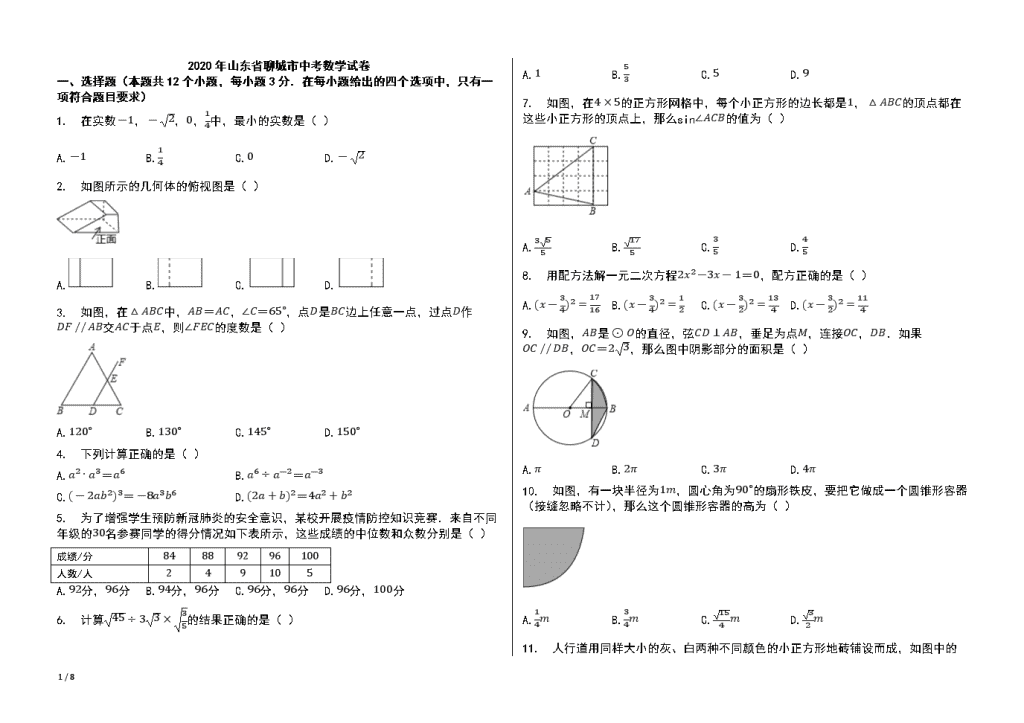
2020年山东省聊城市中考数学试卷【word版本；可编辑；含答案】

‎2020年山东省聊城市中考数学试卷 一、选择题（本题共12个小题，每小题3分．在每小题给出的四个选项中，只有一项符合题目要求）‎ ‎1. 在实数‎-1‎，‎-‎‎2‎，‎0‎，‎1‎‎4‎中，最小的实数是（ ）‎ A.‎-1‎ B.‎1‎‎4‎ C.‎0‎ D.‎‎-‎‎2‎ ‎2. 如图所示的几何体的俯视图是（ ）‎ A. B. C. D.‎ ‎3. 如图，在‎△ABC中，AB＝AC，‎∠C＝‎65‎‎∘‎，点D是BC边上任意一点，过点D作DF // AB交AC于点E，则‎∠FEC的度数是（ ）‎ A.‎120‎‎∘‎ B.‎130‎‎∘‎ C.‎145‎‎∘‎ D.‎‎150‎‎∘‎ ‎4. 下列计算正确的是（ ）‎ A.a‎2‎‎⋅‎a‎3‎＝a‎6‎ B.a‎6‎‎÷‎a‎-2‎＝‎a‎-3‎ C.‎(-2ab‎2‎‎)‎‎3‎＝‎-8‎a‎3‎b‎6‎ D.‎(2a+b‎)‎‎2‎＝‎‎4a‎2‎+‎b‎2‎ ‎5. 为了增强学生预防新冠肺炎的安全意识，某校开展疫情防控知识竞赛．来自不同年级的‎30‎名参赛同学的得分情况如下表所示，这些成绩的中位数和众数分别是（ ）‎ 成绩/分 ‎84‎ ‎88‎ ‎92‎ ‎96‎ ‎100‎ 人数/人 ‎2‎ ‎4‎ ‎9‎ ‎10‎ ‎5‎ A.‎92‎分，‎96‎分 B.‎94‎分，‎96‎分 C.‎96‎分，‎96‎分 D.‎96‎分，‎100‎分 ‎6. 计算‎45‎‎÷3‎3‎×‎‎3‎‎5‎的结果正确的是（ ）‎ A.‎1‎ B.‎5‎‎3‎ C.‎5‎ D.‎‎9‎ ‎7. 如图，在‎4×5‎的正方形网格中，每个小正方形的边长都是‎1‎，‎△ABC的顶点都在这些小正方形的顶点上，那么sin∠ACB的值为（ ）‎ A.‎3‎‎5‎‎5‎ B.‎17‎‎5‎ C.‎3‎‎5‎ D.‎‎4‎‎5‎ ‎8. 用配方法解一元二次方程‎2x‎2‎-3x-1‎＝‎0‎，配方正确的是（ ）‎ A.‎(x-‎3‎‎4‎‎)‎‎2‎=‎‎17‎‎16‎ B.‎(x-‎3‎‎4‎‎)‎‎2‎=‎‎1‎‎2‎ C.‎(x-‎3‎‎2‎‎)‎‎2‎=‎‎13‎‎4‎ D.‎‎(x-‎3‎‎2‎‎)‎‎2‎=‎‎11‎‎4‎ ‎9. 如图，AB是‎⊙O的直径，弦CD⊥AB，垂足为点M，连接OC，DB．如果OC // DB，OC＝‎2‎‎3‎，那么图中阴影部分的面积是（ ）‎ A.π B.‎2π C.‎3π D.‎‎4π ‎10. 如图，有一块半径为‎1m，圆心角为‎90‎‎∘‎的扇形铁皮，要把它做成一个圆锥形容器（接缝忽略不计），那么这个圆锥形容器的高为（ ）‎ A.‎1‎‎4‎m B.‎3‎‎4‎m C.‎15‎‎4‎m D.‎‎3‎‎2‎m ‎11. ‎ ‎ 8 / 8‎ ‎ 人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成，如图中的每一个小正方形表示一块地砖．如果按图①②③…的次序铺设地砖，把第n个图形用图ⓝ表示，那么图㊿中的白色小正方形地砖的块数是（ ）‎ A.‎150‎ B.‎200‎ C.‎355‎ D.‎‎505‎ ‎12. 如图，在Rt△ABC中，AB＝‎2‎，‎∠C＝‎30‎‎∘‎，将Rt△ABC绕点A旋转得到Rt△AB'C'‎，使点B的对应点B'‎落在AC上，在B'C'‎上取点D，使B'D＝‎2‎，那么点D到BC的距离等于（ ）‎ A.‎2(‎3‎‎3‎+1)‎ B.‎3‎‎3‎‎+1‎ C.‎3‎‎-1‎ D.‎‎3‎‎+1‎ 二、填空题（本题共5个小题，每小题3分，共15分．只要求填写最后结果）‎ ‎13. 因式分解：x(x-2)-x+2‎＝________．‎ ‎14. 如图，在‎⊙O中，四边形OABC为菱形，点D在AmC上，则‎∠ADC的度数是________．‎ ‎15. 计算：‎(1+a‎1-a)÷‎1‎a‎2‎‎-a=‎________．‎ ‎16. 某校开展读书日活动，小亮和小莹分别从校图书馆的“科技”、“文学”、“艺术”三类书籍中随机地抽取一本，抽到同一类书籍的概率是________．‎ ‎17. 如图，在直角坐标系中，点A(1, 1)‎，B(3, 3)‎是第一象限角平分线上的两点，点C的纵坐标为‎1‎，且CA＝CB，在y轴上取一点D，连接AC，BC，AD，BD，使得四边形ACBD的周长最小，这个最小周长的值为________．‎ 三、解答题（本题共8个小题，共69分．解答题应写出文字说明、证明过程或推演步骤）‎ ‎18. 解不等式组‎1‎‎2‎x+1<7-‎3‎‎2‎x,‎‎3x-2‎‎3‎‎≥x‎3‎+x-4‎‎4‎,‎‎ ‎并写出它的所有整数解．‎ ‎19. 为了提高学生的综合素养，某校开设了五门手工活动课，按照类别分为：A“剪纸”、B“沙画”、C“葫芦雕刻”、D“泥塑”、E“插花”．为了了解学生对每种活动课的喜爱情况，随机抽取了部分同学进行调查，将调查结果绘制成如图两幅不完整的统计图．‎ ‎ 8 / 8‎ 根据以上信息，回答下列问题： ‎ ‎（1）本次调查的样本容量为________；统计图中的a＝________，b＝________；‎ ‎（2）通过计算补全条形统计图；‎ ‎（3）该校共有‎2500‎名学生，请你估计全校喜爱“葫芦雕刻”的学生人数．‎ ‎20. 今年植树节期间，某景观园林公司购进一批成捆的A，B两种树苗，每捆A种树苗比每捆B种树苗多‎10‎棵，每捆A种树苗和每捆B种树苗的价格分别是‎630‎元和‎600‎元，而每棵A种树苗和每棵B种树苗的价格分别是这一批树苗平均每棵价格的‎0.9‎倍和‎1.2‎倍． ‎ ‎（1）求这一批树苗平均每棵的价格是多少元？‎ ‎（2）如果购进的这批树苗共‎5500‎棵，A种树苗至多购进‎3500‎棵，为了使购进的这批树苗的费用最低，应购进A种树苗和B种树苗各多少棵？并求出最低费用．‎ ‎21. 如图，在‎▱ABCD中，E为BC的中点，连接AE并延长交DC的延长线于点F，连接BF，AC，若AD＝AF，求证：四边形ABFC是矩形．‎ ‎22. 如图，小莹在数学综合实践活动中，利用所学的数学知识对某小区居民楼AB ‎ 8 / 8‎ 的高度进行测量，先测得居民楼AB与CD之间的距离AC为‎35m，后站在M点处测得居民楼CD的顶端D的仰角为‎45‎‎∘‎，居民楼AB的顶端B的仰角为‎55‎‎∘‎，已知居民楼CD的高度为‎16.6m，小莹的观测点N距地面‎1.6m．求居民楼AB的高度（精确到lm）．（参考数据：sin‎55‎‎∘‎≈0.82‎，cos‎55‎‎∘‎≈0.57‎，tan‎55‎‎∘‎≈l.43‎）．‎ ‎23. 如图，已知反比例函数y=‎kx的图象与直线y＝ax+b相交于点A(-2, 3)‎，B(1, m)‎．‎ ‎ ‎ ‎（1）求出直线y＝ax+b的表达式；‎ ‎（2）在x轴上有一点P使得‎△PAB的面积为‎18‎，求出点P的坐标．‎ ‎24. 如图，在‎△ABC中，AB＝BC，以‎△ABC的边AB为直径作‎⊙O，交AC于点D，过点D作DE⊥BC，垂足为点E．‎ ‎ 8 / 8‎ ‎ ‎ ‎（1）试证明DE是‎⊙O的切线；‎ ‎（2）若‎⊙O的半径为‎5‎，AC＝‎6‎‎10‎，求此时DE的长．‎ ‎25. 如图，二次函数y=ax‎2‎+bx+4‎的图象与x轴交于点A(-1, 0)‎，B(4, 0)‎，与y轴交于点C，抛物线的顶点为D，其对称轴与线段BC交于点E，垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F，动直线l在抛物线的对称轴的右侧（不含对称轴）沿x轴正方向移动到B点．‎ ‎ ‎ ‎（1）求出二次函数y＝ax‎2‎+bx+4‎和BC所在直线的表达式；‎ ‎（2）在动直线l移动的过程中，试求使四边形DEFP为平行四边形的点P的坐标；‎ ‎（3）连接CP，CD，在动直线l移动的过程中，抛物线上是否存在点P，使得以点P，C，F为顶点的三角形与‎△DCE相似？如果存在，求出点P的坐标；如果不存在，请说明理由．‎ ‎ 8 / 8‎ 参考答案与试题解析 ‎2020年山东省聊城市中考数学试卷 一、选择题（本题共12个小题，每小题3分．在每小题给出的四个选项中，只有一项符合题目要求）‎ ‎1.D ‎2.C ‎3.B ‎4.C ‎5.B ‎6.A ‎7.D ‎8.A ‎9.B ‎10.C ‎11.C ‎12.D 二、填空题（本题共5个小题，每小题3分，共15分．只要求填写最后结果）‎ ‎13.‎‎(x-2)(x-1)‎ ‎14.‎‎60‎‎∘‎ ‎15.‎‎-a ‎16.‎‎1‎‎3‎ ‎17.‎‎4+2‎‎5‎ 三、解答题（本题共8个小题，共69分．解答题应写出文字说明、证明过程或推演步骤）‎ ‎18.‎1‎‎2‎x+1<7-‎3‎‎2‎x‎3x-2‎‎3‎‎≥x‎3‎+‎x-4‎‎4‎‎ ‎，‎ 解不等式①，x<3‎，‎ 解不等式②，得x≥-‎‎4‎‎5‎，‎ ‎∴ 原不等式组的解集为‎-‎4‎‎5‎≤x<3‎，‎ 它的所有整数解为‎0‎，‎1‎，‎2‎．‎ ‎19.‎120‎,‎12‎,‎‎36‎ 该校‎2500‎名学生中喜爱“葫芦雕刻”的有‎625‎人 ‎20.这一批树苗平均每棵的价格是‎20‎元；‎ 购进A种树苗‎3500‎棵，BA种树苗‎2000‎棵时，能使得购进这批树苗的费用最低，最低费用为‎111000‎元 ‎21.证明：∵ 四边形ABCD是平行四边形，‎ ‎∴ AB // CD，AB＝CD，‎ ‎∴ ‎∠BAE＝‎∠CFE，‎∠ABE＝‎∠FCE，‎ ‎∵ E为BC的中点，‎ ‎∴ EB＝EC，‎ ‎∴ ‎△ABE≅△FCE(AAS)‎，‎ ‎∴ AB＝CF．‎ ‎∵ AB // CF，‎ ‎∴ 四边形ABFC是平行四边形，‎ ‎∵ BC＝AF，‎ ‎∴ 四边形ABFC是矩形．‎ ‎22.居民楼AB的高度约为‎30‎米 ‎23.将点A的坐标代入反比例函数表达式并解得：k＝‎-2×3‎＝‎-6‎，‎ 故反比例函数表达式为：y=-‎‎6‎x，‎ 将点B的坐标代入上式并解得：m＝‎-6‎，故点B(1, -6)‎，‎ 将点A、B的坐标代入一次函数表达式得‎3=-2a+b‎-6=a+b‎ ‎，解得a=-3‎b=-3‎‎ ‎，‎ 故直线的表达式为：y＝‎-3x-3‎；‎ 设直线与x轴的交点为E，当y＝‎0‎时，x＝‎-1‎，故点E(-1, 0)‎，‎ 分别过点A、B作x轴的垂线AC、BD，垂足分别为C、D，‎ ‎ 8 / 8‎ 则S‎△PAB‎=‎1‎‎2‎PE⋅CA+‎1‎‎2‎PE⋅BD=‎3‎‎2‎PE+‎6‎‎2‎PE=‎9‎‎2‎PE＝‎18‎，解得：PE＝‎4‎，‎ 故点P的坐标为‎(3, 0)‎或‎(-5, 0)‎．‎ ‎24.证明：连接OD、BD，‎ ‎∵ AB是‎⊙O直径，‎ ‎∴ ‎∠ADB＝‎90‎‎∘‎，‎ ‎∴ BD⊥AC，‎ ‎∵ AB＝BC，‎ ‎∴ D为AC中点，‎ ‎∵ OA＝OB，‎ ‎∴ OD // BC，‎ ‎∵ DE⊥BC，‎ ‎∴ DE⊥OD，‎ ‎∵ OD为半径，‎ ‎∴ DE是‎⊙O的切线；‎ 由（1）知BD是AC的中线，‎ ‎∴ AD＝CD=‎1‎‎2‎AC=3‎‎10‎，‎ ‎∵ O的半径为‎5‎，‎ ‎∴ AB＝‎6‎，‎ ‎∴ BD=AB‎2‎-AD‎2‎=‎10‎‎2‎‎-(3‎‎10‎‎)‎‎2‎=‎‎10‎，‎ ‎∵ AB＝AC，‎ ‎∴ ‎∠A＝‎∠C，‎ ‎∵ ‎∠ADB＝‎∠CED＝‎90‎‎∘‎，‎ ‎∴ ‎△CDE∽△ABD，‎ ‎∴ CDAB‎=‎DEBD，即‎3‎‎10‎‎10‎‎=‎DE‎10‎，‎ ‎∴ DE＝‎3‎．‎ ‎25.将点A(-1, 0)‎，B(4, 0)‎，代入y=ax‎2‎+bx+4‎，‎ 得：‎0=a-b+4‎‎0=16a+4b+4‎‎ ‎，‎ 解得：a=-1‎b=3‎‎ ‎，‎ ‎∴ 二次函数的表达式为：y＝‎-x‎2‎+3x+4‎，‎ 当x＝‎0‎时，y＝‎4‎，‎ ‎∴ C(0, 4)‎，‎ 设BC所在直线的表达式为：y＝mx+n，‎ 将C(0, 4)‎、B(4, 0)‎代入y＝mx+n，‎ 得：‎4=n‎0=4m+n‎ ‎，‎ 解得：m=-1‎n=4‎‎ ‎，‎ ‎∴ BC所在直线的表达式为：y＝‎-x+4‎；‎ ‎∵ DE⊥x轴，PF⊥x轴，‎ ‎∴ DE // PF，‎ 只要DE＝PF，四边形DEFP即为平行四边形，‎ ‎∵ y＝‎-x‎2‎+3x+4‎＝‎-(x-‎3‎‎2‎‎)‎‎2‎+‎‎25‎‎4‎，‎ ‎∴ 点D的坐标为：‎(‎3‎‎2‎, ‎25‎‎4‎)‎，‎ 将x=‎‎3‎‎2‎代入y＝‎-x+4‎，即y=-‎3‎‎2‎+4=‎‎5‎‎2‎，‎ ‎ 8 / 8‎ ‎∴ 点E的坐标为：‎(‎3‎‎2‎, ‎5‎‎2‎)‎，‎ ‎∴ DE=‎25‎‎4‎-‎5‎‎2‎=‎‎15‎‎4‎，‎ 设点P的横坐标为t，‎ 则P的坐标为：‎(t, -t‎2‎+3t+4)‎，F的坐标为：‎(t, -t+4)‎，‎ ‎∴ PF＝‎-t‎2‎+3t+4-(-t+4)‎＝‎-t‎2‎+4t，‎ 由DE＝PF得：‎-t‎2‎+4t=‎‎15‎‎4‎，‎ 解得：t‎1‎‎=‎‎3‎‎2‎（不合题意舍去），t‎2‎‎=‎‎5‎‎2‎，‎ 当t=‎‎5‎‎2‎时，‎-t‎2‎+3t+4‎＝‎-(‎5‎‎2‎‎)‎‎2‎+3×‎5‎‎2‎+4=‎‎21‎‎4‎，‎ ‎∴ 点P的坐标为‎(‎5‎‎2‎, ‎21‎‎4‎)‎；‎ 存在，理由如下：‎ 如图‎2‎所示：‎ 由（2）得：PF // DE，‎ ‎∴ ‎∠CED＝‎∠CFP，‎ 又∵ ‎∠PCF与‎∠DCE有共同的顶点C，且‎∠PCF在‎∠DCE的内部，‎ ‎∴ ‎∠PCF≠∠DCE，‎ ‎∴ 只有‎∠PCF＝‎∠CDE时，‎△PCF∽△CDE，‎ ‎∴ PFCE‎=‎CFDE，‎ ‎∵ C(0, 4)‎、E(‎3‎‎2‎, ‎5‎‎2‎)‎，‎ ‎∴ CE=‎(‎3‎‎2‎‎)‎‎2‎+(4-‎‎5‎‎2‎‎)‎‎2‎=‎‎3‎‎2‎‎2‎，‎ 由（2）得：DE=‎‎15‎‎4‎，PF＝‎-t‎2‎+4t，F的坐标为：‎(t, -t+4)‎，‎ ‎∴ CF=t‎2‎‎+[4-(-t+4)‎‎]‎‎2‎=‎2‎t，‎ ‎∴ ‎-t‎2‎+4t‎3‎‎2‎‎2‎‎=‎‎2‎t‎15‎‎4‎，‎ ‎∵ t≠0‎，‎ ‎∴ ‎15‎‎4‎‎(-t+4)‎＝‎3‎，‎ 解得：t=‎‎16‎‎5‎，‎ 当t=‎‎16‎‎5‎时，‎-t‎2‎+3t+4‎＝‎-(‎16‎‎5‎‎)‎‎2‎+3×‎16‎‎5‎+4=‎‎84‎‎25‎，‎ ‎∴ 点P的坐标为：‎(‎16‎‎5‎, ‎84‎‎25‎)‎．‎ ‎ 8 / 8‎