2020高中数学分段函数

2020高中数学分段函数

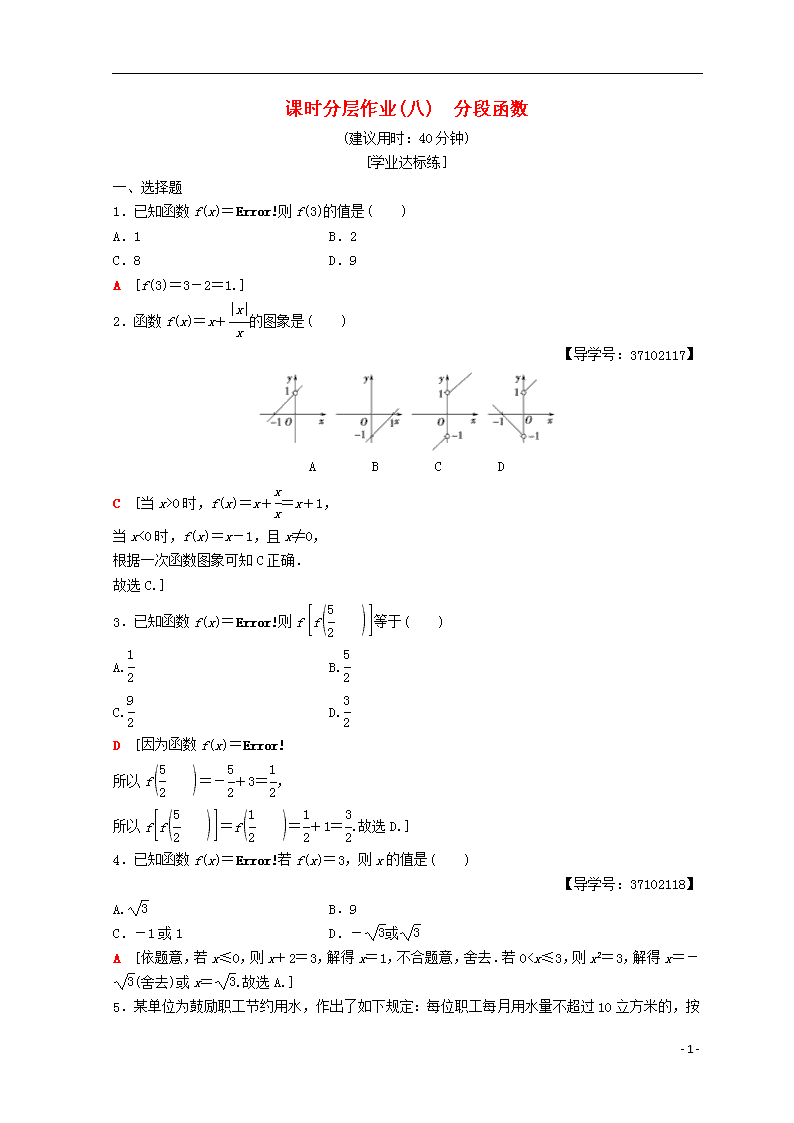
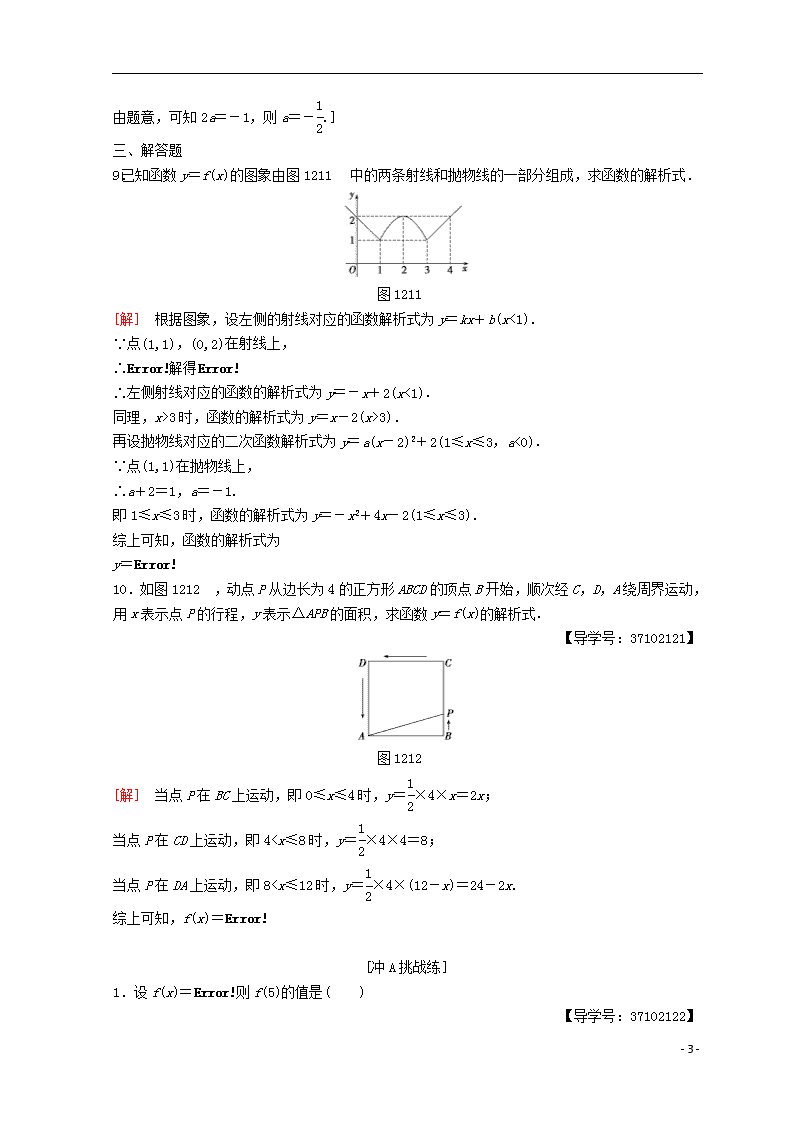
课时分层作业(八)　分段函数 ‎(建议用时：40分钟)‎ ‎[学业达标练]‎ 一、选择题 ‎1．已知函数f(x)＝则f(3)的值是(　　)‎ A．1　　　　　　　　 B．2‎ C．8 D．9‎ A　[f(3)＝3－2＝1.]‎ ‎2．函数f(x)＝x＋的图象是(　　) ‎ ‎【导学号：37102117】‎ A　　　　B　　　　C　　　　D C　[当x>0时，f(x)＝x＋＝x＋1，‎ 当x<0时，f(x)＝x－1，且x≠0，‎ 根据一次函数图象可知C正确．‎ 故选C.]‎ ‎3．已知函数f(x)＝则f等于(　　)‎ A. B. C. D. D　[因为函数f(x)＝ 所以f＝－＋3＝，‎ 所以f＝f＝＋1＝.故选D.]‎ ‎4．已知函数f(x)＝若f(x)＝3，则x的值是(　　) ‎ ‎【导学号：37102118】‎ A. B．9‎ C．－1或1 D．－或 A　[依题意，若x≤0，则x＋2＝3，解得x＝1，不合题意，舍去．若010.令2mx－‎10m＝‎16m，解得x＝13.]‎ 二、填空题 ‎6．如图129，函数f(x)的图象是曲线OAB，其中点O，A，B的坐标分别为(0,0)，(1,2)，(3,1)，则f(f(3))的值等于________. ‎ ‎【导学号：37102119】‎ 图129‎ ‎2　[由图可知f(3)＝1，f(1)＝2，∴f(f(3))＝f(1)＝2.]‎ ‎7．已知函数f(x)的图象如图1210所示，则f(x)的解析式是________．‎ 图1210‎ f(x)＝　[由题图可知，图象是由两条线段组成，‎ 当－1≤x<0时，设f(x)＝ax＋b，将(－1,0)，(0,1)代入解析式，则∴即f(x)＝x＋1.‎ 当0≤x≤1时，设f(x)＝kx，将(1，－1)代入，则k＝－1，即f(x)＝－x.‎ 综上，f(x)＝]‎ ‎8．在平面直角坐标系xOy中，若直线y＝‎2a与函数y＝|x－a|－1的图象只有一个交点，则a的值为________. ‎ ‎【导学号：37102120】‎ ‎－　[在同一平面直角坐标系内，作出函数y＝‎2a与y＝|x－a|－1的大致图象，如图所示．‎ - 5 -‎ 由题意，可知‎2a＝－1，则a＝－.]‎ 三、解答题 ‎9．已知函数y＝f(x)的图象由图1211中的两条射线和抛物线的一部分组成，求函数的解析式．‎ 图1211‎ ‎[解]　根据图象，设左侧的射线对应的函数解析式为y＝kx＋b(x<1)．‎ ‎∵点(1,1)，(0,2)在射线上，‎ ‎∴解得 ‎∴左侧射线对应的函数的解析式为y＝－x＋2(x<1)．‎ 同理，x>3时，函数的解析式为y＝x－2(x>3)．‎ 再设抛物线对应的二次函数解析式为y＝a(x－2)2＋2(1≤x≤3，a<0)．‎ ‎∵点(1,1)在抛物线上，‎ ‎∴a＋2＝1，a＝－1.‎ 即1≤x≤3时，函数的解析式为y＝－x2＋4x－2(1≤x≤3)．‎ 综上可知，函数的解析式为 y＝ ‎10．如图1212，动点P从边长为4的正方形ABCD的顶点B开始，顺次经C，D，A绕周界运动，用x表示点P的行程，y表示△APB的面积，求函数y＝f(x)的解析式. ‎ ‎【导学号：37102121】‎ 图1212‎ ‎[解]　当点P在BC上运动，即0≤x≤4时，y＝×4×x＝2x；‎ 当点P在CD上运动，即4

查看更多