数学理卷·2019届甘肃省武威市第六中学高二下学期寒假学习质量检测（2018-02）

数学理卷·2019届甘肃省武威市第六中学高二下学期寒假学习质量检测（2018-02）

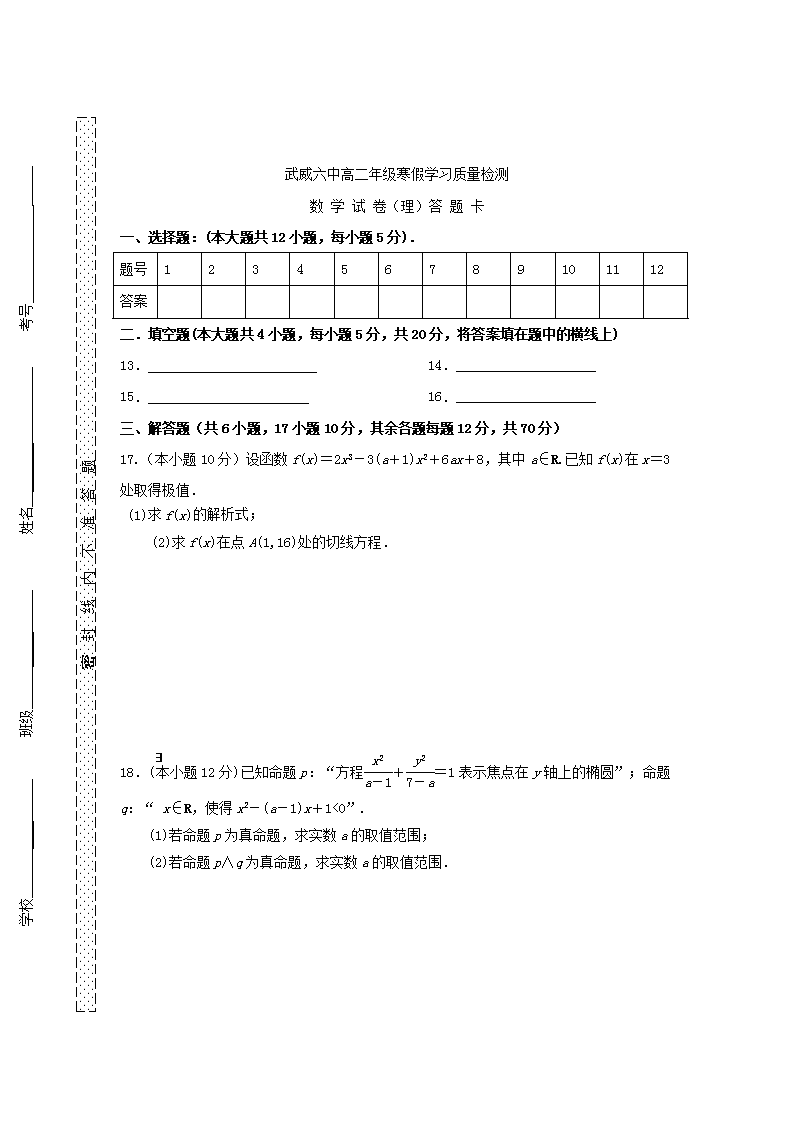
武威六中高二年级寒假学习质量检测 数 学 试 卷（理）‎ 一、选择题：(本大题共12小题，每小题5分)． ‎ ‎1．已知条件p：log2（x﹣1）＜1；条件q：|x﹣2|＜1，则p是q成立的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分又不必要条件 ‎2．设f（x）=xlnx，若，则x0等于（　　）‎ A．e2 B．e C． D．ln2‎ ‎3．如图，在空间直角坐标系中有直三棱柱ABC﹣A1B1C1，CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为（　　）‎ A． B． C． D．‎ ‎4．已知F1、F2为双曲线C：x2﹣y2=1的左、右焦点，点P在C上，∠F1PF2=60°，则|PF1|•|PF2|=（　　）‎ A．2 B．4 C．6 D．8‎ ‎5．在△ABC中，AB=2，AC=3， =，则•=（　　）‎ A．﹣ B． C．﹣ D．‎ ‎6．设p：2x2－3x＋1≤0，q：x2－(2a＋1)x＋a(a＋1)≤0，若¬p是¬q的必要不充分条件，则实数a的取值范围是 (　　)‎ A．[0，] B．(0，) ‎ C．(－∞，0]∪[，＋∞) D．(－∞，0)∪(，＋∞)‎ ‎7．将一枚质地均匀的骰子先后抛掷两次，若第一次朝上一面的点数为a，第二次朝上一面的点数为b，则函数y＝ax2－2bx＋1在(－∞，]上为减函数的概率是 (　 　)‎ A． B． C． D． ‎8．设抛物线的顶点在原点，其焦点F在y轴上，又抛物线上的点P(k，－2)与点F的距离为4，则k等于 (　　)‎ A．4 B．4或－4 C．－2 D．－2或2‎ ‎9．已知a、b是两异面直线，A、B∈a，C、D∈b，AC⊥b，BD⊥b且AB＝2，CD＝1，则直线a、b所成的角为 (　　)‎ A．30° B．60° C．90° D．45°‎ ‎10．设抛物线C：y2＝4x的焦点为F，直线l过F且与C交于A，B两点．若|AF|＝3|BF|，则l的方程为 (　　)‎ A．y＝x－1或y＝－x＋1 B．y＝(x－1)或y＝－(x－1)‎ C．y＝(x－1)或y＝－(x－1) D．y＝(x－1)或y＝－(x－1)‎ ‎11．执行两次如图所示的程序框图，若第一次输入x的值为7，‎ 第二次输入x的值为9，则第一次、第二次输出的a的值分别为 ( )‎ A．0,0 B．1,1 C．0,1 D．1,0‎ ‎12．在正四棱锥S－ABCD中，O为顶点S在底面的射影，P为侧棱SD的中点，且SO＝OD，则直线BC与平面PAC所成的角是 (　　)‎ A．75° B．60° C．45° D．30°‎ 二、填空题（共4小题，每小题5分，共计20分）‎ ‎13．函数的单调递减区间为　　　　　　．‎ ‎14．若双曲线－＝1的一个焦点与抛物线y2＝8x的焦点相同，则实数m＝________.‎ ‎15．已知在空间四边形OABC中，＝a、＝b、＝c，点M在OA上，且OM＝3MA，N为BC中点，用a、b、c表示，则等于________.‎ ‎16．边长为1的等边三角形ABC中，沿BC边高线AD折起，使得折后二面角B－AD－C为60°，点D到平面ABC的距离为________.‎ 学校 ____ 班级 _____ 姓名 _______ 考号______________ ‎ 密 封 线 内 不 准 答 题 武威六中高二年级寒假学习质量检测 数 学 试 卷（理）答 题 卡 一、选择题：(本大题共12小题，每小题5分)． ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 二．填空题(本大题共4小题，每小题5分，共20分，将答案填在题中的横线上)‎ ‎13． 14．____________________‎ ‎15． 16．____________________‎ 三、解答题（共6小题，17小题10分，其余各题每题12分，共70分）‎ ‎17.（本小题10分）设函数f(x)＝2x3－3(a＋1)x2＋6ax＋8，其中a∈R.已知f(x)在x＝3处取得极值．‎ ‎ (1)求f(x)的解析式；‎ ‎ (2)求f(x)在点A(1,16)处的切线方程．‎ ‎18．(本小题12分)已知命题p：“方程＋＝1表示焦点在y轴上的椭圆”；命题q：“∃x∈R，使得x2－(a－1)x＋1<0”.‎ ‎(1)若命题p为真命题，求实数a的取值范围；‎ ‎(2)若命题p∧q为真命题，求实数a的取值范围．‎ ‎19．(本小题满分12分)已知椭圆C的中心在坐标原点，焦点坐标为(2,0)，短轴长为4.‎ ‎(1)求椭圆C的标准方程及离心率；‎ ‎(2)设P是椭圆C上一点，且点P与椭圆C的两个焦点F1、F2构成一个直角三角形，且|PF1|>|PF2|，求的值．‎ ‎20．(本小题满分12分)已知抛物线y2＝4x截直线y＝2x＋m所得弦长|AB|＝3.‎ ‎(1)求m的值；‎ ‎(2)设P是x轴上的点，且△ABP的面积为9，求点P的坐标．‎ ‎ ‎ ‎21．如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60°．‎ ‎（Ⅰ）求证：AC⊥平面BDE； （Ⅱ）求二面角F﹣BE﹣D的余弦值；‎ ‎（Ⅲ）设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．‎ ‎22.（12分）已知函数f(x)＝x2－alnx(a∈R)．‎ ‎(1)若f(x)在x＝2时取得极值，求a的值；‎ ‎(2)求f(x)的单调区间；‎ ‎(3)求证：当x>1时，x2＋lnx0，‎ ‎∴a2－2a－3>0，∴a>3或a<－1.‎ 又∵1|PF2|，∴∠PF2F1＝90°.‎ ‎∴|PF2|＝＝＝3.‎ 又∵|PF1|＋|PF2|＝2a＝8，‎ ‎∴|PF1|＝5，∴＝.‎ ‎ 20[解析]　(1)设A(x1，y1)，B(x2，y2)，‎ 由得4x2＋4(m－1)x＋m2＝0，‎ 由根与系数的关系得x1＋x2＝1－m，x1·x2＝，‎ ‎∴|AB|＝ ‎＝ ‎＝，‎ ‎∵|AB|＝3，∴＝3，解得m＝－4.‎ ‎(2)设P(a,0)，P到直线AB的距离为d，‎ 则d＝＝，‎ 又S△ABP＝|AB|·d，则d＝，‎ ‎∴＝，∴|a－2|＝3，‎ ‎∴a＝5或a＝－1，故点P的坐标为(5,0)或(－1,0)．‎ ‎21．如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60°．‎ ‎（Ⅰ）求证：AC⊥平面BDE；‎ ‎（Ⅱ）求二面角F﹣BE﹣D的余弦值；‎ ‎（Ⅲ）设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．‎ ‎【解答】证明：（Ⅰ）因为DE⊥平面ABCD，所以DE⊥AC．‎ 因为ABCD是正方形，所以AC⊥BD，‎ 从而AC⊥平面BDE．…（4分）‎ 解：（Ⅱ）因为DA，DC，DE两两垂直，所以建立空间直角坐标系D﹣xyz如图所示．‎ 因为BE与平面ABCD所成角为600，即∠DBE=60°，‎ 所以．‎ 由AD=3，可知，．‎ 则A（3，0，0），，，B（3，3，0），C（0，3，0），‎ 所以，．‎ 设平面BEF的法向量为=（x，y，z），则，即．‎ 令，则=．‎ 因为AC⊥平面BDE，所以为平面BDE的法向量，．‎ 所以cos．‎ 因为二面角为锐角，所以二面角F﹣BE﹣D的余弦值为．…（8分）‎ ‎（Ⅲ）点M是线段BD上一个动点，设M（t，t，0）．‎ 则．‎ 因为AM∥平面BEF，‎ 所以=0，即4（t﹣3）+2t=0，解得t=2．‎ 此时，点M坐标为（2，2，0），‎ 即当时，AM∥平面BEF．…（12分）‎ ‎22.解：(1)f′(x)＝x－，因为x＝2是一个极值点，‎ 所以2－＝0.所以a＝4.‎ 此时f′(x)＝x－＝＝.‎ 因为f(x)的定义域是{x|x>0}，‎ 所以当02时，f′(x)>0.‎ 所以当a＝4时，x＝2是f(x)的极小值点．所以a＝4.‎ ‎(2)因为f′(x)＝x－，‎ 所以当a≤0时，f(x)的单调递增区间为(0，＋∞)．‎ 当a>0时，f′(x)＝x－＝＝，‎ 令f′(x)>0有x>，‎ 所以函数f(x)的单调递增区间为(，＋∞)；‎ 令f′(x)<0有01时，g′(x)＝>0，‎ 所以g(x)在(1，＋∞)上是增函数．‎ 所以g(x)>g(1)＝>0.‎ 所以当x>1时，x2＋lnx

查看更多