- 2021-06-19 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学下册 第2章圆周角
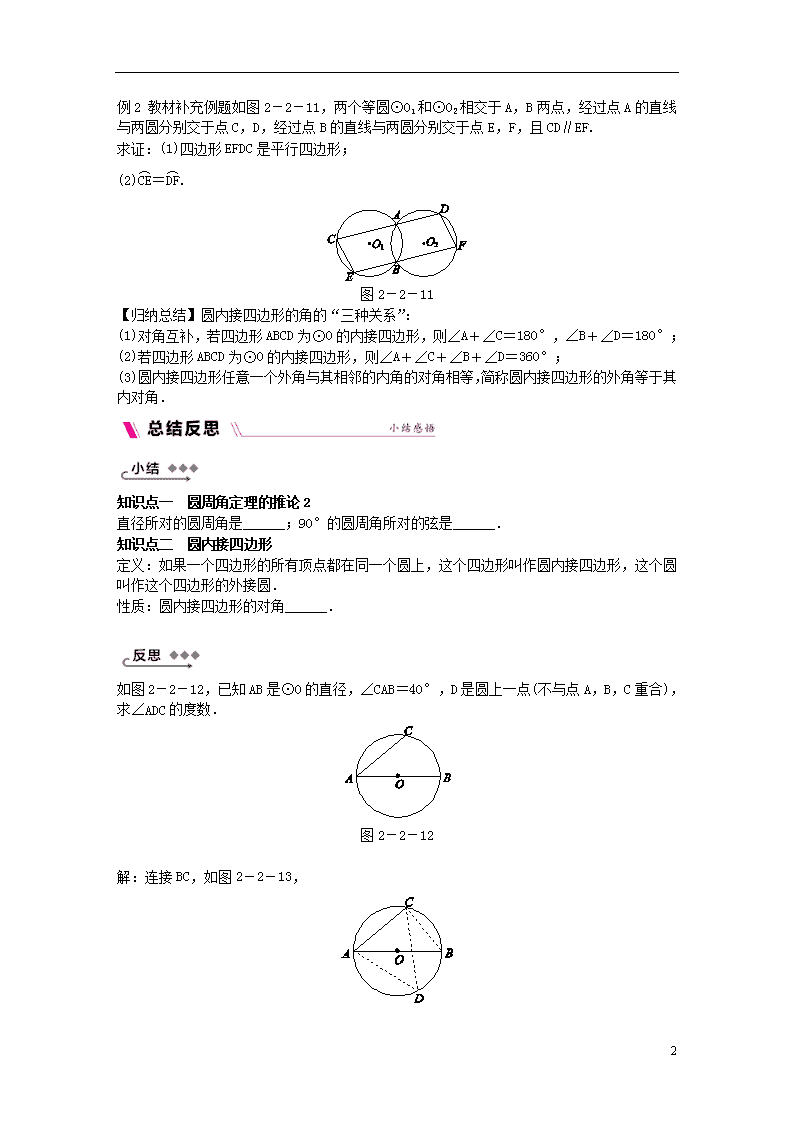
2.2.2 圆周角 第2课时 圆周角定理的推论2及圆内接四边形 知|识|目|标 1.通过特殊化思想探究直径所对的圆周角,理解圆周角定理的推论2. 2.在学习圆周角的基础上,结合图形理解圆内接四边形的概念,并探究圆内接四边形的性质. 目标一 理解圆周角定理的推论2并能计算或证明 例1 教材补充例题2017·宁波模拟如图2-2-10,AB是⊙O的直径,且AB=10,sin∠BAC=,D为优弧ABC上任意一点. 图2-2-10 (1)求AC的长; (2)求tan∠ADC的值. 【归纳总结】 1.圆周角定理及其推论中的转化思想: (1)弧是圆周角、圆心角的中介,通过弧可实现圆周角、圆心角之间的相互转化; (2)在同圆或等圆中,90°的圆周角和直径之间可以相互转化. 2.圆周角定理及其推论中常用的辅助线: 当题目中的条件出现直径时,通常作出直径所对的圆周角,得到直角,然后结合直角三角形的性质解决问题,即“见直径出直角”. 目标二 理解圆内接四边形及其性质 5 例2 教材补充例题如图2-2-11,两个等圆⊙O1和⊙O2相交于A,B两点,经过点A的直线与两圆分别交于点C,D,经过点B的直线与两圆分别交于点E,F,且CD∥EF. 求证:(1)四边形EFDC是平行四边形; (2)=. 图2-2-11 【归纳总结】圆内接四边形的角的“三种关系”: (1)对角互补,若四边形ABCD为⊙O的内接四边形,则∠A+∠C=180°,∠B+∠D=180°; (2)若四边形ABCD为⊙O的内接四边形,则∠A+∠C+∠B+∠D=360°; (3)圆内接四边形任意一个外角与其相邻的内角的对角相等,简称圆内接四边形的外角等于其内对角. 知识点一 圆周角定理的推论2 直径所对的圆周角是______;90°的圆周角所对的弦是______. 知识点二 圆内接四边形 定义:如果一个四边形的所有顶点都在同一个圆上,这个四边形叫作圆内接四边形,这个圆叫作这个四边形的外接圆. 性质:圆内接四边形的对角______. 如图2-2-12,已知AB是⊙O的直径,∠CAB=40°,D是圆上一点(不与点A,B,C重合),求∠ADC的度数. 图2-2-12 解:连接BC,如图2-2-13, 5 图2-2-13 ∵AB是⊙O的直径, ∴∠ACB=90°. ∵∠CAB=40°, ∴∠B=50°, ∴∠ADC=50°. 上述解答完整吗?若不完整,请补充完整. 5 教师详解详析 【目标突破】 例1 解:(1)连接BC.∵AB是⊙O的直径, ∴∠ACB=90°. ∵AB=10,sin∠BAC=, ∴BC=6,∴AC=8. (2)∵∠ADC=∠B, ∴tan∠ADC=tanB= = =. 例2 证明:(1)连接AB.∵四边形ABEC是⊙O1的内接四边形,∴∠BAC+∠E=180°. 又∵四边形ADFB是⊙O2的内接四边形, ∴∠BAD+∠F=180°. 又∵∠BAC+∠BAD=180°, ∴∠BAC=∠F, ∴∠E+∠F=180°,∴CE∥DF. 又∵CD∥EF, ∴四边形EFDC是平行四边形. (2)由(1)得四边形EFDC是平行四边形, ∴CE=DF. 又∵⊙O1与⊙O2等圆,∴=. 备选目标 圆心角、圆周角性质定理的综合运用 例 已知:如图所示,BC为半圆⊙O的直径,=,AC与BF相交于点M. (1)若∠FBC=α,求∠ACB的度数(用α表示); (2)过点A作AD⊥BC于点D,交BF于点E,求证:BE=EM. [解析] (1)利用=,探索∠ACB与∠FCB的关系;(2)欲证BE=EM,因为它们所在的三角形不全等,故找中间线段转换,注意到∠BAC=90°,因此选择AE为中间线段. 解:(1)如图,连接CF. ∵BC是⊙O的直径,∴∠F=90°. ∵∠FBC=α,∴∠FCB=90°-α. ∵=, 5 ∴∠5=∠ACF, ∴∠5=∠FCB=×(90°-α)=45°-α. 即∠ACB=45°-α. (2)证明:∵BC是⊙O的直径, ∴∠BAC=90°,即∠1+∠2=90°. ∵∠ADC=90°, ∴∠5+∠2=90°,∴∠1=∠5. ∵=, ∴∠5=∠4,∴∠1=∠4,∴BE=AE. 在Rt△ABM中, ∵∠1+∠2=90°,∠3+∠4=90°,∠1=∠4, ∴∠2=∠3,∴EM=AE,故BE=EM. [归纳总结] 在圆中求角的度数时,一般从与所求角相关的圆周角或圆心角入手,在进行角的转换时,还应特别注意“等弧”在角的转换中的重要过渡作用;在证明不是弦的两条线段相等时,一般考虑全等三角形或利用中间线段进行等量代换. 【总结反思】 [小结] 知识点一 直角 直径 知识点二 互补 [反思] 解答不完整.正确解法:连接BC,如图. ∵AB是⊙O的直径, ∴∠ACB=90°. ∵∠CAB=40°,∴∠B=50°. 当点D在优弧ABC上时,∠ADC=∠B=50°;当点D在劣弧AC上时,∠AD′C=180°-∠B=130°,∴∠ADC的度数为50°或130°. 5查看更多