数学理卷·2019届河北省衡水中学滁州分校高二下学期开学考试（2018-03）

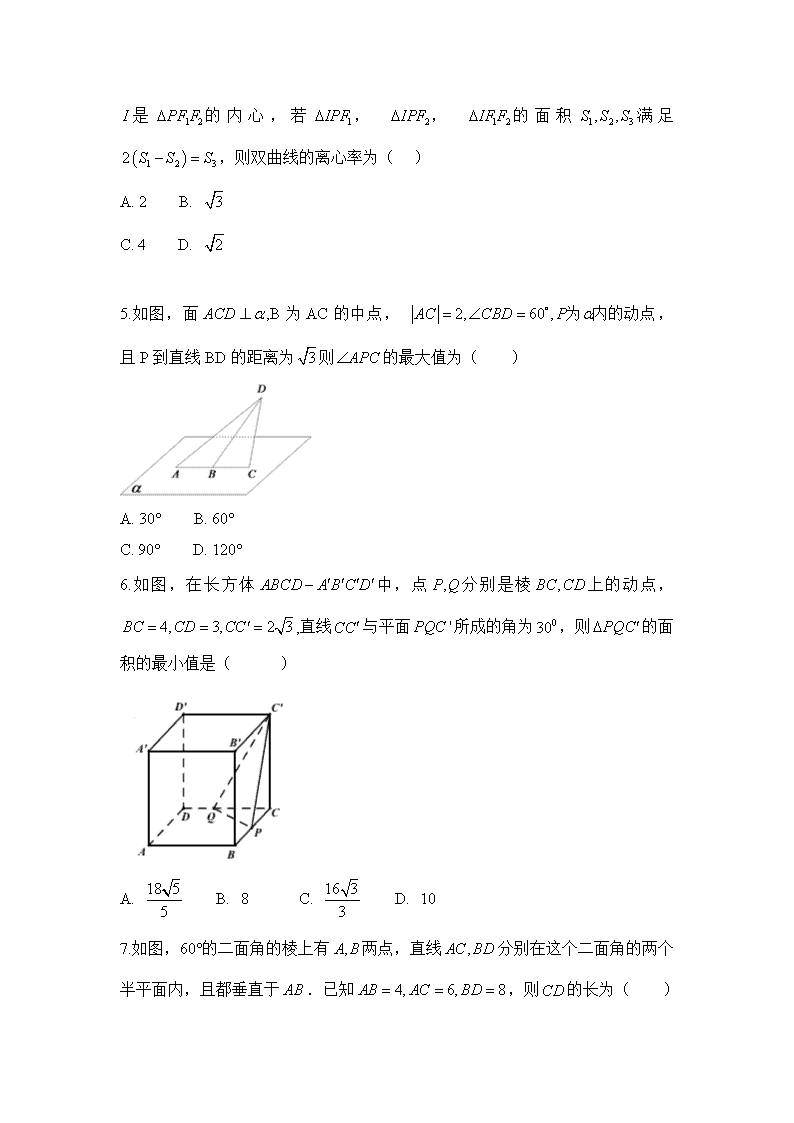
数学理卷·2019届河北省衡水中学滁州分校高二下学期开学考试（2018-03）

启用前绝密 河北省衡水中学滁州分校2017-2018学年下学期开学考试 高二（理科）数学 注意事项：‎ ‎1．你现在拿到的这份试卷是满分150分，作答时间为120分钟 ‎ ‎2．答题前请在答题卷上填写好自己的姓名、班级、考号等信息 ‎3．请将答案正确填写在答题卡上 第I卷（选择题60分）‎ 一、选择题(本大题共12个小题，每小题5分，共60分。) ‎ ‎1.已知为正数，则“”是“ ”的 （ ）‎ A. 充分不必要条件 B. 必要不充分条件 ‎ C. 充要条件 D. 既不充分也不必要条件 ‎2. 由命题“存在，使”是假命题，得的取值范围是，则实数的值是（ ）‎ A. 2 B. C. 1 D. ‎ ‎3. 如图，空间四边形中，点分别在上， ， ，则 ( )‎ A. B. ‎ C. D. ‎ ‎4. 设点为双曲线（， ）上一点， 分别是左右焦点， ‎ 是的内心，若， ， 的面积满足，则双曲线的离心率为（ ）‎ A. 2 B. ‎ C. 4 D. ‎ ‎5.如图，面,B为AC的中点， ，且P到直线BD的距离为则的最大值为（ ） ‎ A. 30° B. 60°‎ C. 90° D. 120°‎ ‎6.如图，在长方体中，点分别是棱上的动点， ,直线与平面所成的角为，则的面积的最小值是（ ）‎ A. B. C. D. ‎ ‎7.如图，60°的二面角的棱上有两点，直线分别在这个二面角的两个半平面内，且都垂直于．已知，则的长为（　　）‎ A. B. 7 ‎ C. D. 9‎ ‎8.已知是同一球面上的四个点，其中是正三角形， 平面， ，则该球的表面积为（ ）‎ A. B. C. D. ‎ ‎9.若直线与曲线有交点，则（ ）‎ A. 有最大值，最小值 B. 有最大值，最小值 C. 有最大值，最小值 D. 有最大值，最小值 ‎10.在四面体中， 分别是的中点，若，则（ ）‎ A. B. C. 1 D. 2‎ ‎11.若直线始终平分圆的周长，则 的最小值为 A. 1 B. 5 C. D. ‎ ‎12.如图，在长方体中， ， ，点在棱上，且，则当的面积最小时，棱的长为 A. B. C. D. ‎ 第II卷（非选择题 90分）‎ 二、填空题(本大题共4个小题，每小题5分，共20分。) ‎ ‎13. 已知是双曲线 的左焦点，若点，以线段的长为直径的圆与双曲线左，右两支在轴上方的交点分别为，则______.‎ ‎14. 如图所示，四棱锥的底面为矩形， ， ，且，记二面角的平面角为，若，则的取值范围是___________‎ ‎15.设抛物线的焦点为，过点的直线与抛物线相交于两点，与抛物线的准线相交于点， ，则与的面积之__________．‎ ‎16. 给出如下命題:‎ ‎①命题 “在中，若，则” 的逆命題为真命题;‎ ‎②若动点到两定点的距离之和为，则动点的轨迹为线段;‎ ‎③若为假命题，则都是假命題;‎ ‎④设，则“”是“”的必要不充分条件 ‎⑤若实数成等比数列，则圆锥曲线的离心率为; ‎ 其中所有正确命题的序号是_________.‎ 三、解答题(本大题共6个小题，70分。)‎ ‎17. (本题10分)如图，在四棱锥中， 平面, ,.‎ ‎(1)求证： ；‎ ‎(2)求多面体的体积.‎ ‎18. (本题12分)已知抛物线的焦点到准线的距离为，直线与抛物线交于两点，过这两点分别作抛物线 的切线，且这两条切线相交于点.‎ ‎（1）若的坐标为，求的值；‎ ‎（2）设线段的中点为，点的坐标为，过的直线与线段为直径的圆相切，切点为，且直线与抛物线交于两点，求的取值范围.‎ ‎19. (本题12分)在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点，‎ ‎（Ⅰ）求证：A1C1⊥BC1；‎ ‎（Ⅱ）求证：AC1∥平面CDB1．‎ ‎20. (本题12分)如图,直线与圆 且与椭圆相交于两点.‎ ‎(1)若直线恰好经过椭圆的左顶点,求弦长 ‎(2)设直线的斜率分别为,判断是否为定值,并说明理由 ‎(3)求，面积的最小值.‎ ‎21. (本题12分)如图,已知抛物线的焦点为，过的直线交抛物线于两点,过作准线的垂线,垂足为为原点.‎ ‎(1)求证: 三点共线；‎ ‎(2)求的大小.‎ ‎22. (本题12分)如图，在四棱锥中，，，，平面底面，.和分别是和的中点，求证：‎ ‎（Ⅰ）底面；‎ ‎（Ⅱ）平面；‎ ‎（Ⅲ）平面平面.‎ 河北省衡水中学滁州分校2017-2018学年下学期开学考试 高二（理科）数学 参考答案解析 一、选择题 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ C C ‎ B ‎ A B ‎ B C A C ‎ C ‎ A ‎ A ‎ ‎1.C ‎【解析】设，则在上单调递减。‎ 若，则，即；‎ 若，即，则有。‎ 综上可得“”是“ ”的充要条件。‎ 选C。‎ ‎2. C ‎【解析】命题“存在，使”是假命题，对任意的，有，为真命题，，又当时，取得最小值，的取值范围是，故选C.‎ ‎3. B ‎【解析】， ，故选B.‎ ‎4. A ‎【解析】‎ 如图,设圆I与的三边、、分别相切于点，连接，‎ 则，‎ 它们分别是, , 的高，‎ ‎∴，‎ ‎，‎ ‎，‎ 其中r是的内切圆的半径。‎ ‎∵，‎ ‎∴− = ，‎ 两边约去r得： ，‎ 根据双曲线定义,得，‎ ‎∴离心率为.‎ 故选：A.‎ ‎5.B ‎【解析】∵到直线的距离为 ‎∴空间中到直线的距离为的点构成一个圆柱面，它和面相交得一椭圆，即点在 内的轨迹为一个椭圆， 为椭圆中心， ， ，则 ‎∴为椭圆的焦点 ‎∵椭圆上的点关于两焦点的张角在短轴的端点取得最大值 ‎∴的最大值为 故选B ‎6.B ‎【解析】以C为原点，以CD，CB，CC′为坐标轴建立空间直角坐标系，如图所示： 则C（0，0，0）， 设P（0，a，0），Q（b，0，0），于是0＜a≤4，0＜b≤3． ‎ 设平面PQC′的一个法向量为 则 令z=1，得 ‎ a2b2≥2ab，解得ab≥8． ∴当ab=8时，S△PQC=4，棱锥C′-PQC的体积最小， ∵直线CC′与平面PQC′所成的角为30°，∴C到平面PQC′的距离d=2 ‎ ‎∵VC′-PQC=VC-PQC′， ‎ 故选B ‎7.C ‎【解析】7.∵， ，∴，∵，∴ ，∴，故选C.‎ ‎8.A ‎【解析】‎ 由题意画出几何体的图形如图，把扩展为三棱柱，上下底面中心连线的中点与A的距离为球的半径，‎ ‎∵， 是正三角形，‎ 所以 ‎，‎ 所求球的表面积为： 。‎ 故选A。‎ ‎9.C ‎【解析】如图所示，曲线表示以为圆心， 为半径的圆（轴上方部分），‎ 当直线与曲线相切时， ‎ 有最大值，最小值 故答案选 ‎10.C ‎【解析】如图所示， 连接，∵、分别是、的中点，∴， ∴， 又，∴，故选C.‎ ‎11.A ‎【解析】由题意可得：直线经过圆心，所以；‎ 则，所以应选D．‎ ‎12.A ‎【解析】建立如图所示的空间直角坐标系，则，所以，由题设，即，也即；又，故（当且仅当 取等号），此时即，应选答案A。‎ 二、填空题 ‎13 .‎ ‎【解析】.由于F为双曲线的左焦点，在x轴上F点的右侧有一点A，‎ 以FA为直径的圆与双曲线左、右两支在x轴上方的交点分别为M，N，‎ 不妨设A为椭圆的右焦点，则F（﹣5，0），A（5，0），|FN|﹣|NA|=8，‎ 由双曲线的对称性得到|FM|=|NA|，‎ ‎∴|FN|﹣|FM|=8‎ 则=‎ ‎14． ‎ ‎【解析】由题意易得： ，∴△CPA≌△CBA，‎ 过P作PO⊥AC于O点，连OB，则OB⊥AC，‎ ‎∴∠POB为二面角的平面角 ‎，‎ 即，又 ‎∴的取值范围是 ‎15.‎ ‎【解析】‎ 由题意可得抛物线的焦点的坐标为，准线方程为。‎ 如图，设，过A,B分别向抛物线的准线作垂线，垂足分别为E,N，则 ‎，解得。‎ 把代入抛物线，解得。‎ ‎∴直线AB经过点与点，‎ 故直线AB的方程为，代入抛物线方程解得。‎ ‎∴。‎ 在中， ，‎ ‎∴‎ ‎∴。答案： ‎ ‎16. .①②④‎ ‎【解析】①命题“在中,若,则”的逆命题为“在中,若,则”,是真命题；②若动点到两定点 的距离之和为,则动点的轨迹为线段,正确,原因是只有线段上的点到定点的距离之和为；③若为假命题,则都是假命题,错误,原因是只要中有一个是假命题,就有为假命题；④设,由能得到,反之由不一定有.则“”是“”的必要不充分条件；⑤若实数成等比数列,则,.若,圆锥曲线表示焦点在轴上的双曲线,此时,,,圆锥曲线的离心率为,命题⑤错误.因此，本题正确答案是①②④.‎ 三、简答题 ‎17.‎ ‎(I) 面面 面 又面 ‎(II)解：连接 平面 为直角三角形且为直角.‎ ‎18. （1）由抛物线的焦点到准线的距离为，得，‎ 则抛物线的方程为.‎ 设切线的方程为，代入得，‎ 由得，‎ 当时，点的横坐标为，‎ 则，‎ 当时，同理可得.‎ 综上得。‎ ‎（2）由（1）知， ，‎ 所以以线段为直径的圆为圆，‎ 根据对称性，只要探讨斜率为正数的直线即可，‎ 因为为直线与圆的切点，‎ 所以， ，‎ 所以，‎ 所以，‎ 所以直线的方程为，‎ 由消去整理得，‎ 因为直线与圆相交，所以。‎ 设，则，‎ 所以，‎ 所以，‎ 设，因为，所以，‎ 所以，‎ 所以.‎ ‎19. ‎ 证明(法一: 故有,A. 法二: ;由直三棱柱;;平面; 平面,平面, 平面,‎ ‎(连接相交于点O,连OD,易知// , 平面 , 平面,故//平面.‎ ‎20.‎ ‎（1）由题意直线斜率存在，设直线 因为直线与圆相切，‎ 所以 解得 当时，由解得，所以 当时，同理 所以。‎ ‎（2）（ⅰ）当直线的斜率不存在时，得；‎ ‎（ⅱ）当的斜率存在时，设直线 ‎ 因为直线与圆相切，‎ 所以 整理得所以①，‎ 由消去y整理得，‎ 由直线与圆相交得 设 则 ，②‎ 所以③，‎ 将①②代入③式得 综上可得 ‎ ‎（3）由（2）知 记直线与圆的切点为 设 所以，‎ 则 所以当时， .‎ ‎21.‎ ‎（1）设直线 ‎ 由消去y整理得 ‎ 设 则 因为 ‎ 所以，‎ 所以，‎ 又线段有公共点， ‎ 所以三点共线. ‎ ‎（2）因为 所以，‎ 所以，‎ 所以 ‎22.‎ ‎（Ⅰ）因为平面底面，且垂直于这两个平面的交线， ‎ 所以底面.‎ ‎（Ⅱ）因为，，是的中点，‎ 所以，且.‎ 所以为平行四边形.‎ 所以，.‎ 又因为平面，平面，‎ 所以平面.‎ ‎（Ⅲ）因为，并且为平行四边形，‎ 所以,.‎ 由（Ⅰ）知底面，‎ 所以，‎ 所以平面.‎ 所以.‎ 因为和分别是和的中点，‎ 所以.‎ 所以.‎ 所以平面.‎ 所以平面平面.‎