- 2021-06-19 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020版高考数学二轮复习 专题六 统计与概率 专题对点练20 统计与概率 文
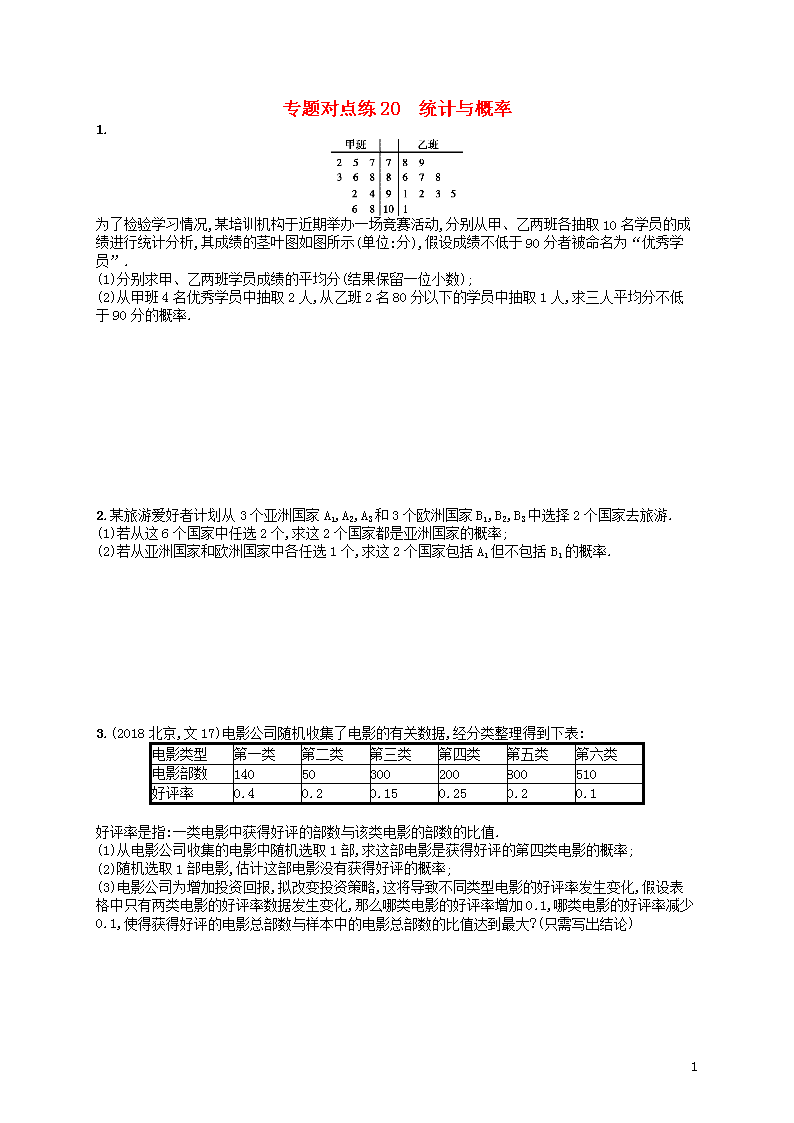
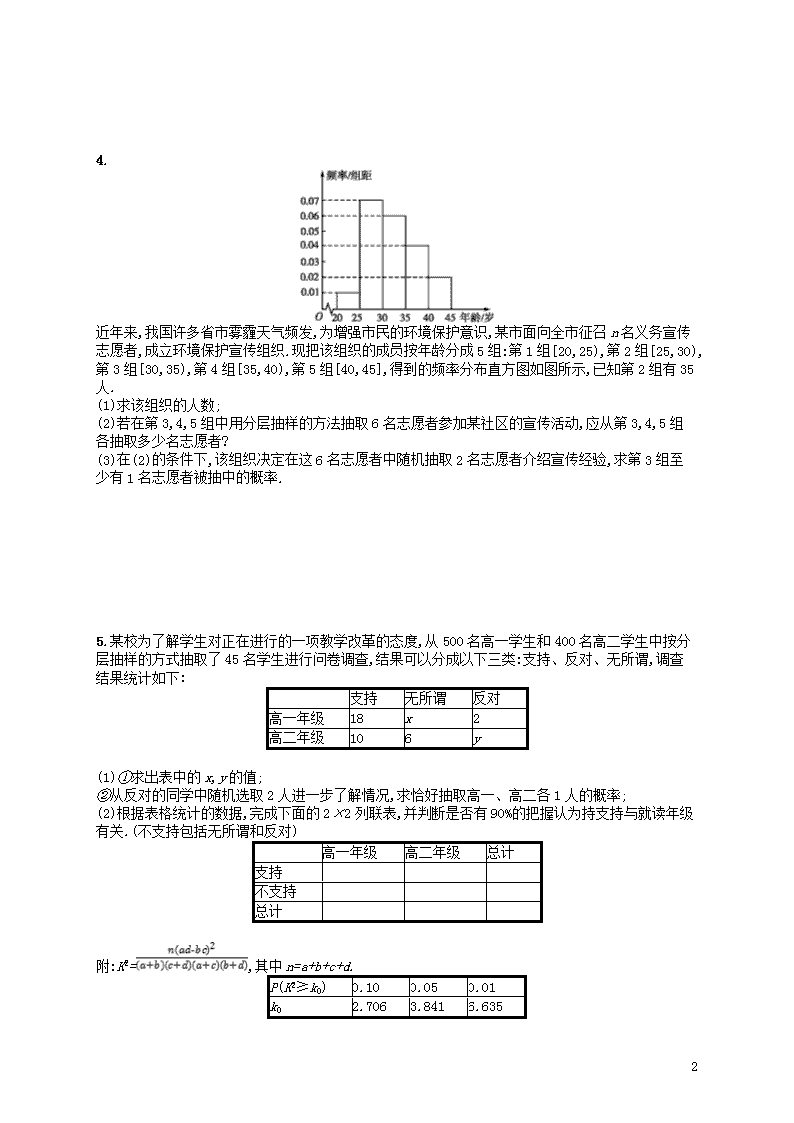
专题对点练20 统计与概率 1. 为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者被命名为“优秀学员”. (1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数); (2)从甲班4名优秀学员中抽取2人,从乙班2名80分以下的学员中抽取1人,求三人平均分不低于90分的概率. 2.某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游. (1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率; (2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率. 3.(2018北京,文17)电影公司随机收集了电影的有关数据,经分类整理得到下表: 电影类型 第一类 第二类 第三类 第四类 第五类 第六类 电影部数 140 50 300 200 800 510 好评率 0.4 0.2 0.15 0.25 0.2 0.1 好评率是指:一类电影中获得好评的部数与该类电影的部数的比值. (1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率; (2)随机选取1部电影,估计这部电影没有获得好评的概率; (3)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化,假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论) 5 4. 近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人. (1)求该组织的人数; (2)若在第3,4,5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动,应从第3,4,5组各抽取多少名志愿者? (3)在(2)的条件下,该组织决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第3组至少有1名志愿者被抽中的概率. 5.某校为了解学生对正在进行的一项教学改革的态度,从500名高一学生和400名高二学生中按分层抽样的方式抽取了45名学生进行问卷调查,结果可以分成以下三类:支持、反对、无所谓,调查结果统计如下: 支持 无所谓 反对 高一年级 18 x 2 高二年级 10 6 y (1)①求出表中的x,y的值; ②从反对的同学中随机选取2人进一步了解情况,求恰好抽取高一、高二各1人的概率; (2)根据表格统计的数据,完成下面的2×2列联表,并判断是否有90%的把握认为持支持与就读年级有关.(不支持包括无所谓和反对) 高一年级 高二年级 总计 支持 不支持 总计 附:K2=,其中n=a+b+c+d. P(K2≥k0) 0.10 0.05 0.01 k0 2.706 3.841 6.635 5 5 专题对点练20答案 1.解 (1)甲班学员的平均分为88.1;乙班学员的平均分为89.0. (2)所有抽取情况为:92,94,78;92,94,79;92,106, 78;92,106,79;92,108,78;92,108,79;94,106,78;94,106,79;94,108,78;94,108,79;106,108,78;106,108,79.总共有12种. 这12种情况中,平均分不低于90分的情况有10种.所以三人平均分不低于90分的概率为. 2.解 (1)由题意知,从6个国家中任选两个国家,其一切可能的结果组成的基本事件有: {A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A1,B3},{A2,B1},{A2,B2},{A2,B3},{A3,B1},{A3,B2},{A3,B3},{B1,B2},{B1,B3},{B2,B3},共15个. 所选两个国家都是亚洲国家的事件所包含的基本事件有: {A1,A2},{A1,A3},{A2,A3},共3个,则所求事件的概率为P=. (2)从亚洲国家和欧洲国家中各任选一个,其一切可能的结果组成的基本事件有: {A1,B1},{A1,B2},{A1,B3},{A2,B1},{A2,B2},{A2,B3},{A3,B1},{A3,B2},{A3,B3},共9个. 包括A1但不包括B1的事件所包含的基本事件有: {A1,B2},{A1,B3},共2个, 则所求事件的概率为P=. 3.解 (1)由题意知,样本中电影的总部数是140+50+300+200+800+510=2 000. 第四类电影中获得好评的电影部数是200×0.25=50,故所求概率为=0.025. (2)(方法一)由题意知,样本中获得好评的电影部数是140×0.4+50×0.2+300×0.15+200×0.25+800×0.2+510×0.1=56+10+45+50+160+51=372. 故估计所求概率为1-=0.814. (方法二)设“随机选取1部电影,这部电影没有获得好评”为事件B. 没有获得好评的电影共有140×0.6+50×0.8+300×0.85+200×0.75+800×0.8+510×0.9=1 628(部). 由古典概型概率公式,得P(B)==0.814. (3)第五类电影的好评率增加0.1,第二类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大. 4.解 (1)由题意,得第2组的人数为35=5×0.07×n,得到n=100,故该组织有100人. (2)第3组的人数为0.06×5×100=30,第4组的人数为0.04×5×100=20,第5组的人数为0.02×5×100=10, 所以第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:第3组×6=3;第4组×6=2;第5组×6=1. 所以应从第3,4,5组中分别抽取3人,2人,1人. (3)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的1名志愿者为C1, 则从6名志愿者中抽取2名志愿者有(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种. 其中第3组的3名志愿者A1,A2,A3至少有一名志愿者被抽中的有(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2, B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),共有12种. 则第3组至少有1名志愿者被抽中的概率为. 5.解 (1)①由题可得x=5,y=4. ②假设高一持反对的编号为A1,A2,高二持反对的编号为B1,B2,B3,B4, 则选取两人的所有结果为(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A2, B1),(A2,B2),(A2,B3),(A2,B4),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4). 5 ∴恰好抽取高一、高二各1人包含8个事件,∴所求概率P=. (2)列联表如图: 高一年级 高二年级 总计 支 持 18 10 28 不支持 7 10 17 总 计 25 20 45 K2==2.288<2.706. 故没有90%的把握认为持支持与就读年级有关. 5查看更多