- 2021-06-18 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年高考天津卷数学真题试卷(含答案)
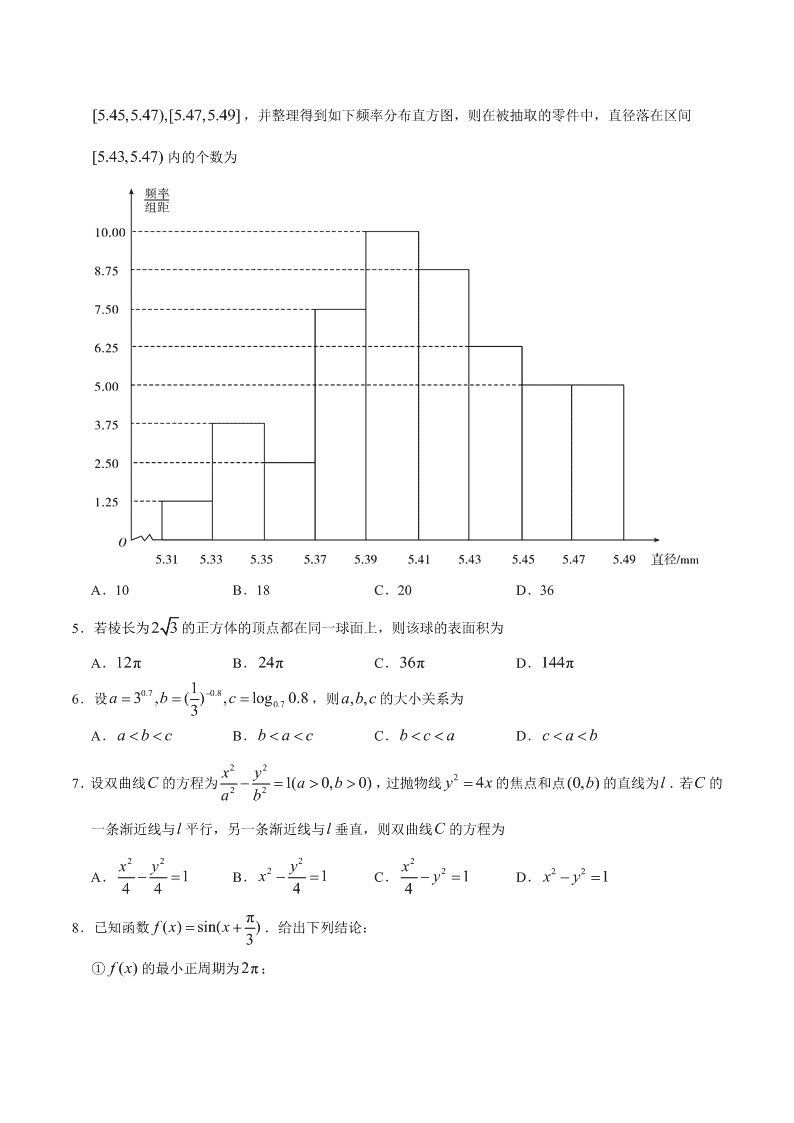
2020 年高考天津卷数学真题试卷(含答案) 第Ⅰ卷 注意事项: 1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂 其他答案标号。 2.本卷共 9 小题,每小题 5 分,共 45 分. 参考公式: ·如果事件 A 与事件 B 互斥,那么 ()()()PABPAPB. ·如果事件 A 与事件 B 相互独立,那么 ()()()PABPAPB . ·球的表面积公式 24πSR ,其中 R 表示球的半径. 一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设全集 {3,2,1,0,1,2,3}U ,集合 {1,0,1,2},{3,0,2,3}AB ,则 UAB∩ ð A. { 3 ,3} B. { 0 ,2 } C. { 1,1} D.{3,2,1,1,3} 2.设 a R ,则“ 1a ”是“ 2aa ”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 3.函数 2 4 1 xy x 的图象大致为 A B C D 4.从一批零件中抽取 80 个,测量其直径(单位:mm ), 将所得数据分为 9 组:[5.31,5.33),[5.33,5.35), , [5.45,5.47),[5.47,5.49],并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间 [ 5 . 4 3 ,5 . 4 7 ) 内的个数为 A.10 B.18 C.20 D.36 5.若棱长为 23的正方体的顶点都在同一球面上,则该球的表面积为 A. 12 π B. 24 π C. 36 π D. 144 π 6.设 0.70.8 0.7 13,(),log0.83abc ,则 ,,abc的大小关系为 A. abc B. bac C. bca D. cab 7.设双曲线 C 的方程为 22 221(0,0)xy abab ,过抛物线 2 4yx 的焦点和点(0, )b 的直线为 l .若 C 的 一条渐近线与l 平行,另一条渐近线与l 垂直,则双曲线C 的方程为 A. 22 144 xy B. 2 2 14 yx C. 2 2 14 x y D. 221xy 8.已知函数 π( ) sin( )3f x x.给出下列结论: ① ()fx的最小正周期为 2π; ② π()2f 是 ()fx的最大值; ③把函数 s i nyx 的图象上所有点向左平移 π 3 个单位长度,可得到函数 ()y f x 的图象. 其中所有正确结论的序号是 A.① B.①③ C.②③ D.①②③ 9.已知函数 3 ,0,() ,0. xxfx xx 若函数 2( ) ( ) 2 ( )g x f x kx x k R 恰有 4 个零点,则 k 的取值范围是 A. 1(,)(22,)2 B. 1(,)(0,22)2 C.( ,0) (0,2 2) D.( ,0) (2 2, ) 第Ⅱ卷 注意事项: 1.用黑色墨水的钢笔或签字笔将答案写在答题卡上. 2.本卷共 11 小题,共 105 分. 二.填空题:本大题共 6 小题,每小题 5 分,共 30 分.试题中包含两个空的,答对 1 个的给 3 分,全部答 对的给 5 分. 10. i 是虚数单位,复数 8i 2i _________. 11.在 5 2 2()x x 的展开式中, 2x 的系数是_________. 12.已知直线 380xy 和圆 222 (0)xyrr 相交于 ,AB两点.若 | | 6AB ,则 r 的值为 _________. 13.已知甲、乙两球落入盒子的概率分别为 1 2 和 1 3 .假定两球是否落入盒子互不影响,则甲、乙两球都落 入盒子的概率为_________;甲、乙两球至少有一个落入盒子的概率为_________. 14.已知 0,0a b,且 1ab ,则 1 1 8 22a b a b 的最小值为_________. 15.如图,在四边形 ABCD中, 60 , 3B AB , 6BC ,且 3, 2AD BC AD AB ,则实数 的值为_________,若 ,MN是线段 BC 上的动点,且||1MN ,则 DM DN 的最小值为_________. 三.解答题:本大题共 5 小题,共 75 分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分 14 分) 在 ABC△ 中,角 ,,A B C 所对的边分别为 ,,abc.已知 22,5,13abc . (Ⅰ)求角 C 的大小; (Ⅱ)求 s i n A 的值; (Ⅲ)求 πsin(2 )4A 的值. 17.(本小题满分 15 分) 如图,在三棱柱 111A B C A BC 中, 1CC 平面 ,,2ABCACBCACBC , 1 3CC ,点 ,DE 分别在棱 1AA 和棱 1CC 上,且 2,1,ADCEM为棱 11AB 的中点. (Ⅰ)求证: 11C M B D ; (Ⅱ)求二面角 1BB ED的正弦值; (Ⅲ)求直线 AB 与平面 1DB E 所成角的正弦值. 18.(本小题满分 15 分) 已知椭圆 22 221( 0)xy abab 的一个顶点为 (0, 3)A ,右焦点为 F ,且| | | |OA OF ,其中O 为原 点. (Ⅰ)求椭圆的方程; (Ⅱ)已知点 C 满足 3O C O F ,点 B 在椭圆上( B 异于椭圆的顶点),直线 AB 与以 C 为圆心的圆 相切于点 P ,且 P 为线段 AB 的中点.求直线 AB 的方程. 19.(本小题满分 15 分) 已知 na 为等差数列, nb 为等比数列, 1 1 5 4 3 5 4 31, 5 , 4a b a a a b b b . (Ⅰ)求 na 和 nb 的通项公式; (Ⅱ)记 的前 n 项和为 nS ,求证: 2* 21nnnSSSnN ; (Ⅲ)对任意的正整数 n ,设 2 1 1 32,, ,. nn nn n n n abnaac a nb 为奇数 为偶数 求数列 nc 的前 2 n 项和. 20.(本小题满分 16 分) 已知函数 3()ln()fxxkx k R , ()fx 为 ()fx的导函数. (Ⅰ)当 6k 时, (i)求曲线 ()y f x 在点(1, (1))f 处的切线方程; (ii)求函数 9()()()gxfxfx x 的单调区间和极值; (Ⅱ)当 3k 时,求证:对任意的 12,[1,)xx ,且 12xx ,有 1212 122 fxfxfxfx xx . 2020 年普通高等学校招生全国统一考试(天津卷) 数学参考解答 一.选择题:每小题 5 分,满分 45 分. 1.C 2.A 3.A 4.B 5.C 6.D 7.D 8.B 9.D 二.填空题:每小题 5 分,满分 30 分.试题中包含两个空的,答对 1 个的给 3 分,全部答对的给 5 分. 10. 3 2 i 11.10 12.5 13. 1 6 ; 2 3 14.4 15. 1 6 ; 13 2 三.解答题 16.满分 14 分. (Ⅰ)解:在 ABC△ 中,由余弦定理及 22,5,13abc ,有 2 2 2 2cos 22 a b cC ab .又 因为 ( 0 , π )C ,所以 π 4C . (Ⅱ)解:在 ABC△ 中,由正弦定理及 π ,22,134Cac ,可得 sin 2 13sin 13 aCA c. (Ⅲ)解:由 ac 及 213sin 13A ,可得 2 313cos1sin 13AA , 进而 2125sin 22sincos,cos 22cos11313AAAAA . 所以, π π π 1225217 2sin(2) sin 2 coscos 2 sin44413213226AAA . 17.满分 15 分. 依题意,以 C 为原点,分别以 1,,CACBCC 的方向为 x 轴, y 轴, z 轴的正方向建立空间直角坐标系 (如图),可得 1(0,0,0),(2,0,0),(0,2,0),(0,0,3)CABC , 11(2,0,3),(0,2,3),(2,0,1),(0,0,2)ABDE , (1,1,3)M . (Ⅰ)证明:依题意, 1 ( 1 ,1 ,0)CM , 1 (2 , 2 , 2)BD ,从而 112200CMBD ,所以 11C M B D . (Ⅱ)解:依题意, (2,0,0)CA 是平面 1B B E 的一个法向量, 1 (0 ,2 ,1 )EB , (2,0, 1)ED .设 ( , , )x y zn 为平面 1D B E 的法向量,则 1 0, 0, EB ED n n 即 2 0 , 2 0 . yz xz 不妨设 1x ,可得 (1, 1,2 )n . 因此有 | || 6cos , 6|A CA C CA nn n ,于是 30sin , 6CA n . 所以,二面角 1B B E D的正弦值为 30 6 . (Ⅲ)解:依题意, ( 2 ,2 ,0 )AB .由(Ⅱ)知 (1, 1,2 )n 为平面 1D B E 的一个法向量,于是 3cos, 3|||| ABAB AB nn n . 所以,直线 AB 与平面 1D B E 所成角的正弦值为 3 3 . 18.满分 15 分. (Ⅰ)解:由已知可得 3b .记半焦距为c ,由||||OFOA 可得 3cb.又由 2 2 2a b c,可得 2 18a .所以,椭圆的方程为 22 1189 xy. (Ⅱ)解:因为直线 AB 与以 C 为圆心的圆相切于点 P ,所以 ABCP .依题意,直线 AB 和直线 CP 的斜率均存在.设直线 AB 的方程为 3ykx.由方程组 22 3, 1,189 ykx xy 消去 y ,可得 2221120kxkx ,解得 0x ,或 2 12 21 kx k .依题意,可得点 B 的坐标为 2 22 12 6 3,2 1 2 1 kk kk .因 为 P 为线段 AB 的中点,点 A 的坐标为 (0,3) ,所 以点 P 的坐标为 22 63,2121 k kk .由3OC OF , 得点 C 的坐标为 (1,0 ) ,故直线 CP 的斜率为 2 2 3 021 6 121 k k k ,即 2 3 2 6 1kk .又因为 A B C P ,所以 2 3 1261k kk ,整理得 22 3 1 0kk ,解得 1 2k ,或 1k . 所以,直线 AB 的方程为 1 32yx,或 3yx. 19.满分 15 分. (Ⅰ)解:设等差数列 na 的公差为 d ,等比数列 nb 的公比为 q .由 1 1a , 543 5a a a,可 得 1d ,从而 na 的通项公式为 nan .由 1543 1,4bbbb ,又 0q ,可得 2 4 4 0qq , 解得 2q ,从而 nb 的通项公式为 12 n nb . (Ⅱ)证明:由( Ⅰ)可得 ( 1) 2n nnS ,故 2 1 ( 1)( 2)( 3)4nnS S n n n n , 222 1 1 ( 1) 24nS n n , 从而 2 21 1 (1)(2)02nnnSSSnn ,所以 2 21nnnS S S . (Ⅲ)解:当 n 为奇数时, 1 1 1 2 32 (3 2)2 2 2 ( 2) 2 n n n nn n nn abnc a a n n n n ;当 n 为偶数时, 1 1 1 2 n n n n a nc b . 对任意的正整数 n ,有 2222 21 11 222 1212121 kknnn k kk c kkn , 和 2 23 11 2113521 44444 nn k kn kk knc . ① 由①得 2 231 1 1132321 44444 n k nn k nnc . ② 由①②得 2 211 1 21131 22 2 11 2 1 44 144 4444 4 1 4 nn k nnn k nnc ,从而得 2 1 5 6 5 9 9 4 n k n k nc . 因此, 2 2 1 2 1 1 1 4 6 5 4 2 1 9 4 9 nn n n k k k n k k k nc c c n . 所以,数列 nc 的前 2 n 项和为 4654 21949 n n n n . 20.满分 16 分. (Ⅰ)( i)解:当 6k 时, 3( ) 6l nf x x x ,故 2 6( ) 3f x x x .可得 (1) 1f , (1) 9f ,所 以曲线 ()y f x 在点 (1, (1) )f 处的切线方程为 1 9 ( 1 )yx ,即 98yx. (ii)解:依题意, 32 3()36ln,(0,)gxxxxx x .从而可得 2 2 63()36gxxx xx , 整理可得 3 2 3(1)(1)() xxgx x .令 ( ) 0gx ,解得 1x . 当 x 变化时, ( ), ( )g x g x 的变化情况如下表: x (0 ,1) 1 (1, ) ()gx - 0 + ()gx ↘ 极小值 ↗ 所以,函数 ()gx 的单调递减区间为 (0 ,1) ,单调递增区间为 ( 1, ) ; ()gx 的极小值为 ( 1 ) 1g ,无极 大值. (Ⅱ)证明:由 3( ) lnf x x k x ,得 2()3 kfxx x . 对任意的 12,[1,)xx ,且 12xx ,令 1 2 (1)x ttx ,则 121212 2xxfxfxfxfx 2 2 3 3 1 1 2 1 2 1 2 1 2 2 3 3 2 ln xkkx x x x x x kx x x 3322 121 121 21 2 212 332 ln x xxx xx xx x kk xxx 3 32 2 133 12lnx tttk tt t . ① 令 1( ) 2ln , [1, )h x x x xx .当 1x 时, 2 2 1 2 1( ) 1 1 0hx x x x ,由此可得 ()hx在 [1, ) 单调递增,所以当 1t 时, ( ) (1)h t h ,即 1 2l n 0ttt . 因为 2 1x , 323 331(1)0,3ttttk , 所以, 33232 2 113312ln(331)32lnxtttkttttttt tt 23 36ln3 1ttt t . ② 由(Ⅰ)( ii)可知,当 1t 时, ( ) (1)g t g ,即 32 336ln1ttt t , 故 23 336ln10ttt t . ③ 由①②③可得 121212 20xxfxfxfxfx .所以,当 3k 时,对任意的 12, [ 1, )xx ,且 12xx ,有 1212 122 fxfxfxfx xx .查看更多