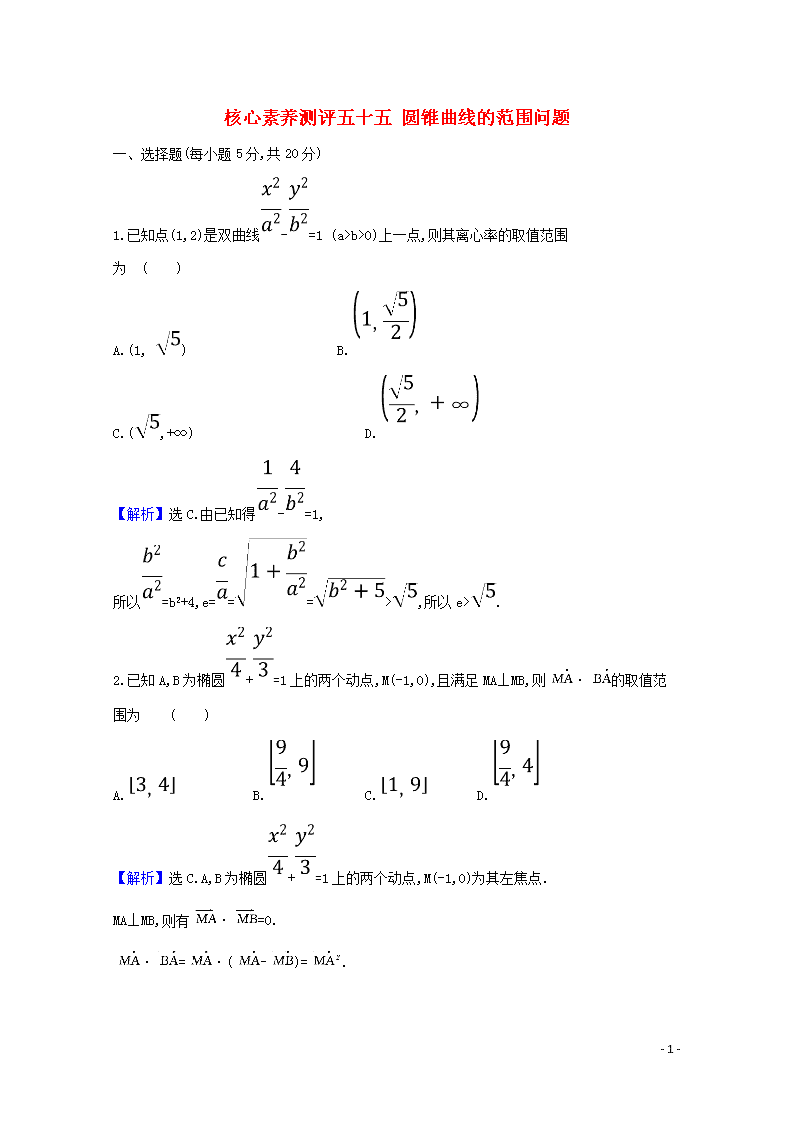2021版高考数学一轮复习核心素养测评五十五圆锥曲线的范围问题苏教版

2021版高考数学一轮复习核心素养测评五十五圆锥曲线的范围问题苏教版

核心素养测评五十五 圆锥曲线的范围问题 一、选择题(每小题5分,共20分)‎ ‎1.已知点(1,2)是双曲线-=1 (a>b>0)上一点,则其离心率的取值范围 为 (　　)‎ A.(1, ) B.‎ C.(,+∞) D.‎ ‎【解析】选C.由已知得-=1,‎ 所以=b2+4,e===>,所以e>.‎ ‎2.已知A,B为椭圆+=1上的两个动点,M(-1,0),且满足MA⊥MB,则·的取值范围为 (　　)‎ A. B.　 C.　 D.‎ ‎【解析】选C.A,B为椭圆+=1上的两个动点,M(-1,0)为其左焦点.‎ MA⊥MB,则有·=0.‎ ‎·=·(-)=.‎ - 7 -‎ 设A(x,y),则y2=3(1-).‎ ‎=(x+1)2+y2=(x+1)2+3(1-)=x2+2x+4=(x+4)2.‎ 由x∈[-2,2],得=(x+4)2∈[1,9].‎ ‎3.已知椭圆C1:+=1(a>b>0)与圆C2:x2+y2=b2,若在椭圆C1上存在点P,使得由点P所作的圆C2的两条切线互相垂直,则椭圆C1的离心率的取值范围为(　　)‎ A. B. ‎ C.　 D.‎ ‎【解析】选C.由椭圆上长轴端点向圆作两条切线PA、PB,则两切线形成的角为∠APB,若椭圆C1上存在点P令切线互相垂直,则只需∠APB≤90°,即α=∠APO≤45°,所以sin α=≤sin 45°=,解得a2≤‎2c2,所以e2≥,即e≥.而04),点A(-2,2)是椭圆内一点,B(0,-2),若椭圆上存在一点P,使得|PA|+|PB|=8,则m的范围是________;当m取得最大值时,椭圆的离心率为________. ‎ ‎【解析】显然椭圆的焦点在y轴上,设椭圆的半焦距为c,则c==2,‎ 故B为椭圆的下焦点,设椭圆的上焦点为F(0,2),‎ 则由椭圆定义可知|PF|+|PB|=‎2a,‎ 因为|PA|+|PB|=8,所以|PA|=8-|PB|,‎ 于是||PA|-|PF||=|8-|PB|-|PF||=|8‎-2a|,‎ 又||PA|-|PF||≤|AF|=2,‎ 所以|8‎-2a|≤2,解得:3≤a≤5,即3≤≤5,‎ 所以9≤m≤25.‎ 又A(-2,2)在椭圆内部,所以+<1,‎ 又m>4,‎ 解得m>6+2.‎ 综上可得:6+20)上一点M(m,9)到其焦点F的距离为10. ‎ ‎(1)求抛物线C的方程.‎ ‎(2)设过焦点F的直线l与抛物线C交于A,B两点,且抛物线在A,B两点处的切线分别交x轴于P,Q两点,求|AP|·|BQ|的取值范围.‎ ‎【解析】(1)已知M(m,9)到焦点F的距离为10,则点M到准线的距离为10.‎ 因为抛物线的准线为y=-,所以9+=10,‎ 解得p=2,所以抛物线的方程为x2=4y.‎ ‎(2)由已知可判断直线l的斜率存在,设斜率为k,‎ 因为F(0,1),则l:y=kx+1.‎ 设A,B,‎ 由消去y得,x2-4kx-4=0,所以x1+x2=4k,x1x2=-4.‎ 由于抛物线C也是函数y=x2的图象,且y′=x,则PA:y-=x1(x-x1).‎ 令y=0,解得x=x1,所以P,‎ 从而|AP|=.‎ 同理可得|BQ|=,‎ 所以|AP|·|BQ|=‎ ‎=‎ - 7 -‎ ‎=2.因为k2≥0,所以|AP|·|BQ|的取值范围为[2,+∞).‎ ‎8.已知椭圆C1,抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上各取两个点,其坐标分别是(3,-2),(-2,0),(4,-4),. ‎ ‎(1)求C1,C2的标准方程.‎ ‎(2)过点M(0,2)的直线l与椭圆C1交于不同的两点A,B,且∠AOB为钝角(其中O为坐标原点),求直线l的斜率k的取值范围.‎ ‎【解析】(1)由题意,抛物线的顶点为原点,设椭圆方程为+=1(a>b>0),‎ 所以点(-2,0)一定在椭圆上,且a=2,则椭圆上任何点的横坐标的绝对值都小于等于2,‎ 所以也在椭圆上,+=1,b2=1,故椭圆标准方程为+y2=1,‎ 所以点(3,-2)、(4,-4)在抛物线上,且抛物线开口向右,设其方程为y2=2px(p>0),12=6p,p=2,‎ 所以方程为y2=4x.‎ ‎(2)①当直线l斜率不存在时,易知A,O,B三点共线,不符合题意.‎ ‎②当l斜率存在时,设l:y=kx+2,A(x1,x2),‎ B(x2,y2),x2+4(kx+2)2-4=0,(4k2+1)x2+16kx+12=0,‎ 令Δ=(16k)2-48(4k2+1)>0,‎ ‎256k2-192k2-48>0,64k2>48,k<-或k>,‎ ‎=(x1,y1),=(x2,y2),x1+x2=,x1x2=,‎ y1y2=(kx1+2)(kx2+2)‎ - 7 -‎ ‎=k2x1x2+2k(x1+x2)+4‎ ‎=-+=,‎ 令·=x1x2+y1y2=<0,‎ 即4k2>16,k<-2或k>2.‎ 综上:k<-2或k>2.‎ - 7 -‎