九年级数学上册第三章概率的进一步认识1用树状图或表格求概率第1课时用树状图或表格求概率教学课件新版北师大版

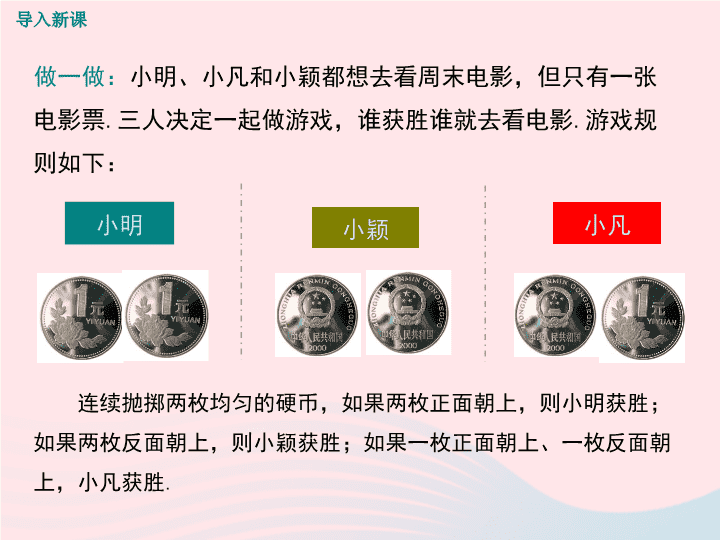
九年级数学上册第三章概率的进一步认识1用树状图或表格求概率第1课时用树状图或表格求概率教学课件新版北师大版

3.1 用树状图或表格求概率 第三章 概率的进一步认识 第 1 课时 用树状图和表格求概率 导入新课 讲授新课 当堂练习 课堂小结 1. 会用画树状图或列表的方法计算简单随机事件发生的概率 ; （重点） 2. 能用画树状图或列表的方法不重不漏地列举事件发生的所有可 能情况 . （难点） 3. 会用概率的相关知识解决实际问题 . 学习目标 做一做： 小明、小凡和小颖都想去看周末电影，但只有一张电影票 . 三人决定一起做游戏，谁获胜谁就去看电影 . 游戏规则如下： 连续抛掷两枚均匀的硬币，如果两枚正面朝上，则小明获胜；如果两枚反面朝上，则小颖获胜；如果一枚正面朝上、一枚反面朝上，小凡获胜 . 小明 小颖 小凡 导入新课 用树状图或表格求概率 一 问题 1 ： 你认为上面游戏公平吗？ 活动探究： （ 1 ）每人抛掷硬币 20 次，并记录每次试验的结果，根据记录填写下面的表格： 抛掷的结果 两枚正面朝上 两枚反面朝上 一枚正面朝上，一枚反面朝上 频数 频率 讲授新课 （ 2 ）由上面的数据，请你分别估计“两枚正面朝上”“两枚反面朝上”“一枚正面朝上、一枚反面朝上”这三个事件的概率 . 问题 2 ： 通过实验数据 , 你认为该游戏公平吗？ 从上面的试验中我们发现，试验次数较大时，试验频率基本稳定，而且在一般情况下，“一枚正面朝上 . 一枚反面朝上”发生的概率大于其他两个事件发生的概率 . 所以，这个游戏不公平，它对小凡比较有利 . 议一议： 在上面抛掷硬币试验中， （ 1 ）抛掷第一枚硬币可能出现哪些结果？它们发生的可能性是否一样？ （ 2 ）抛掷第二枚硬币可能出现哪些结果？它们发生的可能性是否一样？ （ 3 ）在第一枚硬币正面朝上的情况下，第二枚硬币可能出现哪些结果？它们发生可能性是否一样？如果第一枚硬币反面朝上呢？ 由于硬币质地是均匀的，因此抛掷第一枚硬币出现 “ 正面朝上 ” 和 “ 反面朝上 ” 的概率相同 . 无论抛掷第一枚硬币出现怎样的结果，抛掷第二枚硬币时出现 “ 正面朝上 ” 和 “ 反面朝上 ” 的概率也是相同的 . 我们可以用树状图或表格表示所有可能出现的结果 . 开始 正 正 第一枚硬币 第二枚硬币 所有可能出现的结果 树状图 反 （正，正） （正，反） 反 正 反 （反，正） （反，反） 表格 正 反 正 反 第一枚硬币 第二枚硬币 （正，正） （反，正） （正，反） （反，反） 总共有 4 中结果 , 每种结果出现的可能性相同 . 其中： 小明获胜的概率： 小颖获胜的概率： 小凡获胜的概率： 利树状图或表格，我们可以不重复、不遗漏地列出所有可能性相同的结果，从而比较方便地求出某些事件发生的概率 . 结论 例 1 ： 小 颖有两件上衣，分别红色和白色，有两条裤子，分别为黑色和白色，她随机拿出一件上衣和一条裤子穿上，恰好是白色上衣和白色裤子的概率是多少？ 解析： 可采用画树状图或列表法把所有的情况都列举出来 . 解： 解法一 : 画树状图如图所示： 开始 白色 红色 黑色 白色 黑色 白色 上衣 裤子 由图中可知共有 4 种等可能结果，而白衣、黑裤只有 1 种可能， 概率为 . 解法二 : 将可能出现的结果列表如下： 黑色 白色 白色 （白，黑） （白，白） 红色 （红，黑） （红，白） 上衣 裤子 由图中可知共有 4 种等可能结果，而白衣、黑裤只有 1 种可能，概率为 . 例 2 ： 小可、子宣、欣怡三人在一起做游戏时，需要确定做游戏的先后顺序，她们约定用 “ 石头、剪刀、布 ” 的方式确定，那么在一个回合中，三个人都出 “ 石头 ” 的概率是多少？ 解： 用树状图分析所有可能的结果，如图： 开始 石头 剪刀 布 石头 剪刀 布 石头 剪刀 布 石头 剪刀 布 石头 剪刀 布 石头 剪刀 布 石头 剪刀 布 石头 剪刀 布 石头 剪刀 布 ...... ...... ...... ...... 由树状图可知所有等可能的结果有 27 种，三人都出“石头”的结果只有 1 种，所以在一个回合中三个人都出“石头”的概率为 . 当一次试验涉及三个或更多的因素时，为了不重不漏地列出所有可能的结果，通常采用树状图 . 归纳 画树状图求概率的基本步骤 方法归纳 （ 1 ） 明确一次试验的几个步骤及顺序； （ 2 ） 画树状图列举一次试验的所有可能结果； （ 3 ） 数出随机事件 A 包含的结果数 m ，试验的所有可能结果数 n ； （ 4 ） 用概率公式进行计算 . 列表法求概率应注意的问题 方法归纳 确保试验中每种结果出现的可能性大小相等 . 第一步：列表格； 第二步：在所有可能情况 n 中 , 再找到满足条件的事件的个数 m ； 第三步：代入概率公式 计算事件的概率 . 列表法求概率的基本步骤 一只箱子里共有 3 个球，其中有 2 个白球， 1 个红球，它们除了颜色外均相同 . （ 1 ）从箱子中任意摸出一个球，不将它放回箱子，搅匀后再摸出一个球，求两次摸出的球都是白球的概率； 1 2 白 1 白 2 红 白 1 —— （白 2 , 白 1 ） ( 红 , 白 1 ) 白 2 （白 1 , 白 2 ） —— （红 , 白 2 ） 红 （白 1 , 红） （白 2 ， 红） —— 解： （ 1 ）列表如下： 第二次 第一次 拓展延伸 （ 2 ）从箱子中任意摸出一个球，将它放回箱子，搅匀后再摸出一个球，求两次摸出的球都是白球的概率 . 1 2 白 1 白 2 红 白 1 （白 1 , 白 1 ） （白 2 , 白 1 ） ( 红 , 白 1 ) 白 2 （白 1 , 白 2 ） ( 白 2 , 白 2 ) （红 , 白 2 ） 红 （白 1 , 红） （白 2 ， 红） ( 红 , 红 ) 第二次 第一次 （ 1 ）当小球取出后不放入箱子时 , 共有 6 种结果，每个结果的可能性相同，摸出两个白球概率为： （ 2 ）小球取出后放入是，共有 9 种 结果 , 每种结果的可能性相同，摸出两个白球概率为： 1. 一个袋中有 2 个红球， 2 个黄球，每个球除颜色外都相同，从中一次摸出 2 个球， 2 个球都是红球的可能性是（　　） A. B. C. D. 2. 在一个不透明的袋 中装有 2 个黄球和 2 个红球 , 它们除颜色外没有其他区别 , 从袋中任意摸出一个球 , 然后放回搅匀 , 再从袋中任意摸一个球 , 那么两次都摸到黄球的概率是 ( ) A. B. C. D. D C 当堂练习 3. 如果有两组牌，它们的牌面数字分别是 1 ， 2 ， 3, 那么从每组牌中各摸出一张牌 . （ 1 ）摸出两张牌的数字之和为 4 的概念为多少？ （ 2 ）摸出为两张牌的数字相等的概率为多少？ 3 2 （ 2,3 ） （ 3,3 ） （ 3,2 ） （ 3,1 ） （ 2,2 ） （ 2,1 ） （ 1,3 ） （ 1,2 ） （ 1,1 ） 1 3 2 1 第二张牌 的牌面数字 第一张牌的 　牌面数字 解： （ 1 ） P （ 数字之和为 4 ） = . （ 2 ） P （ 数字相等 ） = 4. 在一个不透明的盒子里，装有三个分别写有数字 6 ， -2 ， 7 的小球，它们的形状、大小、质地等完全相同 . 先从盒子里随机取出一个小球，记下数字后 放回盒子 里，摇匀后再随机取出一个小球，记下数字 . 请你用列表或画树状图的方法求下列事件的概率 . （ 1 ）两次取出的小球上的数字相同； （ 2 ）两次取出的小球上的数字之和大于 10 . (1) 两次取出的小球上的数字相同的可能性只有3种，所以 P (数字相同)= (2) 两次取出的小球上的数字之和大于 10 的可能性只有 4 种，所以 P (数字之和大于10)= 解：根据题意，画出树状图如下 第一个数字 第二个数字 6 6 -2 7 -2 6 -2 7 7 6 -2 7 列举法 关键 常用 方法 直接列举法 列表法 画树状图法 适用对象 两个试验因素或分两步进行的试验 . 基本步骤 列表； 确定 m 、 n 值 代入概率公式计算 . 在于正确列举出试验结果的各种可能性 . 确保试验中每种结果出现的可能性大小相等 . 前提条件 课堂小结 树状图 步骤 用法 是一种解决试验有多步（或涉及多个因素）的好方法 . 注意 弄清试验涉及 试验因素个数 或 试验步骤分几步 ； 在摸球试验一定要弄清 “ 放回 ” 还是“ 不放回 ” . 关键要弄清楚每一步有几种结果； 在树状图下面对应写着所有可能的结果； 利用概率公式进行计算 .