- 2021-06-08 发布 |
- 37.5 KB |
- 43页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020春五年级数学下册六圆圆的认识课件(苏教版)
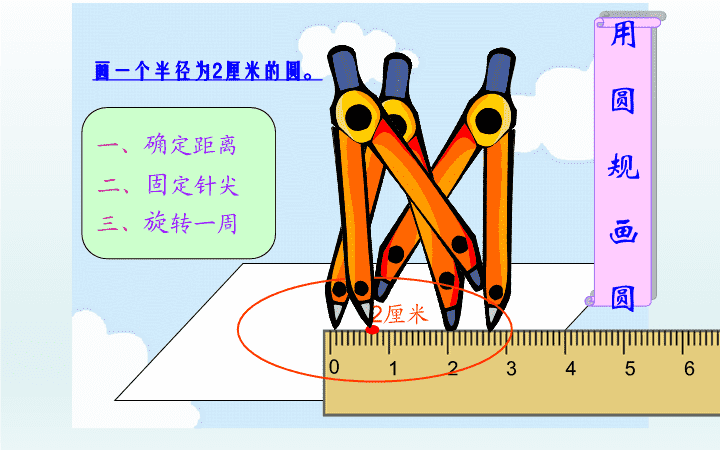
圆 圆的大小由 圆规两脚间的距离 决定。 2 厘米 圆的位置由 针尖的位置 决定 0 1 2 3 4 6 7 8 5 画一个半径为 2 厘米的圆。 一、 确 定距离 二、 固 定针尖 三、 旋 转一周 2 厘米 用 圆 规 画 圆 两脚之间的距离为2厘米 2 cm 长方形 正方形 平行四边形 梯形 三角形 圆 由 线段 围成的 平面 图形 圆是 曲线 围成的 平面 图形。 圆外 圆上 圆内 认识圆 圆心 O 圆心——用字母 O 表示 圆心决定圆的位置 连接 圆心和圆上任意一点 的线段叫做 半径 。 r 半径 圆心 O 半径 —— 用字母 r 表示 半径的长度决定圆的大小 判断:哪条是圆的半径? 1 号 3 号 4 号 2 号 不是半径。 因为它的 另一端不在 圆上 。 是半径。因为 它是连接圆心 到圆上一点 的线段。 直径 d 通过圆心 并且 两端都在圆上 的 线段 叫做 直径 。 直径 用字母 d 表示 在自己画的圆里标出 圆心 ,画一条 半径 和一条 直径 ,并分别用字母表示。 判断:哪条是圆的直径? 1 号 3 号 4 号 2 号 不是直径。 因为它的 另一端不在 圆上 不是直径。 因为没有 经过圆心。 不是直径。 因为它两端 都 不在 圆上。 是直径。因为 它经过圆心 并且两端 都在圆上。 o C D G H M N B F E 请说出下面图中 哪些是半径? 哪些不是,为什么? 哪些是直径? o 分别指出下面各圆的半径和直径,并量出它们的长度。 d d=2 厘米 r r=1 厘米 o • 在同一个圆里,有( )条半径, 它们的长度都( ) 无数 相等 半径的特征: 在同一个圆里,有( )条直径, 它们的长度都( ) 无数 相等 o • d r r d = r + r d=2r r= 在同一个圆里,直径是半径的 2倍 ,半径是直径的 一半 。 半径与直径的关系 : 2 1 d · O · O 等圆的半径相等,直径相等 在相等的圆里,直径是半径的 2倍 ,半径是直径的 一半 。 圆是轴对称图形,它有无数条对称轴。 o 对称轴是直径所在的直线。 圆的特征: 填写下表。 0.24 米 6 米 直径 ( d ) 3.9 米 7 厘米 20 厘米 半径 ( r ) 40 厘米 3 米 14 厘米 0.12 米 7.8 米 1. 两端都在圆上的 线段叫做直径。 ( ) 2. 在两个等圆里,所有的半径都相等。 ( ) 3. 半径是直径的一半。( ) 4. 半径 2 厘米的圆比直径 3 厘米的圆大。 ( ) 分析 : 通过圆心,并且 分析 : 在同圆或等圆中 分析 : 直径等于 4 厘米 × × √ √ ( 1 )画圆时,圆规两脚间的距离是( )。 A. 半径长度 B. 直径长度 ( 2 )从圆心到 ( ) 任意一点的线段 , 叫半径。 A. 圆心 B. 圆外 C. 圆上 ( 3 )通过圆心并且两端都在圆上的 ( ) 叫直径。 A. 直径 B. 线段 C. 射线 A C B 我国是世界上最早研究圆的国家,早在2000多年前,我国的墨子作出了圆的概念: “ 圆, 一中同长也 ” 。 这个定义比希腊数学家欧几里得给圆下定义要早1000多年 。 墨子 圆心到圆上任意一点的距离都 相等 。 ( 1 )半径是射线,直径是直线。 ( ) 对的打“√” 错的打“ ×” × ( 4 ) 画一个直径 4 厘米的圆,圆规两脚的距离应该是 4 厘米。 ( ) ( 2 )直径长度是半径的 2 倍。 ( ) ( 3 )圆心决定圆的位置,半径决定圆的大小。 ( ) √ × 分析 : 在同圆或等圆中 × 分析 : 圆规两脚间的距离是半径 圆心( O) 直径( d) 半径( r) 画出美 丽的圆 在同一个圆里,直径是半径的2倍,半径是直径的一半. 画圆时,针尖固定的一点叫做圆心 。 连接圆心和圆上任意 一点的线段叫做半径 通过圆心并且两端 都在圆上的线段叫做直径 在同一个圆里,有无数 条直径,它们的长度都相等 在同一个圆里,有无数条 半径,它们的长度都相等 d O r 圆 的 周 长 方法一: 绳绕法 怎样才能知道一个圆的周长? 方法一: 绳绕法 其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做 圆周率 ,用字母 “ π (读pài) ” 表示。他是一个无限不循环小数, π= 3.1415926535 …… 但在实际应用中一般只取它的 近似值 , 即 π≈3.14 。 实际上, π>3.14 圆的周长和什么有关? o o r r 让我们来做一个实验,找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中。看看你有什么发现。 物品名称 周长 (厘米) 直径 (厘米) (保留两位小数) 一角硬币 手镯 五角硬币 一元硬币 7.8 6.3 22 2 2.5 7 1.9 5.9 3.10 3.15 3.14 3.13 你发现圆的周长和直径之间有什么关系? 一个圆的周长总是它的直径的 3 倍多一些。 祖冲之 约 1500 年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在 3.1415926 和 3.1415927 之间,成为世界上第一个把圆周率的值的计算精确到 7 位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早一千年。 C = π d C = 2 π r 圆的周长 = 直径 × 圆周率 d= C π r = C 2π 圆的周长÷圆的直径=圆周率 C ÷ d = π 求出下列各圆的周长 d=2 厘米 r=2 厘米 3.14×2 = 6.28 ( 厘米 ) 2×3.14×2 = 6.28×2 = 12.56 ( 厘米 ) 一个圆形喷水池的半径是 5m ,它的周长是多少米? 2× 3.14×5 =3.14 ×10 =31.4 ( m ) 答:它的周长是 31.4 米。 我的收获 ( 1 )今天我学习了圆周长的知识。我知道圆周率是( )和( )的比值,它用字母( )表示 , 它是我国古代数学家( )发现的。 直径 d Π ≈ 3.14 周长 直径 祖冲之 ( 2 )我还知道圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。 π C = d π C = r 2 π π 圆 的 面 积 面积是什么? 物体的表面或平面图形的大小,叫做面积。 常用的面积单位有: 平方厘米 、 平方分米 和 平方米 。 圆 所占平面的大小,叫做 圆的面积 。 S = πr 2 圆的面积计算公式: 知道哪些条件就可以求圆的面积? 已知 半径、直径 或是 周长 都可以求圆的面积 一个圆的半径是 4 厘米。它的面积是多少平方厘米? 4 米 S = πr 2 =3.14×4 2 = 3.14 × 16 = 50.24 ( 平方厘米 ) 答:它的面积是50.24平方厘米。 先算4的平方 圆 的 面 积 1 、圆的面积:圆所占平面的大小 2 、圆面积的计算公式: S = πr 2 3 、已知圆的半径、直径和周长都可以求出圆的面积。 4 、环形的面积计算公式: π R 2 - π r 2 或 π (R 2 - r 2 ) 《 圆 的 面 积 》查看更多