2016年高考真题——数学（江苏卷） 原卷版

2016年高考真题——数学（江苏卷） 原卷版

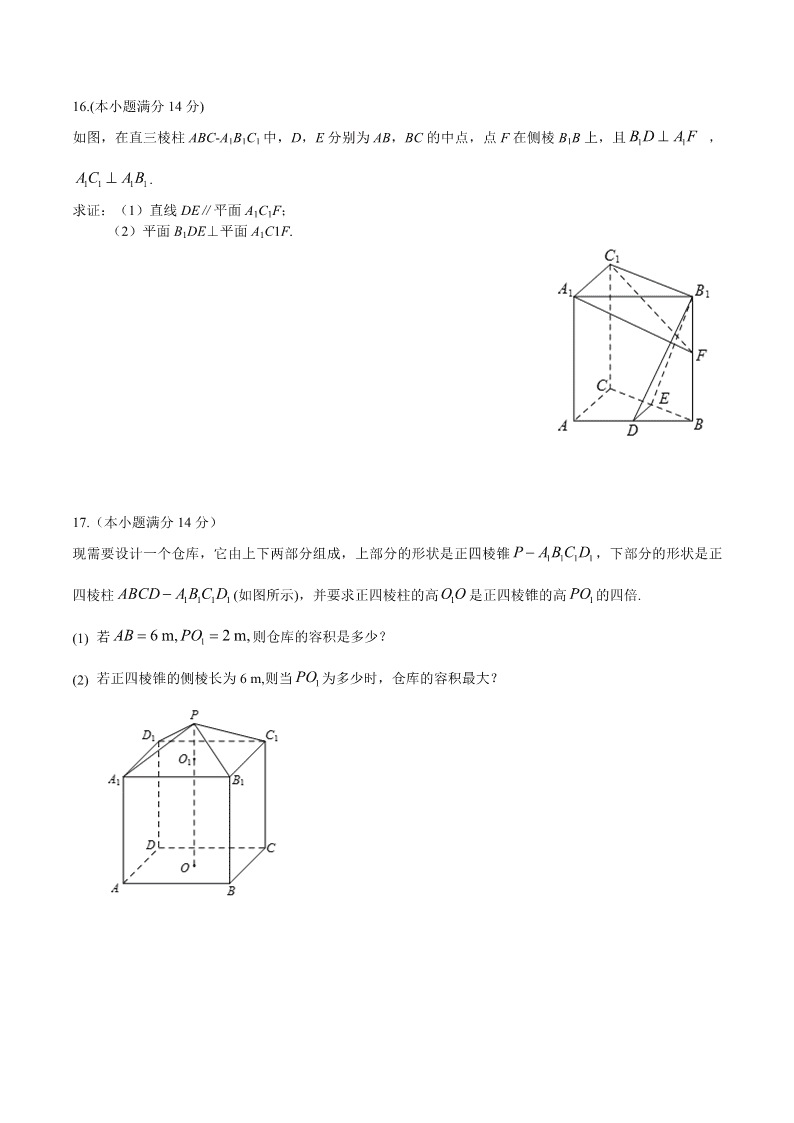
2016 年普通高等学校招生全国统一考试（江苏卷） 数学Ⅰ 参考公式 圆柱的体积公式： =Sh，其中 S 是圆柱的底面积，h 为高. 圆锥的体积公式： Sh，其中 S 是圆锥的底面积，h 为高. 一、填空题：本大题共 14 个小题,每小题 5 分,共 70 分.请把答案写在答题卡相应位置上。 1.已知集合 则 ________▲________. 2.复数 其中 i 为虚数单位，则 z 的实部是________▲________. 3.在平面直角坐标系 xOy 中，双曲线 的焦距是________▲________. 4.已知一组数据 4.7,4.8,5.1,5.4,5.5，则该组数据的方差是________▲________. 5.函数 y= 的定义域是 ▲ . 6.如图是一个算法的流程图，则输出的 a 的值是 ▲ . 7.将一颗质地均匀的骰子（一种各个面上分别标有 1，2，3，4，5，6 个点的正方体玩具）先后抛掷 2 次， 则出现向上的点数之和小于 10 的概率是 ▲ . 8.已知{an}是等差数列，Sn 是其前 n 项和.若 a1+a22= 3，S5=10，则 a9 的值是 ▲ . 9.定义在区间[0,3π]上的函数 y=sin2x 的图象与 y=cosx 的图象的交点个数是 ▲ . 10.如图，在平面直角坐标系 xOy 中，F 是椭圆 的右焦点，直线 与椭圆交于 B，C 两点，且 ,则该椭圆的离心率是 ▲ . V圆柱 V圆锥 1 3 { 1,2,3,6}, { | 2 3},A B x x      =A B (1 2i)(3 i),z    2 2 17 3 x y  23 2x x- - 开始 输出a 结束 1a 9b a b 4a a  2b b  Y N - 2 2 2 2 1( )x y a ba b  ＞ ＞0 2 by  90BFC   (第 10 题) 11.设 f（x）是定义在 R 上且周期为 2 的函数，在区间[ −1,1)上， 其中 若 ，则 f（5a）的值是 ▲ . 12. 已知实数 x，y 满足 ，则 x2+y2 的取值范围是 ▲ . 13.如图，在△ABC 中，D 是 BC 的中点，E，F 是 AD 上的两个三等分点， ， ， 则 的值是 ▲ . 14.在锐角三角形 ABC 中，若 sinA=2sinBsinC，则 tanAtanBtanC 的最小值是 ▲ . 二、解答题 （本大题共 6 小题，共 90 分.请在答题卡制定区域内作答，解答时应写出文字说明、证明过程 或演算步骤.） 15.（本小题满分 14 分） 在 中，AC=6， （1）求 AB 的长； （2）求 的值. F CB O y x , 1 0, ( ) 2 ,0 1,5 x a x f x x x          .aR 5 9( ) ( )2 2f f  2 4 0 2 2 0 3 3 0 x y x y x y            4BC CA   1BF CF    BE CE  ABC△ 4 πcos .5 4B C= =， πcos( 6A- ) F E D CB A 16.(本小题满分 14 分) 如图，在直三棱柱 ABC-A1B1C1 中，D，E 分别为 AB，BC 的中点，点 F 在侧棱 B1B 上，且 ， . 求证：（1）直线 DE∥平面 A1C1F； （2）平面 B1DE⊥平面 A1C1F. 17.（本小题满分 14 分） 现需要设计一个仓库，它由上下两部分组成，上部分的形状是正四棱锥 ，下部分的形状是正 四棱柱 (如图所示)，并要求正四棱柱的高 是正四棱锥的高 的四倍. (1) 若 则仓库的容积是多少？ (2) 若正四棱锥的侧棱长为 6 m,则当 为多少时，仓库的容积最大？ 1 1B D A F 1 1 1 1AC A B 1 1 1 1P A B C D 1 1 1 1ABCD A B C D 1O O 1PO 16 m, 2 m,AB PO  1PO 18. （本小题满分 16 分） 如图，在平面直角坐标系 xOy 中，已知以 M 为圆心的圆 M: 及其上一点 A(2，4) (1) 设圆 N 与 x 轴相切，与圆 M 外切，且圆心 N 在直线 x=6 上，求圆 N 的标准方程； (2) 设平行于 OA 的直线 l 与圆 M 相交于 B、C 两点，且 BC=OA,求直线 l 的方程； (3) 设点 T（t,0）满足：存在圆 M 上的两点 P 和 Q,使得 ,求实数 t 的取值范围。 19. （本小题满分 16 分） 已知函数 . （1） 设 a=2,b= . ① 求方程 =2 的根; ②若对任意 ,不等式 恒成立，求实数 m 的最大值； （2）若 ，函数 有且只有 1 个零点，求 ab 的值. 20.（本小题满分 16 分） 记 .对数列 和 的子集 T，若 ,定义 ;若 ， 定义 .例如： 时， .现设 是公比为 3 的等比 数列，且当 时， . (1) 求数列 的通项公式； (2) 对任意正整数 ，若 ，求证： ； (3) 设 ,求证： . 2 2 12 14 60 0x y x y     ,TA TP TQ    ( ) ( 0, 0, 1, 1)x xf x a b a b a b      1 2 ( )f x x R (2 ) f( ) 6f x m x  0 1, 1a b  ＞     2g x f x   1,2, 100U  … ，   * na n N U T   0TS   1 2, , kT t t t … ， 1 2 + kT t t tS a a a  …  = 1,3,66T 1 3 66+TS a a a    * na n N  = 2,4T =30TS  na  1 100k k   1,2, kT  … ， 1T kS a  , , C DC U D U S S   2C C D DS S S  数学Ⅱ（附加题） 21.【选做题】本题包括 A、B、C、D 四小题，请选定其中两小题，并在相应的答题区域内作答．若多做， 则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤． A．【选修 4—1 几何证明选讲】（本小题满分 10 分） 如图，在△ABC 中，∠ABC=90°，BD⊥AC，D 为垂足，E 是 BC 的中点，求证：∠EDC=∠ABD. B.【选修 4—2：矩阵与变换】（本小题满分 10 分） 已知矩阵 矩阵 B 的逆矩阵 ，求矩阵 AB. C.【选修 4—4：坐标系与参数方程】（本小题满分 10 分） 在平面直角坐标系 xOy 中，已知直线 l 的参数方程为 （t 为参数），椭圆 C 的参数方程 为 （ 为参数）.设直线 l 与椭圆 C 相交于 A，B 两点，求线段 AB 的长. D.设 a＞0，|x-1|＜ ，|y-2|＜ ，求证：|2x+y-4|＜a. 【必做题】第 22 题、第 23 题，每题 10 分，共计 20 分. 请在答题卡指定区域内作答．解答时应写出文字说 明、证明过程或演算步骤． 1 2 ,0 2A      1 11= 2 0 2 B        11 2 3 2 x t y t      cos , 2sin x y       3 a 3 a 22. （本小题满分 10 分） 如图，在平面直角坐标系 xOy 中，已知直线 l：x-y-2=0，抛物线 C：y2=2px(p＞0). （1）若直线 l 过抛物线 C 的焦点，求抛物线 C 的方程； （2）已知抛物线 C 上存在关于直线 l 对称的相异两点 P 和 Q. ①求证：线段 PQ 的中点坐标为（2-p，-p）； ② 求 p 的取值范围. 23.（本小题满分 10 分） （1）求 的值； （2）设 m，n N*，n≥m，求证： （m+1） +（m+2） +（m+3） +…+n +（n+1） =（m+1） . 参考答案 3 4 6 7–47C C  Cm m +1Cm m +2Cm m –1Cm n Cm n +2 +2Cm n 1. 2.5 3. 4.0.1 5. 6.9 7. 8.20. 9.7. 10. 11. 12. 13. 14.8. 15.解（1）因为 所以 由正弦定理知 ，所以 （2）在三角形 ABC 中 ，所以 于是 又 ，故 因为 ，所以 因此 16.证明：（1）在直三棱柱 中， 在三角形 ABC 中，因为 D,E 分别为 AB,BC 的中点. 所以 ，于是  1,2 2 10  3,1 5.6 6 3 2 5 4[ ,13]5 7 8 4cos ,0 ,5B B    2 24 3sin 1 cos 1 ( ) ,5 5B B     sin sin AC AB B C 26sin 2 5 2.3sin 5 AC CAB B    A B C    ( ).A B C   cosA cos(B C) cos( ) cos cos sin sin ,4 4 4B B B           4 3cos ,sin ,5 5B B  4 2 3 2 2cos 5 2 5 2 10A        0 A   2 7 2sin 1 cos 10A A   2 3 7 2 1 7 2 6cos( ) cos cos sin sin .6 6 6 10 2 10 2 20A A A            1 1 1ABC A B C 1 1/ /AC AC / /DE AC 1 1/ /DE AC 又因为 DE 平面 平面 所以直线 DE//平面 （2）在直三棱柱 中， 因为 平面 ，所以 又因为 所以 平面 因为 平面 ，所以 又因为 所以 因为直线 ，所以 17.本小题主要考查函数的概念、导数的应用、棱柱和棱锥的体积等基础知识，考查空间想象能力和运用数 学模型及数学知识分析和解决实际问题的能力.满分 14 分. 解：（1）由 PO1=2 知 OO1=4PO1=8. 因为 A1B1=AB=6， 所以正四棱锥 P-A1B1C1D1 的体积 正四棱柱 ABCD-A1B1C1D1 的体积 所以仓库的容积 V=V 锥+V 柱=24+288=312（m3）. (2)设 A1B1=a(m),PO1=h(m)，则 0

查看更多