2020学年高一数学下学期第一次月考试题（实验班）

2020学年高一数学下学期第一次月考试题（实验班）

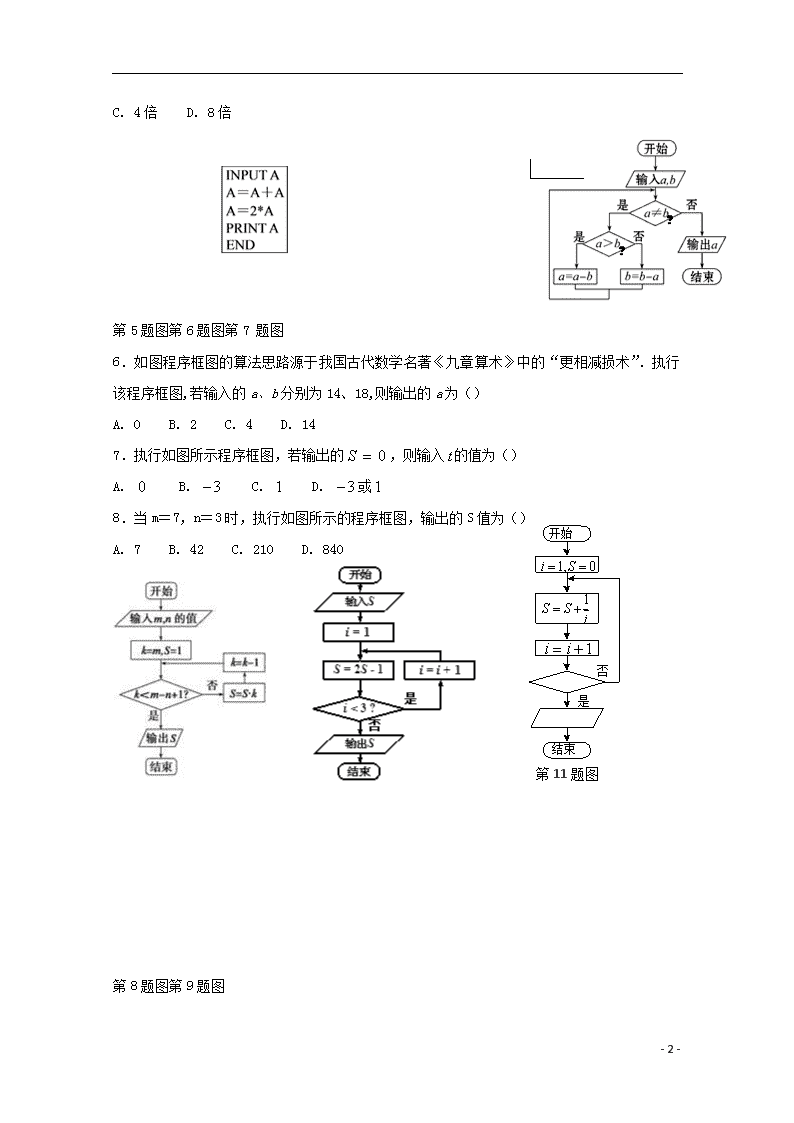
‎2019学年高一数学下学期第一次月考试题（实验班）‎ 第Ⅰ卷（共60分）2019-4-5‎ 一、选择题：本大题共12个小题,每小题5分,共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．现要完成下列3项抽样调查：‎ ‎①从10盒酸奶中抽取3盒进行食品卫生检查．‎ ‎②科技报告厅有32排，每排有40个座位，有一次报告会恰好坐满了听众，报告会结束后，为了听取意见，需要请32名听众进行座谈．‎ ‎③某中学共有160名教职工，其中一般教师120名，行政人员16名，后勤人员24名．为了了解教职工对学校在校务公开方面的意见，拟抽取一个容量为20的样本．‎ 较为合理的抽样方法是()‎ A．①简单随机抽样，②系统抽样，③分层抽样B．①简单随机抽样，②分层抽样，③系统抽样 C．①系统抽样，②简单随机抽样，③分层抽样D．①分层抽样，②系统抽样，③简单随机抽样 ‎2.总体编号为01,02,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为（　　） ‎ A．07 B．02 C．01 D．04‎ ‎3．如上右图，面积为4的矩形ABCD内一块阴影部分，若往矩形ABCD内随机投掷1000个点，‎ 落在矩形的非阴影部分中的点数为600个，则据此估计阴影部分的面积为（）‎ A．B． C．D．‎ ‎4．小李从网上购买了一件商品，快递员计划在5:00-6:00之间送货上门.已知小李下班到家的时间为下午5:30-6:00.快递员到小李家时，如果小李未到家，就将商品存放到快递柜中，则小李需要去快递柜收取商品的概率等于（）‎ A． B． C. D．‎ ‎5．以下程序中，输出时A的值是输入时A的值的 (　 　)‎ A. 2倍 B. 3倍 - 13 -‎ C. 4倍 D. 8倍 第5题图第6题图第7 题图 ‎6．如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图,若输入的a、b分别为14、18,则输出的a为（）　‎ A. 0 B. 2 C. 4 D. 14‎ ‎7．执行如图所示程序框图，若输出的，则输入的值为（）‎ A. B. C. D. 或 是 否 开始 结束 第11题图 ‎8．当m＝7，n＝3时，执行如图所示的程序框图，输出的S值为（）‎ A. 7 B. 42 C. 210 D. 840‎ 第8题图第9题图 - 13 -‎ ‎9．《算法统宗》是中国古代数学名著，由明代数学家程大位所著，该作完善了珠算口诀，确立了算盘用法，完成了由筹算到珠算的彻底转变，该作中有题为“李白沽酒”“李白街上走，提壶去买酒。遇店加一倍，见花喝一斗,三遇店和花，喝光壶中酒。借问此壶中，原有多少酒？”，如图为该问题的程序框图，若输出的值为0，则开始输入的值为( )‎ A. B. C. D. ‎ ‎10．为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为，众数为,平均值为,则(　　)‎ A. B. ‎ C. D.‎ ‎11.右面程序框图是为了求出满足的最大正整数n的值，‎ 那么在 和 两个空白框中，可以分别填入（）‎ ‎（A）“”和“输出”（B）“”和“输出”‎ ‎（C）“”和“输出”（D)“”和“输出”‎ ‎12．在发生某公共卫生事件期间，有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”．根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是()‎ A．甲地：总体均值为3，中位数为4B．乙地：总体均值为1，总体方差大于0‎ C．丙地：中位数为2，众数为3D．丁地：总体均值为2，总体方差为3‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．有20位同学，编号从1至20，现在用系统抽样方法从中抽取4人作问卷调查，已知抽到的样本中有一个编号为3，请写出另外的三个编号____________‎ - 13 -‎ ‎14．用红、黄、蓝三种不同颜色给图中3个矩形随机涂色，每个矩形只涂一种颜色，则这3个矩形颜色都不同的概率是___________．‎ ‎15．某数学老师身高176 cm，他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm.因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为________ cm.（线性回归分析相关公式见解答题）‎ ‎16.天气预报说，在今后的三天中，每一天下雨的概率均为60%，某同学利用随机模拟的方法求解事件A：“这三天中恰有两天下雨”的概率，方法如下，①利用随机数表产生40组随机数；②利用0,1,2,3,4,5表示下雨，6,7,8,9,表示不下雨；③估计A发生的概率。‎ 如果该同学从随机数表的第6行第1列开始读起，那么他估计A发生的概率应该是_________‎ 附：随机数表（第6行到第9行）‎ ‎16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64‎ ‎84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76‎ ‎63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79‎ ‎33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54‎ 三、解答题（本大题共6小题，共70分．其中第17题10分，其余各题为12分。‎ 解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．某城市100户居民的月平均用电量(单位:度),‎ 以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.‎ ‎(1)求直方图中x的值;‎ ‎(2)求月平均用电量的众数和中位数;‎ ‎(3)在月平均用电量为[220,240),[240,260),[260,280),‎ 的三组用户中,用分层抽样的方法抽取10户居民,‎ 则月平均用电量在[220,240)的用户中应抽取多少户?‎ - 13 -‎ ‎18. 某班级甲、乙两个小组各有10位同学，在一次期中考试中，两个小组同学的数学成绩如下：‎ 甲组：94,69,73,86,74,75,86,88,97,98；‎ 乙组：75,92,82,80,95,81,83,91,79,82.‎ ‎（1）画出这两个小组同学数学成绩的茎叶图，判断哪一个小组同学的数学成绩差异较大（直接给出结论）；‎ ‎（2）从这两个小组数学成绩在90分以上的同学中，随机选取2人在全班介绍学习经验，求选出的2位同学不在同一个小组的概率.‎ ‎19．某厂为检验车间一生产线是否工作正常，现从生产线中随机抽取一批零件样本，测量尺寸（单位：）绘成频率分布直方图如图所示：‎ ‎（Ⅰ）求该批零件样本尺寸的平均数和样本方差（同一组中的数据用该组区间的中点值作代表）；‎ - 13 -‎ ‎（Ⅱ）已知该批零件尺寸服从正态分布，其中近似为样本平均数，近似为样本方差，若从生产线中任取一零件，测量尺寸为，根据原则判断该生产线是否正常？‎ 附：，，‎ ‎20.已知药用昆虫的产卵数与一定范围内的温度有关，现收集了该中药用昆虫的6组观测数据如表：‎ 温度/℃‎ ‎21‎ ‎23‎ ‎24‎ ‎27‎ ‎29‎ ‎32‎ 产卵数/个 ‎6‎ ‎11‎ ‎20‎ ‎27‎ ‎57‎ ‎77‎ 经计算得：，线性回归模型的残差平方和为，分别为观察数据中温度和产卵数，‎ ‎（1）若用线性回归模型，求关于的回归方程（精确到）；‎ ‎（2）若用非线性回归模型求得关于的回归方程，且相关指数，试与（1）中的回归模型相比.‎ ‎①统计学上认为相关指数越接近1，回归模型的拟合效果越好，请用说明哪种模型的拟合效果更好；‎ ‎②用拟合效果更好的模型预测温度为时该中药用昆虫的产卵数（结果取整数）.‎ 附：一组数据，其回归直线 - 13 -‎ 的斜率和截距的最小二乘估计分为，相关指数 ‎21．已知某池塘养殖着鲤鱼和鲫鱼,为了估计这两种鱼的数量,养殖者从池塘中捕出这两种鱼各1 000条,给每条鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机地捕出1 000条鱼,记录下其中有记号的鱼的数目,立即放回池塘中.这样的记录做了10次,并将记录获取的数据制作成如图所示的茎叶图.‎ ‎(1)根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数,并估计池塘中的鲤鱼和鲫鱼的数量;‎ ‎(2)为了估计池塘中鱼的总质量,现按照(1)中的比例从池塘中抽取100条鱼并进行称重,根据称重鱼的质量介于[0,4.5](单位:千克)之间,将测量结果按如下方式分成九组:第一组[0,0.5),第二组[0.5,1),…,第九组[4,4.5].如图是按上述分组方法得到的频率分布直方图的一部分.‎ ‎①估计池塘中鱼的质量在3千克以上(含3千克)的条数;‎ ‎②若第三组鱼的条数比第二组多7条、第四组鱼的条数比第三组多7条,请将频率分布直方图补充完整;‎ ‎③在②的条件下估计池塘中鱼的质量的众数及池塘中鱼的总质量.‎ - 13 -‎ ‎22．某工厂生产不同规格的一种产品，根据检测标准，其合格产品的质量与尺寸之间满足关系式为大于的常数），现随机抽取6件合格产品，测得数据如下：‎ 对数据作了处理，相关统计量的值如下表：‎ ‎（1）根据所给数据，求关于的回归方程（提示：是的线性关系）；‎ ‎（2）按照某项指标测定，当产品质量与尺寸的比在区间内时为优等品，现从抽取的6件合格产品再任选3件，求恰好取得两件优等品的概率；‎ ‎（附：对于一组数据，其回归直线的斜率和截距的最小二乘法估计值分别为）‎ - 13 -‎ 莆田第六中学2019学年高一下学期4月月考数学（A）‎ 参考答案 一、选择题 1-5：ACBAC 6-10：BDCCD 11-12：DD 二、填空题 ‎13. 8,13,18 14. 15. 185 16. 0.35‎ 三、解答题 ‎17．【解析】试题分析：‎ ‎(1)利用频率分布直方图小长方形的面积之和为1可得x＝0.0075；‎ ‎(2)结合所给的数据可得：月平均用电量的众数和中位数为,224;‎ ‎(3)结合频率分布直方图和分层抽样的概念可得月平均用电量在[220，240）的用户中应抽取5户.‎ 试题解析：‎ ‎（Ⅰ）由直方图的性质，可得 ‎（0.002＋0.0095＋0.011＋0.0125＋x＋0.005＋0.0025）×20＝1‎ 得：x＝0.0075，所以直方图中x的值是0.0075．．．．．．．．．．3分 ‎（Ⅱ）月平均用电量的众数是．‎ 因为（0.002＋0.0095＋0.011）×20＝0.45＜0.5，所以月平均用电量的中位数在[220，240）内，‎ 设中位数为a，由（0.002＋0.0095＋0.011）×20＋0.0125×（a－220）＝0.5，‎ 解得：a＝224，‎ 所以月平均用电量的中位数是224．．．．．．．．．．7分 ‎（Ⅲ）月平均用电量为[220，240]的用户有0.0125×20×100＝25（户），月平均用电量为[240，260）的用户有0.0075×20×100＝15（户），月平均用电量为[260，280）的用户有：‎ ‎0.005×20×100＝10（户），‎ 抽取比例，所以月平均用电量在[220，240）的用户中应抽取 - 13 -‎ （户）‎ ‎．．．．．．．．．．．．10分 ‎18.由茎叶图中数据分布可知，甲组数据分布比较分散，乙组数据分布相对集中，所以，甲组同学的成绩差异较大. ．．．．．．．．．3分 ‎（也可通过计算方差说明：，，）‎ ‎．．．．．．．．．6分 设甲组数据成绩在90分以上的三位同学为；.．．．．．．．．．7分 乙组数据在90分以上的三位同学为.．．．．．．．．．8分 从这6位同学中选出2位同学，共有15个基本事件，列举如下：‎ ‎，，，，；‎ ‎，，，；‎ ‎，，；‎ ‎，，..．．．．．．．．．10分 其中，从这6位同学中选出2位同学不在同一个小组共有9个基本事件，‎ ‎..．．．．．．．．．12分 ‎19．【解析】‎ ‎（Ⅰ） ..．．．．．．．．．3分 ‎ ；.．．．．．．．．．6分 - 13 -‎ ‎（Ⅱ）由（Ⅰ）知， ..．．．．．．．．．7分 ‎∵， ，‎ ‎∴..．．．．．．．．．9分 ‎∵，小概率事件发生了，.．．．．．．．．．10分 ‎∴该生产线工作不正常. .．．．．．．．．．12分 ‎20. .（1）依题意，，.．．．．．．．．．2分 所以，.．．．．．．．．．4分 所以关于的线性回归方程为。.．．．．．．．．．5分 ‎（2）①利用所给的数据 得线性回归方程为的相关指数 ‎，.．．．．．．．．．7分 因为，因此，回归模型比线性回归方程模型拟合效果更好；.．．．．．．．．．8分 ‎②由①的温度时，，.．．．．．．．．．10分 因为，所以个，‎ 所以当温度时，该种药用昆虫的产卵数估计为190个。‎ ‎．．．．．．．．．12分 ‎21．试题解析：‎ ‎(1)根据茎叶图可知,鲤鱼与鲫鱼的平均数目分别为80,20. .．．．．．．．．．2分 - 13 -‎ 由题意知,池塘中鱼的总数目为1 000÷=20 000(条), .．．．．．．．．．3分 则估计鲤鱼数目为20 000×=16 000(条),鲫鱼数目为20 000-16 000=4 000(条). .．．．．．．．．．4分 ‎(2)①根据题意,结合直方图可知,池塘中鱼的质量在3千克以上(含3千克)的条数约为20 000×(0.12+0.08+0.04)×0.5=2 400(条). .．．．．．．．．．6分 ‎②设第二组鱼的条数为x,则第三、四组鱼的条数分别为x+7,x+14,则有x+x+7+x+14=100×(1-0.55),解得x=8, .．．．．．．．．．8分 故第二、三、四组的频率分别为0.08,0.15,0.22,它们在频率分布直方图中的小矩形的高度分别为0.16,0.30,0.44,据此可将频率分布直方图补充完整(如图所示).‎ ‎.．．．．．．．．．10分 ‎③众数为2.25(千克),平均数为0.25×0.04+0.75×0.08+1.25×0.15+…+4.25×0.02=2.02(千克),所以鱼的总质量为2.02×20 000=40 400(千克).‎ ‎．．．．．．．．．12分 ‎22.（1）对，两边取自然对数得，.．．．．．．．．．1分 令，得，.．．．．．．．．．2分 - 13 -‎ ‎，.．．．．．．．．．4分 ‎ ，.．．．．．．．．．5分 得，故所求回归方程为..．．．．．．．．．6分 ‎（2）由，‎ 解得， ，即优等品有3件. .．．．．．．．．．8分 记“恰好取得两件优等品”为事件,‎ 从件合格品中选出3件的方法数为，.．．．．．．．．．10分（列举过程略）‎ 从件合格品取3件恰好2件为优等品的取法有种，.．．．．．．．．．11分 则..．．．．．．．．．12分 - 13 -‎