北京市通州区2020届高三上学期期末考试数学试题

北京市通州区2020届高三上学期期末考试数学试题

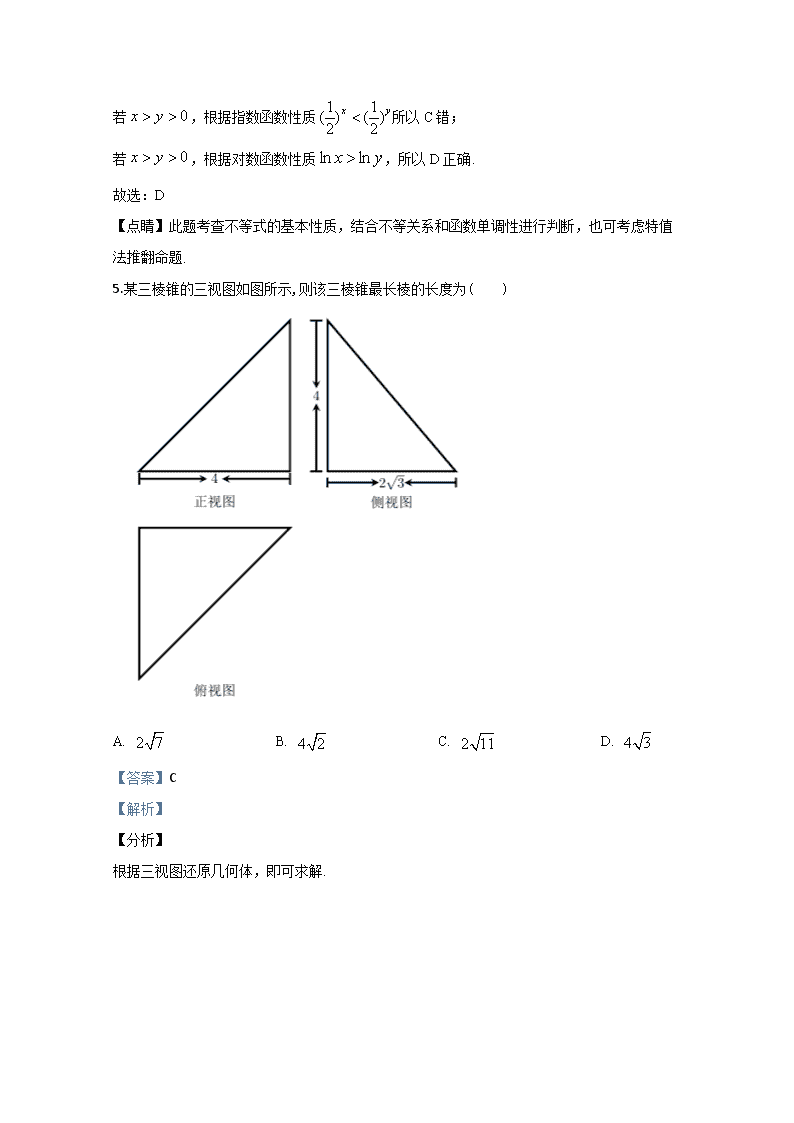
通州区2019-2020学年第一学期高三年级期末考试 数学试卷 第一部分(选择题 共40分)‎ 一､选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,只有一项是符合题目要求的.‎ ‎1.已知集合,,则( )‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据并集运算法则求解即可.‎ ‎【详解】由题：集合,,‎ 则.‎ 故选：A ‎【点睛】此题考查根据描述法表示的集合，并求两个集合的并集.‎ ‎2.在复平面内,复数(其中是虚数单位)对应的点位于( )‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 化简复数，得出其在复平面内的点，即可判定位置.‎ ‎【详解】由题：复数，‎ 在复平面内对应的点为，‎ 位于第一象限.‎ 故选：A ‎【点睛】此题考查复数的基本运算和复数对应复平面内的点的辨析，关键在于准确计算，熟练掌握几何意义.‎ ‎3.已知点A(2,a)为抛物线图象上一点,点F为抛物线的焦点,则等于( )‎ A. 4 B. ‎3 ‎C. D. 2‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 写出焦点坐标，根据抛物线上点到焦点距离公式即可求解.‎ ‎【详解】由题：点A(2,a)为抛物线图象上一点,‎ 点F为抛物线的焦点,所以，‎ 根据焦半径公式得：.‎ 故选：B ‎【点睛】此题考查求抛物线上的点到焦点的距离，结合几何意义根据焦半径公式求解即可.‎ ‎4.若,则下列各式中一定正确的是( )‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 若，，所以AC错；，所以B错；‎ 若，，所以D正确.‎ ‎【详解】由题：若，根据反比例函数性质，所以A错误；‎ 若，取，所以B错；‎ 若，根据指数函数性质所以C错；‎ 若，根据对数函数性质，所以D正确.‎ 故选：D ‎【点睛】此题考查不等式的基本性质，结合不等关系和函数单调性进行判断，也可考虑特值法推翻命题.‎ ‎5.某三棱锥的三视图如图所示,则该三棱锥最长棱的长度为( )‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据三视图还原几何体，即可求解.‎ ‎【详解】‎ 根据三视图还原几何体如图所示：其中，平面，‎ 由图可得：，所以，‎ ‎，‎ 所以最长的棱长.‎ 故选：C ‎【点睛】此题考查根据三视图还原几何体，计算几何体中的棱长，关键在于正确认识三视图，准确还原.‎ ‎6.甲､乙､丙､丁四名同学和一名老师站成一排合影留念.若老师站在正中间,甲同学不与老师相邻,乙同学与老师相邻,则不同站法种数为( )‎ A. 24 B. ‎12 ‎C. 8 D. 6‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据特殊元素优先考虑原则，先排乙，再排甲，结合左右对称原则求解.‎ ‎【详解】由题：老师站中间，‎ 第一步：排乙，乙与老师相邻，2种排法；‎ 第二步：排甲，此时甲有两个位置可以站，2种排法；‎ 第三步：排剩下两位同学，2种排法，‎ 所以共8种.‎ 故选：C ‎【点睛】此题考查计数原理，关键在于弄清计数方法，根据分步和分类计数原理解决实际问题.‎ ‎7.对于向量,, “”是“”的( )‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据向量的运算法则：“”不能推出“”， “”能够推出“”.‎ ‎【详解】当时，满足，不能推出，‎ 若，则，所以，‎ 所以“”是“”的必要不充分条件.‎ 故选：B ‎【点睛】此题考查充分条件与必要条件的关系判断，关键在于弄清向量间的关系，正确辨析即可.‎ ‎8.关于函数有以下三个判断 ‎①函数恒有两个零点且两个零点之积为-1；‎ ‎②函数恒有两个极值点且两个极值点之积为-1；‎ ‎③若是函数的一个极值点,则函数极小值为-1.‎ 其中正确判断的个数有( )‎ A. 0个 B. 1个 C. 个 D. 个 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 函数的零点个数即的根的个数，利用判别式求解；对函数求导讨论导函数的零点问题即可得极值关系.‎ ‎【详解】因为，方程，，所以关于的方程 一定有两个实根，且两根之积为-1，所以恒有两个零点且两个零点之积为-1，即①正确；‎ ‎，，对于，‎ ‎，所以恒有两个不等实根，且导函数在这两个实根附近左右异号，两根之积为，函数恒有两个极值点且两个极值点之积为，所以②错误；‎ 若是函数的一个极值点, ，则，‎ ‎，‎ ‎，‎ ‎，，‎ 所以函数的增区间为，减区间为，‎ 所以函数的极小值为，所以③正确.‎ 故选：C ‎【点睛】此题考查函数零点问题，利用导函数导论单调性和极值问题，综合性比较强.‎ 第二部分(非选择题 共110分)‎ 二､填空题:本大题共6小题,每小题5分,共30分.‎ ‎9.已知向量,,若,则___________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据向量垂直，数量积为0列方程求解即可.‎ ‎【详解】由题：，所以，‎ 所以，‎ 解得：.‎ 故答案为：‎ ‎【点睛】此题考查向量数量积的坐标运算，根据两个向量垂直，数量积为0建立方程计算求解.‎ ‎10.在公差不为零的等差数列{an}中,a1=2,且a1,a3,a7依次成等比数列,那么数列{an}的前n项和等于____________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据a1,a3,a7依次成等比数列,求出公差，即可求解.‎ ‎【详解】在公差不为零的等差数列{an}中,a1=2,设公差为 且a1,a3,a7依次成等比数列,即，‎ ‎，，所以，‎ 所以数列{an}的前n项和.‎ 故答案为：‎ ‎【点睛】此题考查等差数列基本量的计算，根据等比中项的关系列出方程解出公差，根据公式进行数列求和.‎ ‎11.已知中心在原点的双曲线的右焦点坐标为,且两条渐近线互相垂直,则此双曲线的标准方程为_____.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据两条渐近线互相垂直得出渐近线方程，即求出的值，结合焦点坐标即可求解.‎ ‎【详解】由题双曲线焦点在轴，设双曲线方程，‎ 两条渐近线互相垂直，即，得，‎ 又因为右焦点坐标为,‎ 所以，‎ 解得，‎ 所以双曲线的标准方程为：.‎ 故答案为：‎ ‎【点睛】此题考查根据渐近线的关系结合焦点坐标求双曲线的基本量，进而得出双曲线的标准方程，考查通式通法和基本计算.‎ ‎12.在中, ,,,则____.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据正弦定理建立等量关系求解即可.‎ ‎【详解】在中,由正弦定理得：，‎ 所以 ‎.‎ 故答案为：‎ ‎【点睛】此题考查正弦定理的应用，结合三角恒等变换二倍角公式，求三角函数值，关键在于准确掌握基本计算方法正确求解.‎ ‎13.已知均为大于0的实数,给出下列五个论断:①,②,③,④,⑤.以其中的两个论断为条件,余下的论断中选择一个为结论,请你写出一个正确的命题___________.‎ ‎【答案】①③推出⑤(答案不唯一还可以①⑤推出③等)‎ ‎【解析】‎ ‎【分析】‎ 选择两个条件根据不等式性质推出第三个条件即可，答案不唯一.‎ ‎【详解】已知均为大于0的实数,选择①③推出⑤.‎ ‎①，③，‎ 则，‎ 所以.‎ 故答案为：①③推出⑤‎ ‎【点睛】此题考查根据不等式的性质比较大小，在已知条件中选择两个条件推出第三个条件，属于开放性试题，对思维能力要求比较高.‎ ‎14.如图,某城市中心花园的边界是圆心为O,直径为‎1千米的圆,花园一侧有一条直线型公路l,花园中间有一条公路AB(AB是圆O的直径),规划在公路l上选两个点P,Q,并修建两段直线型道路PB,QA.规划要求:道路PB,QA不穿过花园.已知,(C､D为垂足),测得OC=0.9,BD=1.2(单位:千米).已知修建道路费用为m元/千米.在规划要求下,修建道路总费用的最小值为_____元.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据几何关系考虑道路不穿过花园，求解最小距离，即可得到最小费用.‎ ‎【详解】‎ 如图：过点作直线交于，取与圆的交点，‎ 连接，则，‎ 过点作直线交于，‎ 过点作直线交于，‎ 根据图象关系可得，直线上，点左侧的点与连成线段不经过圆内部，‎ 点右侧的点与连成的线段不经过圆的内部，‎ 最短距离之和即，‎ 根据几何关系：，，‎ 所以，‎ 所以，‎ ‎，所以，‎ 最小距离为2.1千米.‎ 修建道路总费用的最小值为元.‎ 故答案为：‎ ‎【点睛】此题考查与圆相关的几何性质，根据几何性质解决实际问题，需要注意合理地将实际问题抽象成纯几何问题求解.‎ 三､解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.‎ ‎15.已知函数.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)求f(x)在区间上的最大值和最小值.‎ ‎【答案】(1)；(2) 最小值0；最大值 ‎【解析】‎ ‎【分析】‎ ‎（1）对函数进行三角恒等变换得，即可得最小正周期；‎ ‎（2）整体考虑的取值范围，求出最大值和最小值.‎ ‎【详解】解: ‎ ‎(1) f(x)最小正周期T =；‎ ‎(2)因为,所以 所以当,即时,f(x)取得最小值；‎ 当,即时,f(x)取得最大值，‎ 所以f(x)在区间上的最小值0；最大值.‎ ‎【点睛】此题考查利用三角恒等变换对函数进行化简，求最小正周期和闭区间上的值域，关键在于利用公式准确化简，正确求值.‎ ‎16.为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:‎ ‎ 比例 学校 等级 学校A 学校B 学校C 学校D 学校E 学校F 学校G 学校H 优秀 ‎8%‎ ‎3%‎ ‎2%‎ ‎9%‎ ‎1%‎ ‎22%‎ ‎2%‎ ‎3%‎ 良好 ‎37%‎ ‎50%‎ ‎23%‎ ‎30%‎ ‎45%‎ ‎46%‎ ‎37%‎ ‎35%‎ 及格 ‎22%‎ ‎30%‎ ‎33%‎ ‎26%‎ ‎22%‎ ‎17%‎ ‎23%‎ ‎38%‎ 不及格 ‎33%‎ ‎17%‎ ‎42%‎ ‎35%‎ ‎32%‎ ‎15%‎ ‎38%‎ ‎24%‎ ‎(1)从8所学校中随机选出一所学校,求该校为先进校的概率；‎ ‎(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列；‎ ‎(3)设8所学校优秀比例的方差为S12,良好及其以下比例之和的方差为S22,比较S12与S22的大小.(只写出结果)‎ ‎【答案】(1) ；(2)见解析； (3)S12=S22‎ ‎【解析】‎ ‎【分析】‎ ‎（1）统计出健康测试成绩达到良好及其以上的学校个数，即可得到先进校的概率；‎ ‎（2）根据表格可得：学生不及格率低于30%的学校有学校B､F､H三所, 所以X的取值为0,1,2，分别计算出概率即可得到分布列；‎ ‎（3）考虑优秀的比例为随机变量Y，则良好及以下的比例之和为Z=1-Y，根据方差关系可得两个方差相等.‎ ‎【详解】解:( 1)8所学校中有ABEF四所学校学生的体质健康测试成绩达到良好及其以上的比例超过40% , ‎ 所以从8所学校中随机取出一所学校,该校为先进校的概率为；‎ ‎(2)8所学校中,学生不及格率低于30%的学校有学校B､F､H三所,所以X的取值为0,1,2. ‎ ‎ ‎ 所以随机变量X的分布列为：‎ X ‎0‎ ‎1‎ ‎2‎ P ‎(3)设优秀的比例为随机变量Y，则良好及以下的比例之和为Z=1-Y，‎ 则，‎ 所以：S12=S22.‎ ‎【点睛】此题考查简单几何概率模型求概率，求分布列，以及方差关系的辨析，关键在于熟练掌握分布列的求法和方差关系.‎ ‎17.如图,在四棱锥S-ABCD中,底面ABCD为直角梯形,AD//BC,∠SAD =∠DAB= ,SA=3,SB=5,,,. ‎ ‎(1)求证:AB平面SAD；‎ ‎(2)求平面SCD与平面SAB所成的锐二面角的余弦值；‎ ‎(3)点E,F分别为线段BC,SB上的一点,若平面AEF//平面SCD,求三棱锥B-AEF的体积.‎ ‎【答案】(1) 见解析；(2) ； (3)1‎ ‎【解析】‎ 分析】‎ ‎（1）通过证明，得线面垂直；‎ ‎（2）结合第一问结论，建立空间直角坐标系，求出两个平面的法向量，即可得二面角的余弦值；‎ ‎（3）根据面面平行关系得出点F的位置，即可得到体积.‎ ‎【详解】(1)证明:在中,因为,‎ 所以. ‎ 又因为∠DAB=900‎ 所以, ‎ 因为 所以平面SAD. ‎ ‎(2)解:因为 AD,,， ‎ 建立如图直角坐标系：‎ 则A(0,0,0)B(0,4,0), C(2,4,0),D(1,0,0),S(0,0,3).‎ 平面SAB的法向量为.‎ 设平面SDC的法向量为 所以有 即,‎ 令，‎ 所以平面SDC的法向量为 ‎ 所以 ‎ ‎(3)因为平面AEF//平面SCD,‎ 平面AEF平面ABCD=AE,平面SCD平面ABCD=CD,‎ 所以,‎ 平面AEF平面SBC=EF,平面SCD平面SBC=SC,‎ 所以 由,AD//BC 得四边形AEDC为平行四边形.‎ 所以E为BC中点. ‎ 又,‎ 所以F为SB中点.‎ 所以F到平面ABE的距离为,‎ 又的面积为2,‎ 所以.‎ ‎【点睛】此题考查立体几何中的线面垂直的证明和求二面角的大小，根据面面平行的性质确定点的位置求锥体体积.‎ ‎18.已知椭圆C:的长轴长为4,离心率为,点P在椭圆C上.‎ ‎(1)求椭圆C的标准方程；‎ ‎(2)已知点M (4,0),点N(0,n),若以PM为直径的圆恰好经过线段PN的中点,求n的取值范围.‎ ‎【答案】(1) ； (2) .‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据长轴长和离心率求出标准方程；‎ ‎（2）取PN的中点为Q，以PM为直径的圆恰好经过线段PN的中点，所以MQ⊥NP,根据垂直关系建立等量关系，结合点P的坐标取值范围，即可得解.‎ ‎【详解】解:( 1)由椭圆的长轴长‎2a=4,得a=2‎ 又离心率,所以 所以.‎ 所以椭圆C的方程为：. ‎ ‎(2)法一:设点,则 所以PN的中点 ‎,，‎ 因为以PM为直径的圆恰好经过线段PN的中点 所以MQ⊥NP,则， ‎ 即，‎ 又因为,所以，‎ 所以，‎ 函数的值域为 所以 所以. ‎ 法二:设点,则.‎ 设PN的中点为Q 因为以PM为直径的圆恰好经过线段PN的中点 所以MQ是线段PN的垂直平分线，‎ 所以 即 所以，‎ 函数的值域为 所以，‎ 所以.‎ ‎【点睛】此题考查求椭圆的标准方程，根据垂直关系建立等量关系，结合椭圆上的点的坐标特征求出取值范围.‎ ‎19.已知函数.‎ ‎(1)求曲线在点处的切线方程；‎ ‎(2)求函数零点的个数.‎ ‎【答案】(1) ；(2)零点的个数为2.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）求出导函数，得出，即可得到切线方程；‎ ‎（2）根据为偶函数，只需讨论在的零点个数，结合导函数分析单调性即可讨论.‎ ‎【详解】解:( 1)因为,‎ 所以， ‎ 又因为，‎ 所以曲线在点处的切线方程为；‎ ‎(2)因为为偶函数, ‎ 所以要求在上零点个数,‎ 只需求在上零点个数即可. ‎ 令,得,， ‎ 所以在单调递增,在单调递减,在单调递增,‎ 在单调递减,在单调递增 列表得:‎ ‎…‎ ‎0‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎…‎ ‎1‎ ‎↗‎ 极大值 ‎↘‎ 极小值 ‎↗‎ 极大值 ‎↘‎ 极小值 ‎…‎ 由上表可以看出在()处取得极大值,在()处取得极小值，‎ ‎; ‎ ‎. ‎ 当且时 ‎ ‎(或,) ‎ 所以在上只有一个零点 函数零点的个数为2.‎ ‎【点睛】此题考查求函数在某点处的切线方程，求函数零点的个数，根据奇偶性分类讨论，结合单调性和极值分别考虑函数值的符号得解.‎ ‎20.已知项数为的数列满足如下条件:①；②.若数列满足,其中,则称为的“伴随数列”.‎ ‎(1)数列1,3,5,7,9是否存在“伴随数列”,若存在,写出其“伴随数列”；若不存在,请说明理由；‎ ‎(2)若为的“伴随数列”,证明:；‎ ‎(3)已知数列存在“伴随数列”,且,,求m的最大值.‎ ‎【答案】(1) 不存在“伴随数列”，见解析 ；(2) 见解析；(3)33‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据“伴随数列”的定义检验即可判定；‎ ‎（2）根据“伴随数列”的定义，结合数列的单调性讨论的符号即可得解；‎ ‎（3）根据数列和其“伴随数列”项的特征，结合单调性分析出，即可求解.‎ ‎【详解】(1)解:数列1,3,5,7,9不存在“伴随数列” ‎ 因为, ‎ ‎ 所以数列1,3,5,7,9不存在“伴随数列”. ‎ ‎(2)证明:因为, ‎ 又因为,所以有 ‎ 所以 ‎ 所以 成立 ‎ ‎(3)1≤ij ≤m,都有, ‎ 因为,.‎ 所以,‎ 所以 ‎ 所以 因为,‎ 所以 ‎ 又 ‎=‎ 所以,‎ 所以 ‎ 又,‎ 所以 ‎ 例如:(),满足题意,‎ 所以m的最大值是33.‎ ‎【点睛】此题考查数列新定义相关问题，关键在于读懂题意，建立恰当的等量关系或不等关系，求解得值，综合性比较强.‎