湖北省各地2017届高三最新考试数学文试题分类汇编：统计与概率+Word版

湖北省各地2017届高三最新考试数学文试题分类汇编：统计与概率+Word版

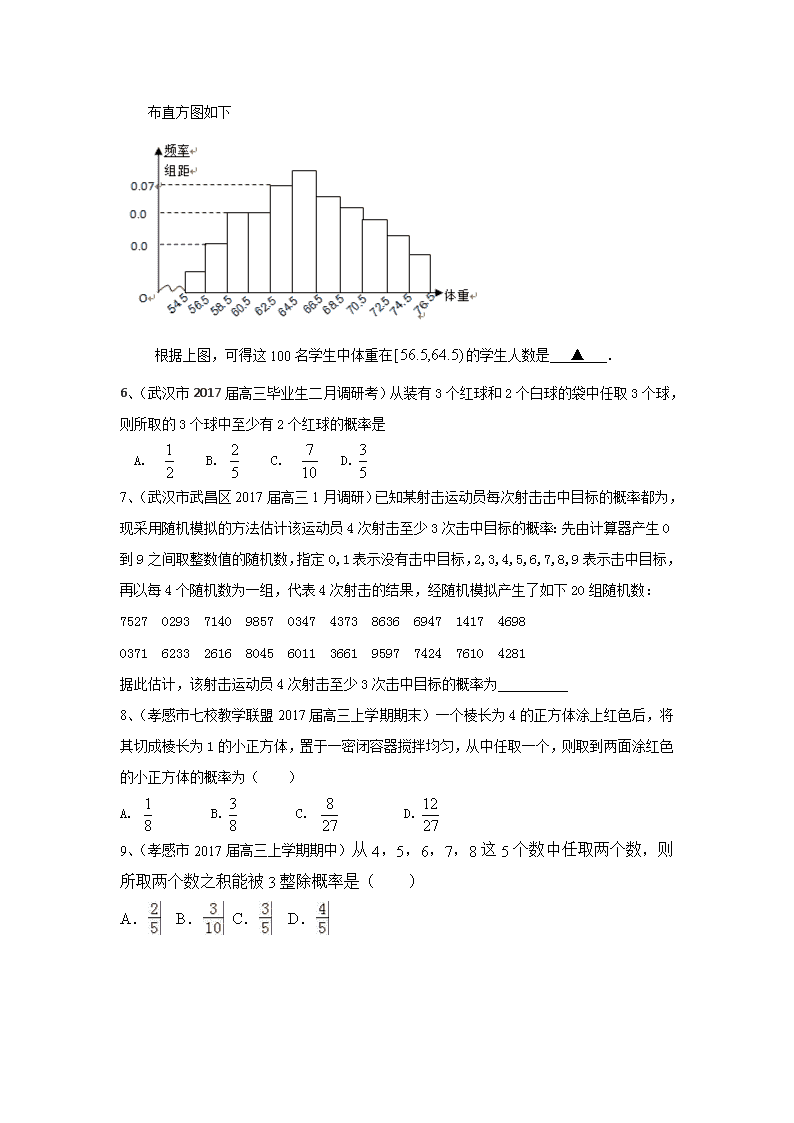
湖北省各地2017届高三最新考试数学文试题分类汇编 统计与概率　2017.02‎ 一、选择、填空题 ‎1、（荆、荆、襄、宜四地七校考试联盟2017届高三2月联考）从数字中任取两个不同的数字构成一个两位数，这个两位数大于的概率是 A． B． C． D．‎ ‎2、（荆州市五县市区2017届高三上学期期末）经统计，用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系．‎ 对某小组学生每周用于数学的学习时间与数学成绩进行数据收集如下：‎ 由表中样本数据求得回归方程为，‎ 则点与直线的位置关系是（ ）‎ A．点在直线左侧 B．点在直线右侧 C．点在直线上 D．无法确定 ‎3、（天门、仙桃、潜江市2017届高三上学期期末联合考试）对于一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为P1，P2，P3，则 ‎ ‎ A．P1= P2＜P3 B．P2= P3＜P1 C．P1= P2=P3 D．P1= P3＜P2‎ ‎4、（天门、仙桃、潜江市2017届高三上学期期末联合考试）已知集合，，在集合中任取一个元素,则“”的概率为 A． B． C． D．‎ ‎5、（天门、仙桃、潜江市2017届高三上学期期末联合考试）‎ 为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁~18岁的男生体重（kg），得到频率分布直方图如下 ‎ ‎ ‎ 根据上图，可得这100名学生中体重在的学生人数是 ▲ ．‎ ‎6、（武汉市2017届高三毕业生二月调研考）从装有3个红球和2个白球的袋中任取3个球，则所取的3个球中至少有2个红球的概率是 ‎ A. B. C. D.‎ ‎7、（武汉市武昌区2017届高三1月调研）已知某射击运动员每次射击击中目标的概率都为，现采用随机模拟的方法估计该运动员4次射击至少3次击中目标的概率：先由计算器产生0到9之间取整数值的随机数，指定0,1表示没有击中目标，2,3,4,5,6,7,8,9表示击中目标，再以每4个随机数为一组，代表4次射击的结果，经随机模拟产生了如下20组随机数：‎ ‎7527 0293 7140 9857 0347 4373 8636 6947 1417 4698‎ ‎0371 6233 2616 8045 6011 3661 9597 7424 7610 4281‎ 据此估计，该射击运动员4次射击至少3次击中目标的概率为 ‎ ‎8、（孝感市七校教学联盟2017届高三上学期期末）一个棱长为4的正方体涂上红色后，将其切成棱长为1的小正方体，置于一密闭容器搅拌均匀，从中任取一个，则取到两面涂红色的小正方体的概率为（ ）‎ A. B. C. D.‎ ‎9、（孝感市2017届高三上学期期中）从4，5，6，7，8这5个数中任取两个数，则所取两个数之积能被3整除概率是（　　）‎ A． B． C． D．‎ 二、解答题 ‎1、（黄冈市2017届高三上学期期末）某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下：‎ 甲运动员得分：13,51,23,8,26,38,16,33,14,28,39；‎ 乙运动员得分：49,24,12，31,50,31,44,36,15,37,25,36,39.‎ ‎ （1）用十位数为茎，在答题卡中画出原始数据的茎叶图；‎ ‎ （2）用分层抽样的方法在乙运动员得分十位数为2,3,4的比赛中抽取一个容量为5的样本，从该样本中随机抽取2场，求其中恰有1场得分大于40分的概率.‎ ‎2、（荆、荆、襄、宜四地七校考试联盟2017届高三2月联考）某手机厂商推出一款吋大屏手机，现对名该手机使用者（名女性，名男性）进行调查，对手机进行打分，打分的频数分布表如下：‎ 女性用户：‎ 分值区间 频数 男性用户：‎ 分值区间 频数 ‎（Ⅰ）完成下列频率分布直方图，并比较女性用户和男性用户评分的波动大小（不要求计算具体值，给出结论即可）；‎ ‎（Ⅱ）分别求女性用户评分的众数，男性用户评分的中位数；‎ ‎（Ⅲ）如果评分不低于分，就表示该用户对手机“认可”，否则就表示“不认可”，完成下列列联表，并回答是否有的把握认为性别和对手机的“认可”有关；‎ 女性用户 男性用户 合计 ‎“认可”手机 ‎“不认可”手机 合计 附：‎ ‎3、（荆门市2017届高三元月调考） 某中学对高三学生进行体能测试，已知高三某文科班有学生30人，立定跳远的测试成绩用茎叶图表示如下图（单位：cm）；男生成绩在195cm以上（包括195cm）定义为“合格”， 成绩在195cm以下（不包括195cm）定义为“不合格”； 女生成绩在185cm以上（包括185cm）定义为“合格”， 成绩在185cm以下（不包括185cm）定义为“不合格”.‎ ‎ （Ⅰ）求女生立定跳远测试成绩的中位数；‎ ‎（Ⅱ）若在男生中按成绩是否合格进行分层抽样，抽取6人，求抽取成绩为“合格”的学生人数；‎ ‎（Ⅲ）若从（Ⅱ）的抽取6名男生中任意选取4人，求这4人中至少有3人“合格”的概率.‎ ‎4、（荆州市五县市区2017届高三上学期期末）某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：[50，100），[100，150），[150，200），[200，250），[250，300]，绘制成如图所示的频率分布直方图．‎ ‎（Ⅰ）求直方图中x的值；‎ ‎（Ⅱ）求续驶里程在[200，300]的车辆数；‎ ‎（Ⅲ）从续驶里程在[200，300]的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为[200，250）的概率．‎ ‎5、（武汉市2017届高三毕业生二月调研考）如图所示茎叶图记录了甲、乙两组5名工人制造某种零件的个数 ‎（1）求甲组工人制造零件的平均数和方差；‎ ‎ （2）分别从甲、乙两组中随机选取一个工人，求这两个工人制造的零件总数不超过20的概率.‎ ‎6、（武汉市武昌区2017届高三1月调研）我国上是世界严重缺水的国家，城市缺水问题较为突出，某市政府为了鼓励居民节约用水，计划在本市试行居民生活用水定额管理，即确定一个合理的居民月用水量标准（吨），用水量不超过的部分按平价收费，超过的部分按议价收费，为了了解全市民月用水量的分布情况，通过抽样，获得了100位居民某年的月用水量（单位：吨），将数据按照，，…，分成9组，制成了如图所示的频率分布直方图.‎ ‎（Ⅰ）求直方图中 的值；‎ ‎（Ⅱ）已知该市有80万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；‎ ‎（Ⅲ）若该市政府希望使的居民每月的用水量不超过标准（吨），估计的值，并说明理由；‎ ‎7、（襄阳市优质高中2017届高三1月联考） 某研究小组到社区了解参加健美操运动人员的情况，用分层抽样的方法抽取了40人进行调查，按照年龄分成五个小组：，并绘制成如图所示的频率分布直方图.‎ ‎（1）求该社区参加健美操运动人员的平均年龄；‎ ‎ （2）如果研究小组从该样本中年龄在和的6人中随机地抽取出2人进行深入采访，求被采访的2人，年龄恰好都在内的概率.‎ ‎8、（孝感市七校教学联盟2017届高三上学期期末）‎ 孝汉城铁于12月1日开通，C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了乘车次数的频率分布直方图和频数分布表。‎ 乘车次数分组 频数 ‎[0,5)‎ ‎15‎ ‎[5,10)‎ ‎20‎ ‎[10,15)‎ ‎25‎ ‎[15,20)‎ ‎24‎ ‎[20,25)‎ ‎11‎ ‎[25,30]‎ ‎5‎ ‎ C5302次乘客月乘坐次数频率分布直方图 C5321次乘客月乘坐次数频数分布表 ‎（1）若将频率视为概率，月乘车次数不低于15次的称之为“老乘客”，试问：哪一车次的“老乘客”较多，简要说明理由。‎ ‎（2）已知在C5321次列车随机抽到的50岁以上人员有35名，其中有10名是“老乘客”，由条件完成下面列联表，并根据资料判断，是否有90 %的把握认为年龄有乘车次数有关，说明理由。‎ 老乘客 新乘客 合计 ‎50岁以上 ‎50岁以下 合计 附：随机变量 （其中n=a+b+c+d为样本总量）‎ P()‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎9、（荆州中学2017届高三1月质量检测）某学校的篮球兴趣小组为调查该校男女学生对篮球的喜好情况，用简单随机抽样方法调查了该校名学生，调查结果如下：‎ ‎（1）该校共有名学生，估计有多少学生喜好篮球？‎ ‎（2）能否有%的把握认为该校的学生是否喜欢篮球与性别有关？说明原因；‎ ‎（3）已知在喜欢篮球的名女生中，名女生（分别记为同时喜欢乒乓球，‎ 名女生(分别记为）同时喜欢羽毛球，名女生(分别记为同时喜欢排球，现从喜欢乒乓球、羽毛球、排球的女生中各取人，求不全被选中的概率．‎ 附：，．‎ 参考数据：‎ 参考答案 一、选择、填空题 ‎1、B　　2、C　　3、C　　4、A　　5、40　　　6、C ‎7、0.75　　8、B　　9、A 二、解答题 ‎1、解：（Ⅰ）由题意得茎叶图如图：…………………………………………（5分）‎ ‎（Ⅱ）用分层抽样的方法在乙运动员得分十位数为2、3、4‎ 的比赛中抽取一个容量为5的样本，‎ 则得分十位数为2、3、别应该抽取1，3，1场，‎ 所抽取的赛场记为A，B1，B2，B3，C，‎ 从中随机抽取2场的基本事件有：‎ ‎（A，B1），（A，B2），（A，B3），（A，C），‎ ‎（B1，B2），（B1，B3），（B1，C），（B2，B3），‎ ‎（B2，C），（B3，C）共10个，‎ 记“其中恰有1场的得分大于4”为事件A，‎ 则事件A中包含的基本事件有：‎ ‎（A，C），（B1，C），（B2，C），（B3，C）共4个，‎ ‎∴…………………………………………………………（12分）‎ 答：其中恰有1场的得分大于4的概率为．‎ ‎2、（Ⅰ）女性用户和男性用户的频率分布表分别如下左、右图：‎ 由图可得女性用户的波动小，男性用户的波动大． ……………………………………4分 ‎（Ⅱ）由女性用户频率分布直方图知，女性用户评分的众数为； …………………5分 在男性用户频率分布直方图中，中位数两边的面积相等。设中位数为，则 于是，解得 ……………………8分 ‎（Ⅲ）列联表如下图：‎ 女性用户 男性用户 合计 ‎“认可”手机 ‎140‎ ‎180‎ ‎320‎ ‎“不认可”手机 ‎60‎ ‎120‎ ‎180‎ 合计 ‎200‎ ‎300‎ ‎500‎ ‎，所以有的把握认为性别和对手机的“认可”有关． ……………………………………12分 ‎3、（Ⅰ）女生立定跳远成绩的中位数为（） ……………………………3分 ‎（Ⅱ）男生成绩“合格”的有8人，“不合格”的有4人，用分层抽样的方法，其中成绩 “合格”的学生应抽取（人） ……………………………………………………7分 ‎(III)由（Ⅱ）可知6人中，4人合格，2人不合格 设合格学生为 a,b,c,d ，不合格学生为e,f ，从这6人中任取4人有 abcd abce abcf abde abdf abef acde acdf acef adef ‎ bcde bcdf bcef bdef cdef …………………10分 共有15个基本事件，其中符合条件的基本事件共有9个，故. …………12分 ‎4、（Ⅰ）由直方图可得：（0.002+0.005+0.008+x+0.002）×50=1，∴x=0.003；（4分）‎ ‎（Ⅱ）由题意可知，续驶里程在[200，300]的车辆数为：20×（0.003×50+0.002×50）=5；（8分）‎ ‎（Ⅲ）由（Ⅱ）及题意可知，续驶里程在[200，250）的车辆数为3，‎ 续驶里程在[250，300]的车辆数为2，‎ 从这5辆中随机抽取2辆车，共有10种抽法；(列举略)‎ 其中恰有一辆汽车的续驶里程为[200，250）抽法有6种，‎ ‎∴恰有一辆车的续驶里程为[200，250）的概率为0.6 . （12分）‎ ‎5、‎ ‎6、（Ⅰ）由频率分布直方图，可得 ‎，‎ 解得.‎ ‎（Ⅱ）由频率分布直方图可知，100位居民每人月用水量不低于3吨的人数为 ‎ ，‎ 由以上样本频率分布，可以估计全市80万居民中月均用水量不低于3吨的人数为 ‎ .‎ ‎(Ⅲ) 前6组的频率之和为 ，‎ 而前5组的频率之和为 ，‎ ‎ ‎ 由 ，解得，‎ 因此，估计月用水量标准为2.9吨时，85%的居民每月的用水量不超过标准.‎ ‎7、解：（I），该社区参加健美操运动人员的平均年龄为57.5岁；……………………5分 ‎（II）年龄在的人员2人，依次记为、，年龄在的人员4人，依次记为、、、，从这6人中随机地选出2人有15种等可能的结果：、、、 、、、、、、、、、、、；‎ 记事件：被采访的2人年龄恰好都在，则包含6种结果，.所以，被采访的2人年龄恰好都在的概率为．……………………12分 ‎8、（1）C5302次“老乘客”的概率为，‎ C5321次“老乘客”的概率为：‎ ‎，5302次老乘客较多。 （6分）‎ ‎（2）‎ 老乘客 新乘客 合计 ‎50岁以上 ‎10‎ ‎25‎ ‎35‎ ‎50岁以下 ‎30‎ ‎35‎ ‎65‎ ‎ 合计 ‎40‎ ‎60‎ ‎100‎ ‎ （10分）‎ ‎90 %的把握认为年龄与乘车次数有关。 （12分）‎ ‎9、‎