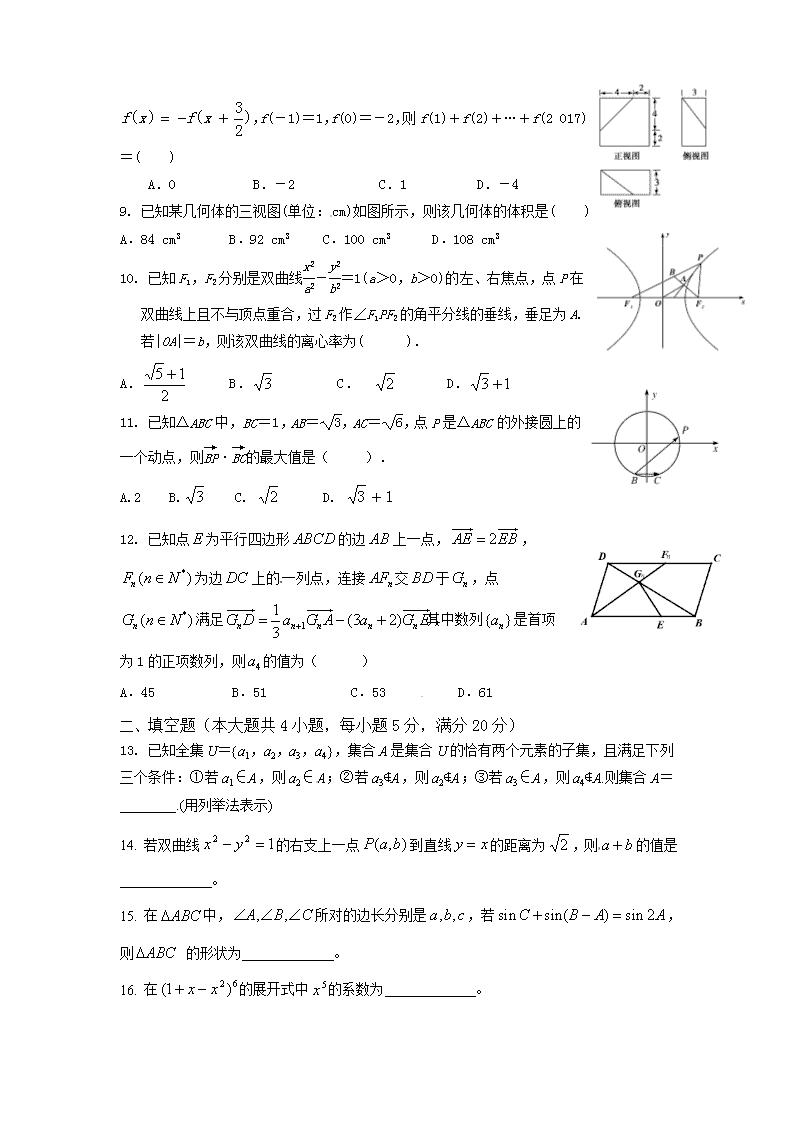
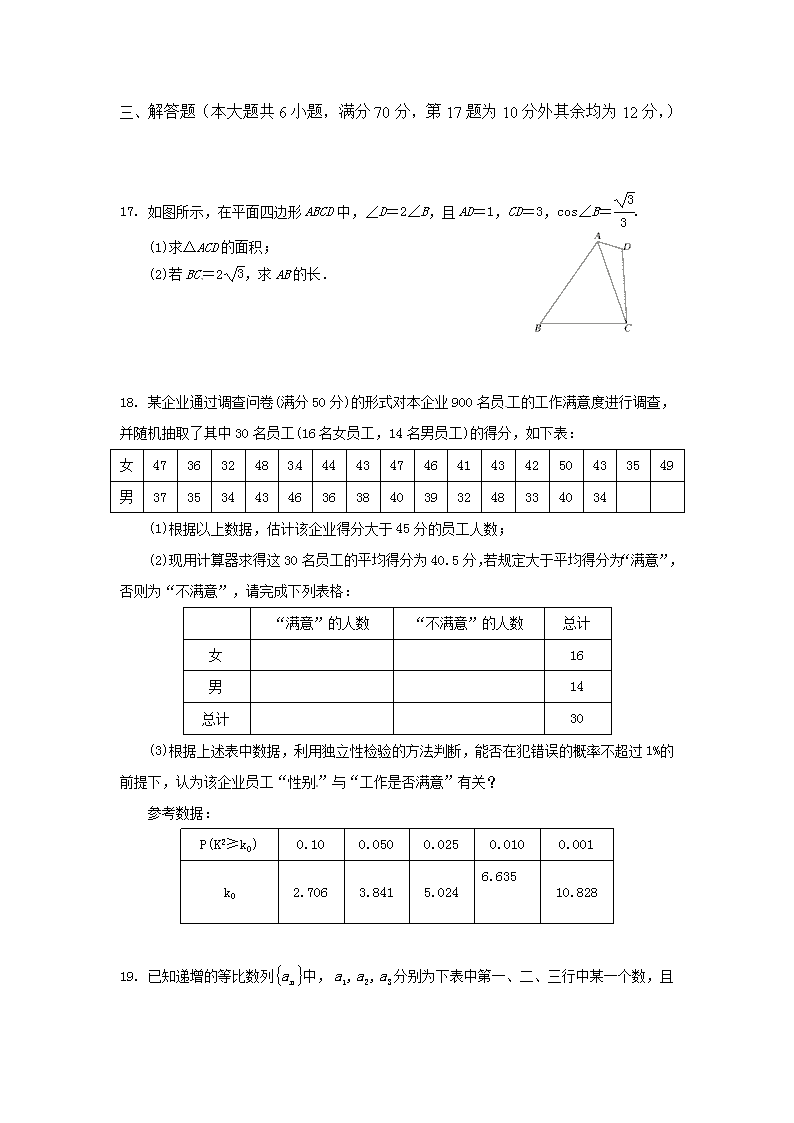
数学理卷·2017届重庆十一中高三12月月考(2016
重庆市第十一中学高2017级12月月考
数 学 试 题(理科)
命题人:甄振国 审题人:马凯
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1. 已知全集U=R,集合A={x|0
6.635,查表得P(K2≥6.635)=0.010.
∴能在犯错误的概率不超过1%的前提下,认为性别与工作是否满意有关.
19. 解:(I)当时,不合题意;
当时,当且仅当时,符合题意;
当时,不合题意。因此
所以公式q=3,故【来源:全,品…中&高*考+网】 (II)因为
所 所以当n为偶数时,综上所述,
所以当n为偶数时,
20. 解:(1)由已知,又,,
则有,则,又,则有面
(2)由(I)面,则,又,,取的中点,则直线两两垂直,建立如图所示的直角坐标系,
则有,,,,则,,,则求得的法向量,
的法向量,又,
则与垂直。
即二面角的大小为
21.解:(1)抛物线C1的焦点F(0,1),
椭圆C2的左焦点F1(-,0),则|FF1|=.【来源:全,品…中&高*考+网】
(2)设直线AB:y=kx+m,A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由得x2-4kx-4m=0,
故x1+x2=4k,x1x2=-4m.由x2=4y,得y′=,
故切线PA,PB的斜率分别为kPA=,kPB=,
再由PA⊥PB,得kPAkPB=-1,即·===-m=-1,
故m=1,这说明直线AB过抛物线C1的焦点F.
由得x==2k,
y=·2k-=kx1-=·x1-==-1,即P(2k,-1).
于是点P(2k,-1)到直线AB:kx-y+1=0的距离d==2.
由得(1+2k2)x2+4kx-2=0,
从而|CD|= = ,
同理,|AB|=4(1+k2)
若|AB|,d,|CD|成等比数列,则d2=|AB|·|CD|,
即(2)2=4(1+k2)· ,
化简整理,得28k4+36k2+7=0,此方程无实根,
所以不存在直线AB,使得|AB|,d,|CD|成等比数列
22. 解:⑴. 令,
要使在定义域内是增函数,只需在内恒成立.
由题意,的图象为开口向上的抛物线,
对称轴方程为,
∴,只需,即时,
∴在内为增函数,正实数的取值范围是.
⑵∵在上是减函数,∴时,;时,,
即,
① 当时,,其图象为开口向下的抛物线,对称轴在轴
的左侧,且,所以在内是减函数.当时,,因为,所以,,此时,在内是减函数.故∴当时,在上单调递减,不合题意;
② 当时,由,所以.
又由⑵知当时,在上是增函数,
∴,不合题意;
③ 当时,由⑵知在上是增函数,,
又在上是减函数,
故只需,,而,,
即,解得 综上所述,实数的取值范围是.