2019四川省攀枝花中考数学试卷（解析版)

2019四川省攀枝花中考数学试卷（解析版)

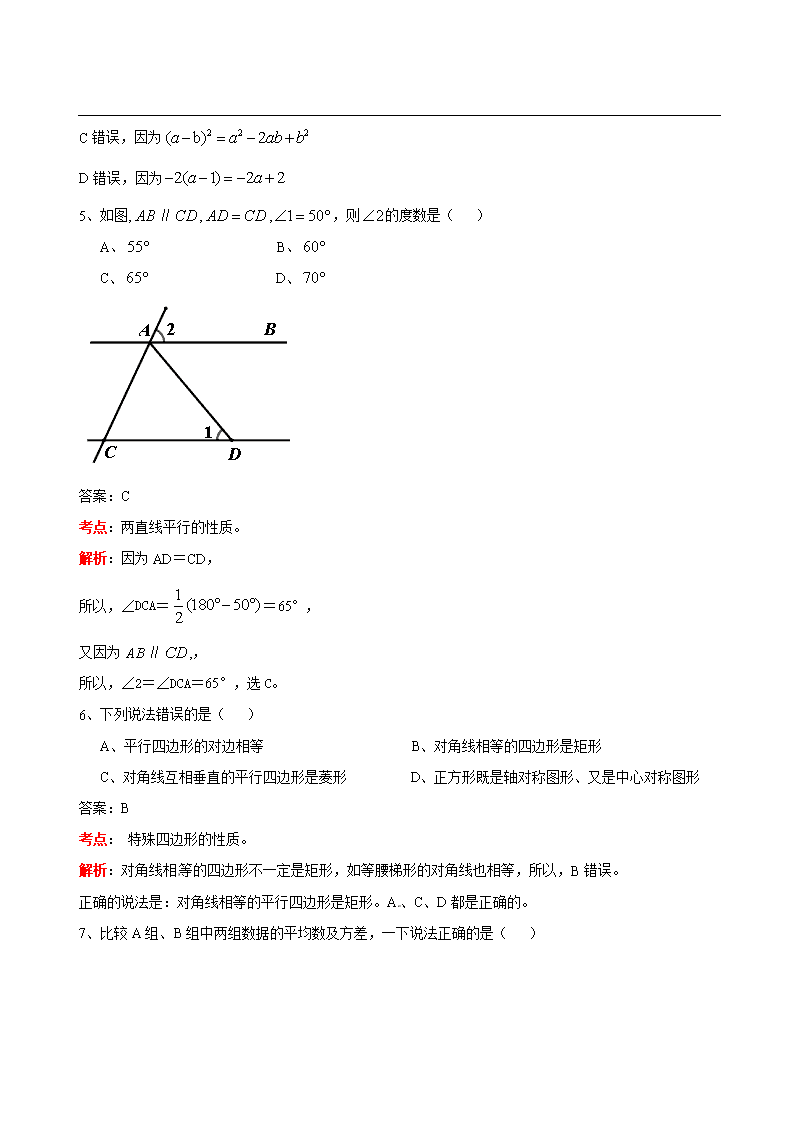
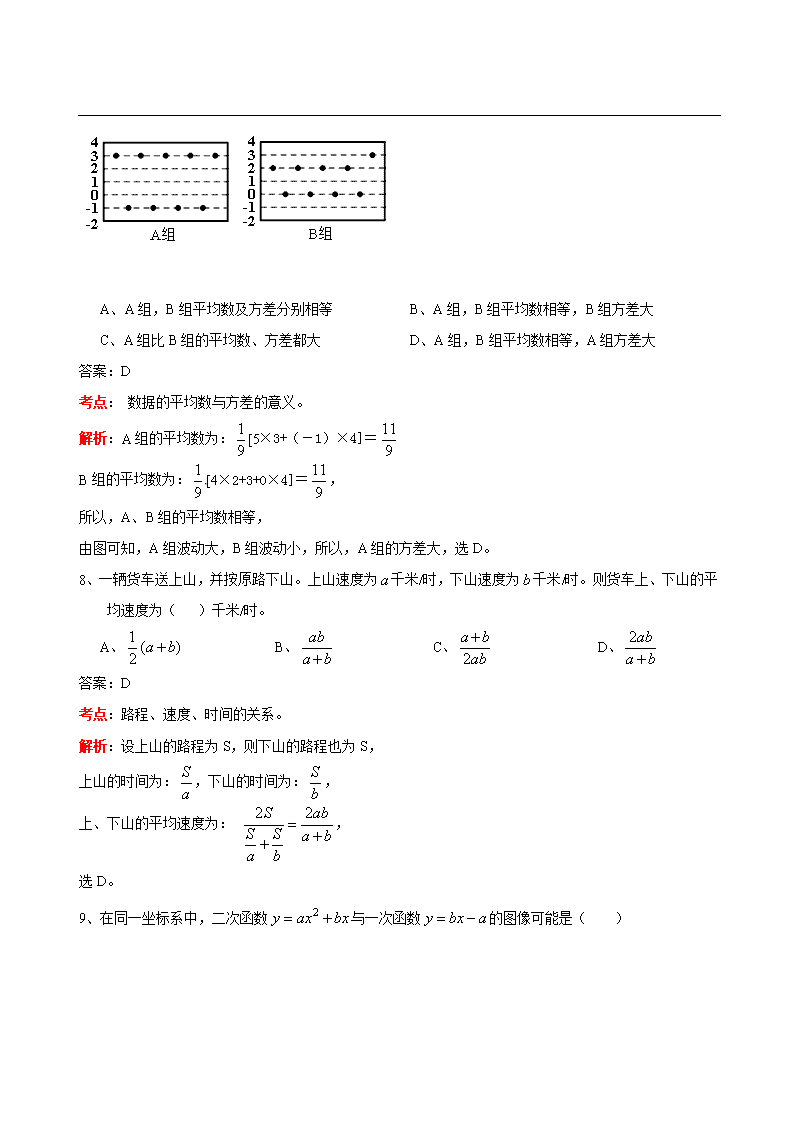
攀枝花市2019年中考数学试题 一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中只有一项是符合题目要求的。‎ ‎1、等于（ ）[来源:Zxxk.Com]‎ ‎ A、 B、 C、 D、‎ 答案：B 考点：乘方运算。‎ 解析：（－1）2＝（－1）×（－1）＝1‎ ‎2、在，，，这四个数中，绝对值最小的数是（ ）‎ ‎ A、 B、 C、 D、‎ 答案：A 考点： 实数的绝对值。‎ 解析：｜0｜＝0，｜－1｜＝1，｜2｜＝2，｜－3｜＝3‎ 显然0最小，所以，选A。‎ ‎3、用四舍五入法将精确到千位，正确的是（ ）‎ ‎ A、 B、 C、 D、‎ 答案：C （A答案是精确到个位，所以错误）‎ 考点：科学记数法。‎ 解析：把一个数表示成a与10的n次幂相乘的形式（1≤a<10，n为整数），这种记数法叫做科学记数法。‎ 所以，130542＝1.30542×105，‎ 又精确到千位，所以，130542＝1.30542×105≈1.31×105‎ ‎4、下列运算正确的是（ ）‎ ‎ A、 B、 ‎ ‎ C、 D、‎ 答案：A 考点：整式的运算。‎ 解析：合并同类项，可知，A正确；‎ B、错误，因为 C错误，因为 D错误，因为 ‎5、如图,∥,,，则的度数是（ ）‎ ‎ A、 B、 ‎ ‎ C、 D、‎ 答案：C 考点：两直线平行的性质。‎ 解析：因为AD＝CD，[来源:学.科.网]‎ 所以，∠DCA＝＝65°，‎ 又因为∥,，‎ 所以，∠2＝∠DCA＝65°，选C。‎ ‎6、下列说法错误的是（ ）‎ ‎ A、平行四边形的对边相等 B、对角线相等的四边形是矩形 ‎ C、对角线互相垂直的平行四边形是菱形 D、正方形既是轴对称图形、又是中心对称图形 答案：B 考点： 特殊四边形的性质。‎ 解析：对角线相等的四边形不一定是矩形，如等腰梯形的对角线也相等，所以，B错误。‎ 正确的说法是：对角线相等的平行四边形是矩形。A、C、D都是正确的。‎ ‎7、比较A组、B组中两组数据的平均数及方差，一下说法正确的是（ ）‎ ‎ A、A组，B组平均数及方差分别相等 B、A组，B组平均数相等，B组方差大 ‎ C、A组比B组的平均数、方差都大 D、A组，B组平均数相等，A组方差大 答案：D 考点： 数据的平均数与方差的意义。‎ 解析：A组的平均数为：[5×3+（－1）×4]＝‎ B组的平均数为：[4×2+3+0×4]＝，‎ 所以，A、B组的平均数相等，‎ 由图可知，A组波动大，B组波动小，所以，A组的方差大，选D。‎ ‎8、一辆货车送上山，并按原路下山。上山速度为千米/时，下山速度为千米/时。则货车上、下山的平均速度为（ ）千米/时。‎ ‎ A、 B、 C、 D、‎ 答案：D 考点：路程、速度、时间的关系。‎ 解析：设上山的路程为S，则下山的路程也为S，‎ 上山的时间为：，下山的时间为：，‎ 上、下山的平均速度为： ，‎ 选D。‎ ‎9、在同一坐标系中，二次函数与一次函数的图像可能是（ ）‎ 答案：C ‎ 考点：二次函数与一次函数的图象。‎ 解析：一次函数与y轴交点为：（0，），‎ 对于A，由直线与y轴交点可知，〈0，即a〉0，‎ 一次函数的图象中，y随x的增大而增大，所以，b〉0，‎ 因此，〈0，但由图可知，抛物线的对称轴〉0，矛盾，排除；‎ 对于B，由 ，得：＝0，△＝－4a2〈0，‎ 即直线与抛物线无交点，所以，B排除；‎ 对于D，因为抛物线必经过原点，所以，D排除；‎ 只有C符合。‎ ‎10、如图，在正方形中，是边上的一点，，，将正方形边沿折叠到，延长交于。连接，现在有如下四个结论：①；②；③∥；④‎ ‎ 其中结论正确的个数是（ ）‎ ‎ A、1 B、2‎ ‎ C、3 D、4‎ 答案：B 考点： 勾股定理，三角形的全等，应用数学知识解决问题的综合能力。‎ 解析：由题易知，则（HL），‎ ‎∴，，又 ‎∴，所以①正确；‎ 设，则，又， ∴，‎ ‎ ∴,，‎ 在中，由勾股定理可得 解得 ‎∴，又,∴不是等边三角形，所以②错误；‎ 由①可知和是对称型全等，则，又，‎ 则为直角三角形，∴，∴∥，∴③成立；‎ 由②可知∴，又，∴‎ ‎∴④错误，故正确结论为①③‎ 二、填空题；本大题共6小题，每小题4分，共24分。‎ ‎11、的相反数是 。‎ 答案：‎ 考点： 相反数。‎ 解析：＝3，‎ ‎3的相反数为－3‎ ‎12、分解因式： 。‎ 答案：‎ 考点：分解因式 解析：‎ ‎13、一组数据1，2，，5，8的平均数是5，则该组数据的中位数是 。‎ 答案：5‎ 考点： 数据的中位数，平均数。‎ 解析：，解得：x＝9，‎ 所以，数据为：1，2，5，8，9，中位数为5.‎ ‎14、已知、是方程的两根，则 。‎ 答案：6‎ 考点： 一元二次方程，韦达定理。‎ 解析：由韦达定理可得，，‎ ‎∴‎ ‎15、如图是一个多面体的表面展开图，如果面在前面，从左面看是面，那么从上面看是面 。（填字母）‎ 答案：C或E 考点： 长方体的展开图。‎ 解析：当C为底面时，F为前面，A为后面，B为左面，D为右面，上面是E；‎ C与E是相对面，B与D为相对面，A与F为相对面，E在底面时，则上面是C。‎ ‎16、正方形， ，，…按如图所示的方式放置，点，，，…和点，，，…分别在直线（）和轴上。已知，点，则的坐标是 。‎ 答案：‎ 考点：找规律，勾股定理。‎ 解析：由勾股定理，得：A1B1＝，‎ B1C1＝A1B1＝，C1的坐标为：C1（2，1），‎ B2C2＝A2B2＝2，C2的坐标为：C2（5，2），‎ B3C3＝A3B3＝4，C3的坐标为：C2（11，4），‎ B4C4＝A4B4＝8，C4的坐标为：C2（23，8），‎ B5C5＝A5B5＝16，C5的坐标为：C2（47，16），‎ 三、解答题：本大题共8小题，共66分，解答应写出文字说明，证明过程或验算步骤 ‎17、（本小题满分6分）解不等式，并把它的解集在数轴上表示出来。‎ ‎ ‎ ‎ ‎ 考点：一元一次不等 式 解析：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎18、（本小题满分6分）如图，在中，是边上的高，是边上的中线，且。求证：（1）点在的垂直平分线上；（2）‎ 考点： 中垂线的证明，等 边对等 角。‎ 解析：‎ 证明：（1）连接 ‎ ‎∵是边上的高 ‎ ‎∴ ‎ ‎∴‎ ‎∵是边上的中线 ‎ ‎∴ ‎ ‎∴ ‎ ‎∵ ‎ ‎∴ ‎ ‎∴点在线段的垂直平分线上 ‎ ‎（2）∵‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎19、（本小题满分6分）某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班，为了解学生对这四类兴趣班的喜爱情况，对学生进行了随机问卷调查（问卷调查表如图所示），将调查结果整理后绘制了一幅不完整的统计表 兴趣班 频数 频率 A ‎0.35‎ B ‎18‎ ‎0.30‎ C ‎15‎ D ‎6‎ 合计 ‎1‎ 最受欢迎兴趣班调查问卷 你好！这是一份关于你最喜欢的兴趣班问卷调查表，请在表格中选择一个（只能选一个）你最喜欢的兴趣班选项，在其后空格内打“√”谢谢你的合作 选项 兴趣班 请选择 A 绘画 B 音乐 C 舞蹈 D 跆拳道 ‎ 请你根据统计表中提供的信息回答下列问题：‎ ‎ （1）统计表中的 ， ；‎ ‎ （2）根据调查结果，请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数；‎ ‎ （3）王姝和李要选择参加兴趣班，若他们每人从、、、四类兴趣班中随机选取一类，请用画树状图或列表格的方法，求两人恰好选中同一类的概率。‎ 考点： 概率。‎ 解析：‎ 解：（1），；（2）最喜欢绘画兴趣的人数为700人 ‎ 王姝 李要 A B C D A AA AB AC AD B AB BB CB DB C AC BC CC DC D AD BD CD DD ‎ （3）‎ ‎ ‎ 所以，两人恰好选中同一类的概率为 ‎20、（本小题满分8分）如图，在平面直角坐标系中，一次函数的图像与反比例函数的图像在第二象限交于点，与轴交于点，点在轴上，满足条件：，且，点的坐标为，。‎ ‎ （1）求反比例函数的表达式；‎ ‎ （2）直接写出当时，的解集。‎ 考点： 反比函数和图象，三角形的全等，图象与不等 式。‎ 解析：‎ 解：（1）如图作轴于点 则 ‎∴‎ ‎∵点的坐标为 ‎∴‎ ‎∵‎ ‎∴，‎ 在和中 有 ‎∴≌‎ ‎∴，‎ ‎∴，即 ‎∴‎ ‎∴反比例函数解析式为 ‎（2）因为在第二象限中，点右侧一次函数的图像在反比例函数图像的下方 ‎ 所以当时，的解集为 ‎21、（本小题满分8分）攀枝花得天独厚，气候宜人，农产品资源极为丰富，其中晚熟芒果远销北上广等大城市。某水果店购进一批优质晚熟芒果，进价为10元/千克，售价不低于15元/千克，且不超过40元/每千克，根据销售情况，发现该芒果在一天内的销售量（千克）与该天的售价（元/千克）之间的数量满足如下表所示的一次函数关系。‎ 销售量（千克）‎ ‎…‎ ‎32.5‎ ‎35‎ ‎35.5‎ ‎38‎ ‎…‎ 售价（元/千克）‎ ‎…‎ ‎27.5‎ ‎25‎ ‎24.5‎ ‎22‎ ‎…‎ ‎（1）某天这种芒果售价为28元/千克。求当天该芒果的销售量 ‎（2）设某天销售这种芒果获利元，写出与售价之间的函数关系式。如果水果店该天获利400元，那么这天芒果的售价为多少元？‎ 考点： 待定系数法，一元二次方程，解应用题。‎ 解析：‎ 解：（1）设该一次函数解析式为 则 解得：‎ ‎∴（）‎ ‎∴当时，‎ ‎∴芒果售价为28元/千克时，当天该芒果的销售量为32千克 ‎ （2）由题易知 ‎ ‎ ‎ ‎ ‎ 当时，则 ‎ 整理得：‎ ‎ 解得：，‎ ‎ ∵‎ ‎ ∴‎ ‎ 所以这天芒果的售价为20元 ‎22、（本小题满分8分）‎ ‎ 如图1，有一个残缺的圆，请做出残缺圆的圆心（保留作图痕迹，不写做法）‎ ‎ 如图2，设是该残缺圆的直径，是圆上一点，的角平分线交于点，过点作的切线交的延长线于点。‎ ‎ （1）求证：；（2）若，，求残缺圆的半圆面积。‎ H ‎ 图1 图2‎ 考点： 垂径定理，切线的性质定理，矩形的判定。‎ 解析：‎ 解：图1做图题作法：‎ ‎①在残缺的圆上取两条不平行的弦和；‎ ‎②以点为圆心大于一半长为半径在两侧作圆弧；‎ ‎③以点为圆心，同样长的半径在两侧作圆弧与②中的 ‎ 圆弧交于，两点；‎ ‎④作直线即为线段的垂直平分线；‎ ‎⑤以同样的方法做线段的垂直平分线与直线交于点即为该残缺圆的圆心 ‎∴‎ ‎ 四边形为矩形 ‎∴‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎ 图2解答过程：‎ ‎ （1）证明：连接交于 ‎ ∵为的切线 ‎ ∴‎ ‎ ∵平分 ‎ ∴‎ ‎ ∵‎ ‎ ∴‎ ‎ ∴∥‎ ‎ ∴‎ ‎ （2）解：‎ ‎ ∵是的直径 ‎ ∴‎ ‎ ∵∥‎ ‎ ∴‎ ‎23、（本小题满分12分）已知抛物线的对称轴为直线，其图像与轴相交于、两点，与轴交于点。（1）求，的值；‎ ‎ （2）直线与轴交于点。‎ ‎ ①如图1，若∥轴，且与线段及抛物线分别相交于点、，点关于直线的对称点为，求四边形面积的最大值；‎ ‎ ②如图2，若直线与线段相交于点，当∽时，求直线的表达式。‎ H ‎ 图1 图2 ‎ 考点： 三角形的相似，抛物线的图象与性质。‎ 解析：‎ 解：（1）由题可知 ‎ 解得 ‎（2）①由题可知，‎ ‎ ∴‎ ‎ 由（1）可知，‎ ‎∴：‎ 设，则 ‎∴‎ ‎∴‎ ‎ ‎ ‎∴当时，四边形的面积最大，‎ 最大值为 ‎②由（1）可知 由∽可得 ‎∴ ∴‎ 由，可得 ‎∴‎ 作于点，设，则 ‎∴，‎ ‎∴‎ 即 解得 ‎∴ ∴：‎ ‎24、（本小题满分12分）在平面直角坐标系中，已知，动点在的图像上运动（不与重合），连接，过点作，交轴于点，连接。‎ ‎ （1）求线段长度的取值范围；‎ ‎ （2）试问：点运动过程中，是否问定值？如果是，求出该值；如果不是，请说明理由。‎ ‎ （3）当为等腰三角形时，求点的坐标。‎ 考点： 三角形的相似，三角函数，四点共圆。‎ 解析：‎ 解：（1）作，则 ‎∵点在的图像上 ‎∴，‎ ‎∵ ∴‎ ‎∴‎ ‎（2）法一：（共圆法）‎ ‎①当点在第三象限时，‎ 由 可得、、、四点共圆 ‎∴‎ ‎②当点在第一象的线段上时，‎ 由 可得、、、四点共圆 ‎∴，又此时 ‎∴‎ ‎③当点在第一象限的线段的延长线上时，‎ 由 可得 ‎∴、、、四点共圆 ‎∴‎ ‎ 法二：（相似法）‎ ‎ 如图设直线与交于点 ‎ ‎ ‎①当点在第三象限时，‎ 由 可得∽‎ ‎∴ ∴∽‎ ‎∴‎ ‎ ②当点在第一象限且点在延长线上时，‎ 由 可得 ‎∴∽ ∴ ‎ ‎∴∽ ∴‎ ‎③当点在第一象限且点在延长线上时，‎ 由 可得 ‎∴∽ ∴‎ ‎∴∽ ∴‎ ‎（3）设， 则：‎ ‎∵ ∴‎ ‎∴：‎ ‎∴‎ ‎∴，‎ ‎①当时， 则 整理得： 解得：‎ ‎∴， ‎ ‎②当时，则 整理得： ‎ 解得：或 当时，点与重合，舍去，‎ ‎∴ ∴‎ ‎③当时，‎ 则 整理得：‎ 解得：‎ ‎∴‎