数学文卷·2017届新疆库尔勒市第四中学高三上学期期中考试(2016
库尔勒市第四中学 2016-2017 学年(上)
高三年级期中 数学(文) (学科)试卷(问卷)
考试时间 120 分钟 班级: 姓名: 考号:
一、选择题:本题共 12 小题,每小题 5 分,共 60 分
1.设全集 U={1,2,3,4,5},集合 A={1,2},B={2,3,5},则(∁ UA)∪B=
( )
A.{3,5} B.{3,4,5} C.{2,3,4,5} D.{1,2,3,4}
2.若点(1,3)和(-4,-2)在直线 2x+y+m=0 的两侧,则 m 的取值范围
( )
A.m<-5 或 m>10 B.m=-5 或 m=10
C.-5
0,则 a 的
取值范围是( )
A.(2,+∞) B.(1,+∞) C.(-∞,-2) D.(-∞,-1)
二、填空题:本题共 4 小题,每小题 5 分,共 20 分
13.已知 0)(logloglog 237 x ,那么 x=_______
14.已知平面内有 A(-2,1),B(1,4),使AC
→
=1
2
CB
→
成立的点 C 坐标为__________.
15.若函数
)0(),(
)0(,32)( xxg
xxxf 是奇函数,则 g(x)=__________.
16.已知 p: 12 x ,q:(x-a)(x-a-4)>0,若 p 是 q 成立的充分不必要条
件,则实数 a 的取值范围是________.
三、解答题:本题共 6 题,17 题 10 分,18-22 题 12 分,共 70 分
17.(10 分)设△ABC 的内角 A,B,C 所对边的长分别是 a,b,c,且 b=3,
c=1,△ABC 的面积为 2,求 cos A 与 a 的值.
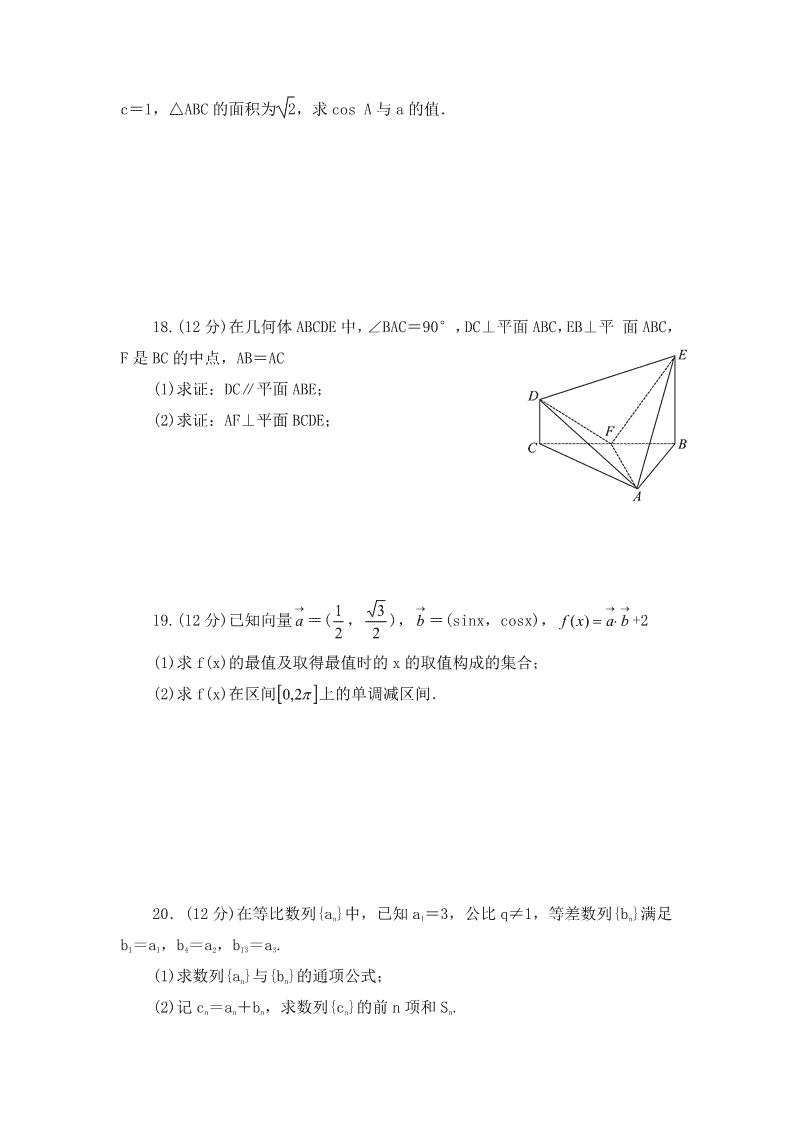
18.(12 分)在几何体 ABCDE 中,∠BAC=90°,DC⊥平面 ABC,EB⊥平 面 ABC,
F 是 BC 的中点,AB=AC
(1)求证:DC∥平面 ABE;
(2)求证:AF⊥平面 BCDE;
19.(12 分)已知向量
a =(
2
1 ,
2
3 ),
b =(sinx,cosx),
baxf )( +2
(1)求 f(x)的最值及取得最值时的 x 的取值构成的集合;
(2)求 f(x)在区间 2,0 上的单调减区间.
20.(12 分)在等比数列{an}中,已知 a1=3,公比 q≠1,等差数列{bn}满足
b1=a1,b4=a2,b13=a3.
(1)求数列{an}与{bn}的通项公式;
(2)记 cn=an+bn,求数列{cn}的前 n 项和 Sn.
21.(12 分)(1)求函数 y=x(a-2x)(x>0,a 为大于 2x 的常数)的最大值;
(2)已知 a>0,b>0,c>0,a2+b2+c2=4,求 ab+bc+ac 的最大值.
22.(12 分)已知 a,b 是实数,1 和-1 是函数 f(x)=x3+ax2+bx 的两个极
值点.
(1)求 a 和 b 的值;
(2)设函数 g(x)的导函数 )(xg =f(x)+2,求 g(x)的极值点.
高三文科数学期中考试卷答案
二、填空题(共 4 小题,每小题 5 分,共 20 分.将答案填在题中的横线上)
13.8. 14.(-1,2)
15.g(x)=2x+3 16.a<-6 或 a>1
三、解答题(本大题共 6 小题,共 70 分.)
17.【解】 由三角形面积公式,得1
2
×3×1·sin A= 2,故 sin A=2 2
3
.
因为 sin2A+cos2A=1, 所以 cos A=± 1-sin2A=± 1-8
9
=±1
3
.
①当 cos A=1
3时,由余弦定理得
a2=b2+c2-2bccosA=32+12-2×1×3×1
3
=8, 所以 a=2 2.
②当 cos A=-1
3
时,由余弦定理得
a2=b2+c2-2bccosA=32+12-2×1×3×-1
3
=12,所以 a=2 3.
18.证明:(1)∵DC⊥平面 ABC,EB⊥平面 ABC
∴DC∥EB,又∵DC⊄ 平面 ABE,EB⊂平面 ABE,
∴DC∥平面 ABE.
(2)DC⊥平面 ABC,∴DC⊥AF,
又∵AB=AC,F 为 BC 的中点
∴AF⊥BC,∴AF⊥平面 BCDE.
19.答案:(1)最大值 3,取最大值时 x 的集合为
zkkxx ,62
最小值 1,取最小值时 x 的集合为
zkkxx ,6
52
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C C D B A C A D C A A C
(2)单调减区间为
6
7,6
20.【解】 (1)设等比数列{an}的公比为 q,等差数列{bn}的公差为 d.
由已知,得
dq
dq
1233
333
2
⇒
dq
dq
41
1
2
⇒q=3 或 1(舍去).
所以 d=2,所以 an=3n,bn=2n+1.
(2)由题意,得 cn=an+bn=3n+(2n+1),
Sn=c1+c2+…+cn=(3+5+7+…+2n+1)+(3+32+…+3n)
=n(3+2n+1)
2
+
31
)31(3
n
=
2
3 1n
+n2+2n-3
2
.
21.解(1)∵x>0,a>2x,∴y=x(a-2x)=1
2
×2x(a-2x)≤
2
2
)2(2
2
1
xax =
8
2a ,
当且仅当 x=a
4
时取等号,故函数的最大值为
8
2a .
(2)∵a2+b2+c2=4,∴2ab+2bc+2ac≤(a2+b2)+(b2+c2)+(a2+c2)=2(a2
+b2+c2)=8,∴ab+bc+ac≤4,∴ab+bc+ac 的最大值为 4.
22.解:(1) baxxxf 23)( 2 .又 1 和-1 是函数 f(x)的两个极值点,
∴
023)1(
023)1(
baf
baf 解之得,a=0,b=-3.
(2)由(1)知, xxxf 3)( 3 , 23)( 3 xxxg .
由 0)( xg ,得 0)2()1( 2 xx ,
∴ 0)( xg 的根为 x=-2 或 1.
当 x<-2 时, 0)( xg ;
当-21 时, 0)( xg ,
故 1 不是 g(x)的极值点.
所以 g(x)的极小值点为-2,无极大值点.