八年级下数学课件《反比例函数的图像与性质》 (9)_苏科版

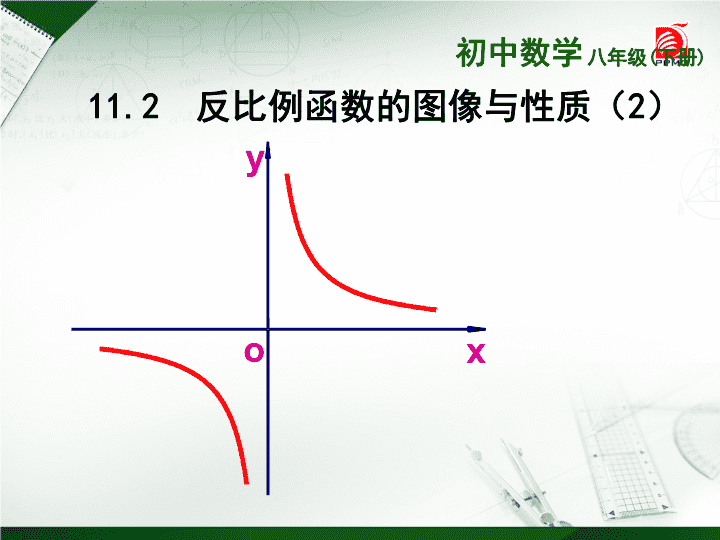
八年级下数学课件《反比例函数的图像与性质》 (9)_苏科版

学前回顾 1.下列关系式中y是x的反比例函数的是（　 　） A． B． C． D． x y 3 2  2 12  xy 4 xy  03 xy A 2. 反比例函数 图像是__________; 图像的两支分别在第_________ 象限． 反比例函数 的图象在第_______象限． 6y x  6y x   双曲线 一、三 二、四 3.我们从哪些方面研究一次函数y=kx+b(k ≠0) 的图像与性质 的？ 八年级(下册)初中数学 11.2　反比例函数的图像与性质（2） y xo 1y x  1y x   4y x  4y x   6y x  6y x   观察反比例数 、 、 、 、 的图像. 4 ＝y x 4 ＝－y x 6 ＝y x 6 ＝－y x 1 ＝ -y x 1 ＝y x ＝ ky x思考:反比例函数 （k为常数，k≠0）的图像有什么特征？ 问2：观察它们的形状、位置、增减性，你有什么结论？ 问1：若对这些函数进行分类，可分为几类？说明分类依据？ 探索 形状 所在象限 增减性 ( 0)ky k x   通过对上述图象的观察，完成下列表格： ( 0)ky k x   双曲线 双曲线 一、三象限 在每一象限内 y随x的增大而减小 在每一象限内 y随x的增大而增大 二、四象限 例1　已知反比例函数 的图像经过点 A（2，－ 4）. （1）求k的值； ＝ ky x 11.2　反比例函数的图像与性质（2） 变式1：反比例函数 的图像经过点（a，-3），求a。 题后小结 6 ＝y x 例1　已知反比例函数 的图像经过点 A（2，－ 4）. （2）这个函数的图像在哪几个象限？y随x的 增大怎样变化？ ＝ ky x 变式1：已知反比例函数 ,它的图像位于哪些象限？ 2 1 ＝ ay x 变式2：已知反比例函数 的图像位于二、四象限，求 a的范围。  4 ＝ ay x 变式3：已知反比例函数 的图像，当x›0，y随x的增 大而增大，求a的范围。  4 ＝ ay x 变式4：已知反比例函数 的图像在一、三象限，则一 次函数 不经过哪个象限？ ＝ ay x a＝ x-3y 例1　已知反比例函数 的图像经过点 A（2，－ 4）. ＝ ky x 11.2　反比例函数的图像与性质（2） （3）画出函数的图象； 画出函数的图象； 8y x   说说画反比例函数图 像的注意点 2 2 例1　已知反比例函数 的图像经过点 A（2，－ 4）. ＝ ky x （4）点B（ ，－16）、C（ － 3，5）在这 个函数的图像上吗？ 1 2 变式1：已知点A( 4 ，-2)在此函数的图像上吗？ 变式2：写出点A( 4 ，-2)关于原点的对称点A′的坐标——， 点A′也在此函数的图像上吗？ 变式3：点P( a ，b)是此函数的图像上的任意一点，则关于原点 的对称点P′也在此函数的图像上吗？ 如果将反比例函数的图象绕原点旋转１８０度， 你有什么发现？ 反比例函数的两支图像关于原点对称． 思考 函数 与 y=x 的图象有交点， （1）求k的取值范围____________; （2） 若一个交点A的坐标是（－3，－3）， 请直接写出两个图象的另一个交点B的坐标. ky x  拓展： 学科网 题后小结 探索 反比例函数图像是轴对称图形吗？ 如果是，对称轴有几条？ 形状 所在象限 增减性 对称性 ( 0)ky k x   归纳结论 ( 0)ky k x   双曲线 双曲线 一、三象限 在每一象限内 y随x的增大而减小 在每一象限内 y随x的增大而增大 既是轴对称图形， 又是中心对称图形 既是轴对称图形， 又是中心对称图形 二、四象限 例1　已知反比例函数 的图像经过点 A（2，－ 4）. ＝ ky x （5）点A（ －2 ，y1）、B（ － 1，y2）在此 函数的图像上，则y1 ____y2. 变式1：已知点A( －2 ，y1)、B( － 1，y2)在反比例函数 上,判断y1 与y2的大小.  2 1 ＝ ay x 变式2：已知点A( x1，y1)、B( x2，y2)在反比例函数 上,若x1›x2 , 判断y1 与y2的大小. 8 ＝-y x 课堂小结： 谈谈你这一节课有哪些收获． 11.2　反比例函数的图像与性质（2） 课堂小结： 1.反比例函数的图像是————． 11.2　反比例函数的图像与性质（2） 2.反比例函数图像的性质是怎样的？ 形状 位置 增减性 对称性 与坐标轴的交点 3.运用数形结合的思想解决问题。 2.一次函数y=kx－k 与反比例函数 y= 在同一直 角坐标系内的图象大致是（ ） x k D