2019年黄冈中考数学试题（解析版）

2019年黄冈中考数学试题（解析版）

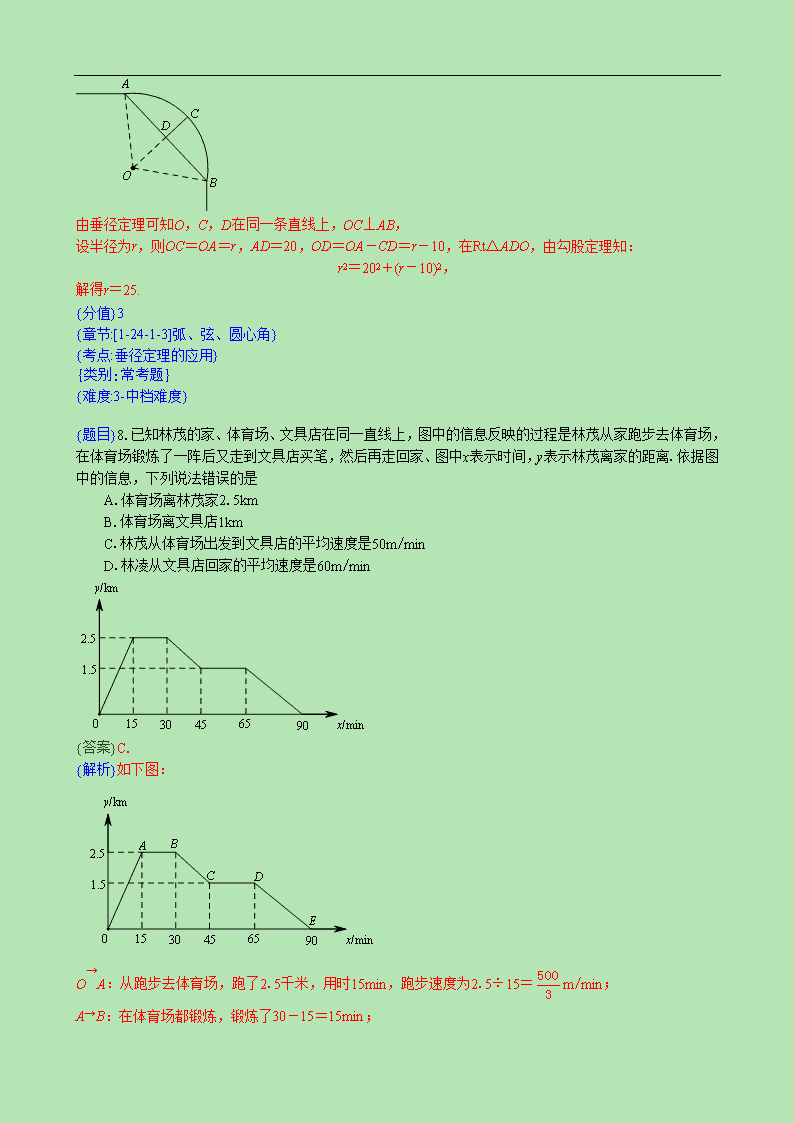
‎{来源}2019黄冈市中考数学 ‎{适用范围:3． 九年级}‎ ‎{标题}黄冈市二〇一九年初中学业水平考试 考试时间：120分钟 满分：150分 ‎{题型:1-选择题}一、选择题：本大题共 12 小题，每小题 4 分，合计48分． ‎ 一、选择题（本题共8小题，每小题3分，共24分.每小题给出的4个选项中，有且只有一个答案是正确的）‎ ‎{题目}1.－3的绝对值是 A.－3 B.－ C.3 D.±3‎ ‎{答案}C.‎ ‎{解析}本题考查了绝对值的概念，-3的绝对值是3.‎ ‎{分值}3‎ ‎{章节:[1-1-2-3]相反数}‎ ‎{考点:相反数的定义}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}2.为纪念中华人民共和国成立70周年，我市各中小学积极开展了以“祖国在我心中”为主题的各类教育活动，全市约有550000名中小学生参加.其中数据550000用科学记数法表示为 A.5.5×106 B.5.5×105 C.55×104 D.0.55×106‎ ‎{答案}B ‎{解析}本题考查了科学计数法，科学技术法的形式为a×10n（1≤│a│＜10），550000=5.5×105.‎ ‎{分值}3‎ ‎{章节:[1-1-5-2]科学计数法}‎ ‎{考点:将一个绝对值较大的数科学计数法}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}3.下列运算正确的是 A.a·a2＝a2 B.5a·5b＝5ab C.a5÷a3＝a2 D.2a＋3b＝5ab ‎{答案}C ‎{解析}本题考查了整式的运算，运算正确的选C.‎ ‎{分值}3‎ ‎{章节:[1-14-1]整式的乘法}‎ ‎{考点:合并同类项}‎ ‎{考点:单项式乘以单项式}‎ ‎{考点:单项式除法}‎ ‎{类别:常考题}‎ ‎{难度:2-最简}‎ ‎{题目}4.若x1，x2是一元一次方程x2－4x－5＝0的两根，则x1·x2的值为 A.－5 B.5 C.－4 D.4‎ ‎{答案}A ‎{解析}本题考查了一元二次方程根与系数的关系，选择A ‎{分值}3‎ ‎{章节:[1-21-3] 一元二次方程根与系数的关系}‎ ‎{考点:根与系数关系}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}5.已知点A的坐标为（2，1），将点A向下平移4个单位长度，得到的点A＇的坐标是 A.（6，1） B.（－2，1） C.（2，5） D.（2，－3）‎ ‎{答案}D ‎{解析}本题考查了坐标系中点的平移，正确答案选择D.‎ ‎{分值}3‎ ‎{章节:[1-7-4] 用坐标表示平移}‎ ‎{考点:坐标系内图形的平移}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}6.如图，是由棱长都相等的四个小正方体组成的几何体.该几何体的左视图是 ‎ ‎ ‎{答案}B ‎{解析}本题考查了三视图，选择B.‎ ‎{分值}3‎ ‎{章节:[1-29-2]三视图}‎ ‎{考点:简单组合体的三视图}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}7.如图，一条公路的转弯处是一段圆弧（），点O是这段弧所在圆的圆心，AB＝40m，点C是的中点，点D是AB的中点，且CD＝10m.则这段弯路所在圆的半径为 A.25m B.24m C.30m D.60m ‎{答案}A ‎{解析}本题考查了三视图，选择B.‎ ‎{解析}连接OD，‎ 由垂径定理可知O，C，D在同一条直线上，OC⊥AB，‎ 设半径为r，则OC＝OA＝r，AD＝20，OD＝OA－CD＝r－10，在Rt△ADO，由勾股定理知：‎ r2＝202＋(r－10)2，‎ 解得r＝25.‎ ‎{分值}3‎ ‎{章节:[1-24-1-3]弧、弦、圆心角}‎ ‎{考点:垂径定理的应用}‎ ‎{类别:常考题}‎ ‎{难度:3-中档难度}‎ ‎{题目}8.已知林茂的家、体育场、文具店在同一直线上，图中的信息反映的过程是林茂从家跑步去体育场，在体育场锻炼了一阵后又走到文具店买笔，然后再走回家、图中x表示时间，y表示林茂离家的距离.依据图中的信息，下列说法错误的是 A.体育场离林茂家2.5km B.体育场离文具店1km C.林茂从体育场出发到文具店的平均速度是50m/min D.林凌从文具店回家的平均速度是60m/min ‎{答案}C.‎ ‎{解析}如下图：‎ O→A：从跑步去体育场，跑了2.5千米，用时15min，跑步速度为2.5÷15＝m/min；‎ A→B：在体育场都锻炼，锻炼了30－15＝15min；‎ B→C：从体育场步行至文具店，步行2.5－15＝1km，用时45－30＝15min，说明体育场距离文具店1km，速度为1÷15＝m/min；‎ C→D：在文具店购买文具，用时65－45＝20min；‎ D→E：从文具店步行回家，步行1.5km，用时90－65＝25min，速度为1.5÷25＝60m/min.‎ ‎{分值}3‎ ‎{章节:[1-19-1-2] 函数的图象}‎ ‎{考点:函数的图象}‎ ‎{类别:常考题}‎ ‎{难度:3-中档难度}‎ 第Ⅱ卷（非选择题 共96分）‎ 二、填空题（本题共8小题，每小题3分，共24分）‎ ‎{题目}9.计算（）2＋1的结果是 .‎ ‎{答案}4.‎ ‎{解析}本题考查了数的运算，答案为4.‎ ‎{分值}3‎ ‎{章节:[1-6-1]平方根}‎ ‎{考点:平方根的定义}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}10.－x2y是 次单项式.‎ ‎{答案}三 ‎{解析}本题考查了单项式的命名.‎ ‎{分值}3‎ ‎{章节:[1-2-1]整式}‎ ‎{考点:单项式}‎ ‎{类别:常考题}‎ ‎{类别:易错题}‎ ‎{难度:1-最简单}‎ ‎{题目}11.分解因式3x2－27y2＝ .‎ ‎{答案}3(x＋3y)(x－3y).‎ ‎{解析}本题考查了因式分解.‎ ‎{分值}3‎ ‎{章节:[1-14-3]因式分解}‎ ‎{考点:因式分解－提公因式法}‎ ‎{考点:因式分解－平方差}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}12.一组数据1，7，8，5，4的中位数是a，则a的值是 .‎ ‎{答案}5‎ ‎{解析}本题考查了中位数的定义.‎ ‎{分值}3‎ ‎{章节:[1-20-1-2]中位数和众数}‎ ‎{考点:中位数}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}13.如图，直线AB∥CD，直线EC分别与AB，CD相交于点A，点C.AD平分∠BAC，已知∠ACD＝80°，则∠DAC的度数为 .‎ ‎{答案}50°‎ ‎{解析}本题考查了平分线和角平分线的概念.∵AB∥CD，∠ACD＝80°，∴∠BAC=180°-80°=100°，又∵AD平分∠BAC，∴∠DAC＝40°.‎ ‎{分值}3‎ ‎{章节:[1-5-3]平行线的性质}‎ ‎{考点:角平分线的定义}‎ ‎{考点:两直线平行同旁内角互补}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}14.用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，则这个圆锥的底面圆的面积为 .‎ ‎{答案}4π ‎{解析}由题可知，一个圆心角为120°，半径为6的扇形的弧长为×π×6＝4π，设圆锥的底面圆的半径为r，则2πr＝4π，r＝2，故面积4π.‎ ‎{章节:[1-24-4]弧长和扇形面积}‎ ‎{考点:圆锥侧面展开图}‎ ‎{类别:常考题}‎ ‎{类别:易错题}‎ ‎{难度:2-简单}‎ ‎{题目}15.如图，一直线经过原点O，且与反比例函数y＝(k＞0)相交于点A，点B，过点A作AC⊥y轴，垂足为C.连接BC.若△ABC的面积为8，则k＝ .‎ ‎{答案}8‎ ‎{解析}本题考查了反比例函数与一次函数的交点，反比例函数k的含义。‎ ‎∵过原点的直线与反比例函数交于A，B两点，‎ ‎∴可设A（xA，yA），B（－xA，－yA），‎ 则S△ABC＝×xA×2yA＝xAyA＝8＝k.‎ ‎{分值}3‎ ‎{章节:[1-26-1]反比例函数的图像和性质}‎ ‎{考点:反比例函数与一次函数的综合}‎ ‎{类别:常考题}‎ ‎{难度:3-中档难度}‎ ‎{题目}16.如图，AC，BD在AB的同侧，AC＝2，BD＝8，AB＝8.点M为AB的中点.若∠CMD＝120°，则CD的最大值是 .‎ ‎{答案}14‎ ‎{解析}将△ACM沿着CM翻折，使得A与A＇重合，连接CA＇，‎ 将△BDM沿着DM翻折，使得B与B＇重合，连接DB＇，‎ 连接AB，‎ 易求CA＇＝CA＝2，DB＇＝DB＝4，‎ 又∠A＇MB＇＝60°，A＇M＝B＇M，‎ ‎∴△A＇B＇M为等边三角形，‎ 可得A＇B＇＝AM＝2，‎ 易知CD≤CA＇＋A＇B＇＋B＇D，‎ ‎∴当C，A＇，B＇，D共线时，CD取得最大值.‎ ‎{分值}3‎ ‎{章节:[1-13-1-1]轴对称}‎ ‎{考点:全等三角形的应用}‎ ‎{难度:5-高难度}‎ ‎{类别:高度原创}‎ ‎{类别:思想方法}‎ 三、解答题（本题共9题，满分72分）‎ ‎{题目}17.（本题满分6分）先化简，再求值.‎ ‎÷，其中a＝，b＝1.‎ ‎{答案}5ab，5.‎ ‎{解析}本题考查了分式的运算.原式＝×ab(a＋b)＝5ab.‎ 当a＝，b＝1时，原式＝5ab＝5.‎ ‎{分值}6‎ ‎{章节:[1-15-2-2]分式的加减}‎ ‎{考点:分式的混合运算}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}18.（本题满分6分）解不等式组.‎ ‎{答案}－1＜x≤2.‎ ‎{解析}解：由①得：x＞－1，‎ 由②得：x≤2，‎ ‎∴此不等式组的解集为：－1＜x≤2.‎ ‎{分值}6‎ ‎{章节:[1-9-3]一元一次不等式组}‎ ‎{考点:解一元一次不等式组}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}19.（本题满分6分）如图，ABCD是正方形，E是CD边上任意一点，连接AE，作BF⊥AE，DG⊥AE，垂足分别为F，G.求证：BF－DG＝FG.‎ ‎{答案}见解析.‎ ‎{解析}本题考查了三角形的全等.‎ 证明：在△ABF和△DAG中，‎ ‎∵BF⊥AE，DG⊥AE，‎ ‎∴∠AFB＝∠DGA＝90°.‎ 又∠DAG＋∠FAB＝∠DAG＋∠ADG＝90°，‎ ‎∴∠FAB＝∠GDA.‎ 又AB＝AD，∴ABF≌DAG.‎ ‎∴BF＝AG，AF＝DG.‎ ‎∴BF－DG＝AG－AF＝FG.‎ ‎{分值}6‎ ‎{章节:[1-12-2]三角形全等的判定}‎ ‎{考点:全等三角形的判定ASA,AAS}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}20.（本题满分7分）为了对学生进行革命传统教育，红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发，步行4000米到达烈士纪念馆.学校要求九（1‎ ‎）班提前到达目的地，做好活动的准备工作.行走过程中，九（1）班步行的平均速度是其他班的1.25倍，结果比其他班提前10分钟到达.分别求九（l）班、其他班步行的平均速度.‎ ‎{答案}九（1）班的平均速度为100米/分，其他班的平均速度为80米/分.‎ ‎{解析}本题考查了分式方程的应用. ：设其他班的平均速度为x米/分，则九（1）班平均速度为1.25x米/分，已题意得：‎ ‎－＝10，‎ 解得：x＝80.‎ 经检验，x＝80是所列方程的解且符合实际题意.‎ 此时，1.25x＝1.25×80＝100.‎ 答：九（1）班的平均速度为100米/分，其他班的平均速度为80米/分.‎ ‎{分值}7‎ ‎{章节:[1-15-3]分式方程}‎ ‎{考点:分式方程的应用（行程问题）}‎ ‎{类别:常考题}‎ ‎{难度:3-中档难度}‎ ‎{题目}21.（本题满分8分）某校开发了“书画、器乐、戏曲、棋类”四大类兴趣课程。为了解全校学生对每类课程的选择情况，随机抽取了若干名学生进行调查（每人必选且只能选一类）.现将调查结果绘制成如下两幅不完整的统计图：‎ ‎（1）本次随机调查了多少名学生？‎ ‎（2）补全条形统计图中“书画”、“戏曲”的空缺部分；‎ ‎（3）若该校共有1200名学生，请估计全校学生选择“戏曲”类的人数；‎ ‎（4）学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”.用树形图或列表法求出恰好抽到“器乐”和“戏曲”类的概率（书画、器乐、戏曲、棋类可分别用字母A，B，C，D表示）‎ ‎{答案}解：（1）由棋类可知：30÷15%＝200，故本次随机调查了200名学生.‎ ‎（2）书画50人，戏曲40人（见图）.‎ ‎（3）×1200＝240人 ‎（4）图表略.答案（注：过程分析1分；正确结果1分）.‎ ‎{解析}（1）由器乐的人数及其所占百分比可得总人数； （2‎ ‎）总人数乘以书画对应百分比求得其人数，再根据各类型人数之和等于总人数求得戏曲人数，从而补全图形； （3）利用样本估计总体思想求解可得； （4）列表或树状图将所有等可能的结果列举出来后利用概率公式求解即可．‎ ‎{分值}8‎ ‎{章节:[1-25-1-2]概率}‎ ‎{考点:用样本估计总体}‎ ‎{考点:频数（率）分布直方图}‎ ‎{考点:扇形统计图}‎ ‎{考点:条形统计图}‎ ‎{考点:概率的意义}‎ ‎{类别:常考题}‎ ‎{难度:3-中档难度}‎ ‎{题目}22.（本题满分7分）如图，两座建筑物的水平距离BC为40m，从A点测得D点的俯角α为45°，测得C点的俯角β为60°.求这两座建筑物AB，CD的高度.（结果保留小数成后一位，≈1.414，≈1.732.）‎ ‎{答案}解：延长CD交过A点的水平线于点M，则∠AMC＝90°，AM＝BC＝40，‎ 在Rt△ADM中，tanα＝，∴DM＝AM×tanα＝40×tan45°＝40，‎ 在Rt△ACM中，tanβ＝，∴DM＝AM×tanβ＝40×tan60°＝40，‎ ‎∵AB＝CM，∴AB＝40≈40×1.732≈69.3m，‎ 又CD＝CM－DM＝40－40≈40×1.732－40≈29.3m.‎ 答：建筑物AB的高度约为69.3m，建筑物CD的高度约为29.3m.‎ ‎{解析}本题考查了解直角三角形及其应用.‎ ‎{分值}7‎ ‎{章节:[1-28-1-2]解直角三角形}‎ ‎{考点:解直角三角形的应用－仰角}‎ ‎{类别:常考题}‎ ‎{难度:3-中档难度}‎ ‎{题目}23.(本题满分8分)如图，Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O交AB于点D过点D作⊙O的切线交BC于点E，连接OE.‎ ‎(1)求证：△DBE是等腰三角形；‎ ‎(2)求证：△COE∽△CAB.‎ ‎{答案}（1）证明：连接OD，‎ ‎∵DE切⊙O于点D，∴OD⊥AB，∴∠ADO＋∠BDE＝90°，‎ ‎∵∠ACB＝90°，∴∠BAC＋∠ABC＝90°，‎ 又∵OA＝OD，∴∠OAD＝∠ADO，‎ ‎∴∠ABC＝∠DBE，‎ ‎∴△DBE是等腰三角形;‎ ‎（2）证明：在Rt△OCE与Rt△ODE中，，‎ ‎∴Rt△OCE≌Rt△ODE（HL），‎ ‎∴∠OEC＝∠OED，‎ ‎∵∠DEC＝∠DBE＋∠ABC＝2∠DBE，‎ 又∠DEC＝∠OEC＋∠OED＝2∠OEC，‎ ‎∴∠OEC＝∠ABC，又∠ACB＝∠OCE＝90°，‎ ‎∴△COE∽△CAB.‎ ‎{解析}本题考查了等腰三角形与直角三角形；圆的有关概念及性质；图形的相似．‎ ‎{分值}8‎ ‎{考点:相似三角形的性质}‎ ‎{考点:圆的其它综合题}‎ ‎{类别:常考题}‎ ‎{难度:3-中档难度}‎ ‎{题目}24.(本题满分10分)某县积极响应市政府加大产业扶贫力度的号召，决定成立草莓产销合作社，负责扶贫对象户种植草莓的技术指导和统一销售，所获利润年底分红.经市场调研发现，草莓销售单价y(万元)与产量x(吨)之间的关系如图所示(0≤x≤100)，已知草莓的产销投人总成本p(万元)与产量x(吨)之间满足P＝x＋1.‎ ‎(1)直接写出草莓销售单价y(万元)与产量x(吨)之间的函数关系式；‎ ‎(2)求该合作社所获利润w(万元)与产量x(吨)之间的函数关系式；‎ ‎(3)为提高农民种植草莓的积极性，合作社决定按0.3万元/吨的标准奖励扶贫对象种植户，为确保合作社所获利润w＇不低于55万元，产量至少要达到多少吨?‎ ‎{答案}（1）依题意可知：，‎ ‎（2）由题w＝xy－p,‎ ‎①当0≤x≤30时，w＝xy－p＝2.4x－x－1＝0.4x－1；‎ ‎②当30≤x≤70时，w＝xy－p＝(－0.01x＋2.7)x－x－1＝－0.01x2＋1.7x－1；‎ ‎③当70≤x≤100时，w＝xy－p＝2x－x－1＝x－1；‎ 综上，；‎ ‎（3）由题w＇＝(y－0.3)x－p,w＇≥55,‎ ‎①当0≤x≤30时，w＇＝(y－0.3)x－p＝2.1x－x－1＝1.1x－1，此时w＇≤32；‎ ‎②当30≤x≤70时，w＇＝(y－0.3)y－p＝(－0.01x＋2.7－0.3)x－x－1＝－0.01x2＋1.4x－1，‎ ‎－0.01＜0,x对＝70，∴w＇≤48，‎ ‎③当70≤x≤100时，w＝(y－0.3)x－p＝1.7x－x－1＝0.7x－1,‎ ‎0.7x－1≥55,解得x≥80，‎ ‎∴获利润w＇不低于55万元，产量至少要达到80吨.‎ ‎{解析}本题考查了一次函数、二次函数及其应用.‎ ‎{分值}10‎ ‎{章节:[1-22-3]实际问题与二次函数}‎ ‎{考点:商品利润问题}‎ ‎{类别:常考题}‎ ‎{难度:3-中档难度}‎ ‎{题目}25.(本题满分14分)如图①在平面直角坐标系xOy中，已知A(－2，2)，B(－2，0)，C(0，2)，D(2，0)四点，动点M以每秒个单位长度的速度沿B→C→D运动(M不与点B、点D重合)，设运动时间为t(秒).‎ ‎(1)求经过A、C、D三点的抛物线的解析式；‎ ‎(2)点P在(1)中的抛物线上，当M为BC的中点时，若△PAM≌△PBM，求点P的坐标；‎ ‎(3)当M在CD上运动时，如图②.过点M作MF⊥x轴，垂足为F，ME⊥AB，垂足为E.设矩形MEBF与△BCD重叠部分的面积为S，求S与t的函数关系式，并求出S的最大值；‎ ‎(4)点Q为x轴上一点，直线AQ与直线BC交于点H，与y轴交于点K.是否存在点Q，使得△HOK为等腰三角形?若存在，直接写出符合条件的所有Q点的坐标；若不存在，请说明理由.‎ ‎{答案}（1）y＝－x2－x＋2；‎ ‎(2)P1(－1＋，1)，P2(－1－，1)；‎ 提示：∵△PAM≌△PBM，‎ ‎∴PA＝PB，MA＝MB，‎ ‎∴点P为AB的垂直平分线与抛物线的交点.‎ ‎∵AB＝2，‎ ‎∴点P的纵坐标为1，‎ 令y＝－x2－x＋2，解得x1＝－1＋，x2＝－1－.‎ ‎∴P1(－1＋，1)，P2(－1－，1)；‎ ‎（3）易求BC的解析式为y＝x＋2,‎ ‎∵M在CD上运动，‎ ‎∴2≤t≤4，且CM＝t－2，‎ ‎∴DM＝CD－CM＝2－（t－2）＝4－t，‎ 可得MF＝DF＝4－t，∴M(t－2，4－t),E(－2，4－t),G(2－t，4－t),‎ ‎∴MG＝2－t－(4－t)＝2t－4，BF＝2＋t－2＝t,‎ ‎∴S＝(MG＋BF)×MF÷2＝－t2＋8t－8，‎ ‎∵－＜0，t对＝＜4，‎ ‎∴当t＝，S取得最大值，最大值为；‎ ‎（4）存在点Q，其坐标是Q1（－2－，0），Q2（－2－2，0），Q3（－2＋，0），Q4（－2＋2，0）.‎ 提示：‎ 易求，直线BC：y＝x＋2，‎ 设直线AH：y＝mx＋n，过点A易知n＝2m＋2，m≠1，若m=1则AH∥BC无交点.‎ 联立，求得H（，），也即H（，），‎ 则K（0，n），即K（0，2m＋2），Q(－，0)，设xQ＝－＝－，‎ 于是有：‎ OH2＝，OK2＝4（m＋1）2，‎ KH2＝＋（－2m－2）2＝＋=，‎ ‎∵△HOK是等腰三角形，‎ ‎∴分以下三种情况讨论：‎ ‎①当OH＝OK时，即＝4（m＋1）2，‎ ½4m2＋4＝4(m＋1)2(m－1)2½m2＋1＝(m2－1)2½m4－3m2＝0½m2(m2－3)＝0，‎ 解得m1＝，m2＝－，‎ 当m1＝时，xQ＝－＝－2－，‎ 当m2＝－时，xQ＝－＝－2＋；‎ 即Q1（－2－，0），Q2（－2＋，0）；‎ ‎②当OH＝KH，即＝½4m2＋4＝4m2(m2＋1)½4m4＝4，m4＝1，‎ 解得m1＝1（舍），m2＝－1，‎ 当m2＝－1时，xQ＝－＝0与原点重合，舍去；‎ ‎③当OK＝KH，即4（m＋1）2＝，‎ ½4（m＋1）2（m－1）2＝4m2(m2＋1)½m4－2m2＋1＝m4＋m2½m2＝,‎ 解得m1＝，m2＝－，当m1＝时，xQ＝－＝－2－2，‎ 当m2＝－时，xQ＝－＝－2＋2；Q3（－2－2，0），Q4（－2＋2，0）.‎ ‎{解析}本题考查了本题考查二次函数综合；熟练应用待定系数法求函数解析式，掌握三角形全等的性质，‎ 直线交点的求法是解题的关键．‎ ‎{分值}14‎ ‎{章节:[1-22-2]二次函数与一元二次方程}‎ ‎{考点:二次函数y＝ax2+bx+c的性质}‎ ‎{考点:抛物线与一元二次方程的关系}‎ ‎{考点:二次函数中讨论等腰三角形}‎ ‎{考点:几何综合}‎ ‎{难度:5-高难度}‎ ‎{类别:高度原创}‎ ‎{类别:思想方法}‎