- 2021-05-31 发布 |
- 37.5 KB |
- 51页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学等腰三角形专题复习
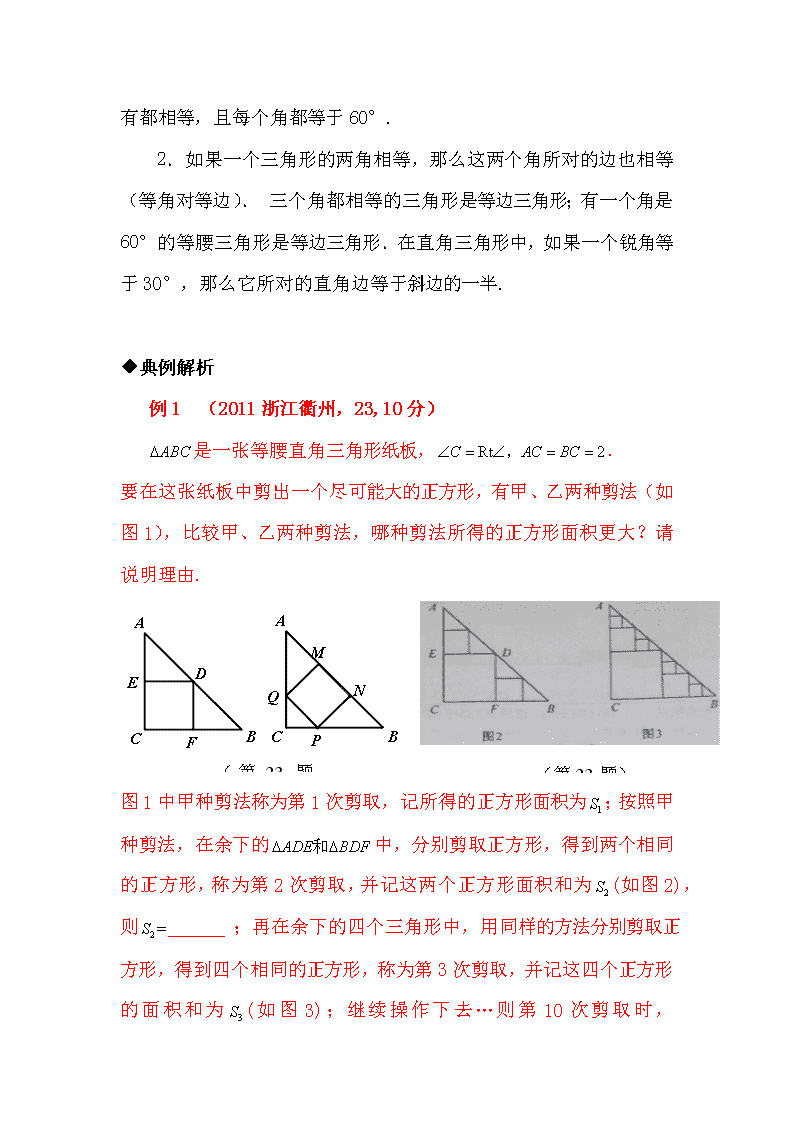
(备战中考)江苏省2012年中考数学深度复习讲义 (教案+中考真题+模拟试题+单元测试) 等腰三角形 ◆考点聚焦 1.等腰三角形的判定与性质. 2.等边三角形的判定与性质. 3.运用等腰三角形、等边三角形的判定与性质解决有关计算与证明问题. ◆备考后法 1.运用三角形不等关系,结合等腰三角形的判定与性质解决等腰三角形中高、边、角的计算问题,并要注意分类讨论. 2.要正确辨析等腰三角形的判定与性质. 3.能熟练运用等腰三角形、方程(组)、函数等知识综合解决实际问题. ◆识记巩固 1.等腰三角形的性质定理及推论:____________________________. 2.等腰三角形的判定定理及推论:____________________________. 识记巩固参考答案: 1.等腰三角形的两个底角相等(等边对等角);等腰三角形的顶角平分线平分底边并且垂直于底边(三线合一); 等边三角形的各有都相等,且每个角都等于60°. 2.如果一个三角形的两角相等,那么这两个角所对的边也相等(等角对等边).三个角都相等的三角形是等边三角形;有一个角是60°的等腰三角形是等边三角形.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. ◆典例解析 例1 (2011浙江衢州,23,10分) 是一张等腰直角三角形纸板,. 要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积更大?请说明理由. (第23题) (第23题图1) 图1中甲种剪法称为第1次剪取,记所得的正方形面积为;按照甲种剪法,在余下的中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为(如图2),则 ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为(如图3);继续操作下去…则第10次剪取时, . 求第10次剪取后,余下的所有小三角形的面积和. 【答案】(1)解法1:如图甲,由题意得.如图乙,设,则由题意,得 又 甲种剪法所得的正方形的面积更大 说明:图甲可另解为:由题意得点D、E、F分别为的中点, 解法2:如图甲,由题意得 如图乙,设 甲种剪法所得的正方形的面积更大 (2) (3) (3)解法1:探索规律可知:‘ 剩余三角形的面积和为: 解法2:由题意可知, 第一次剪取后剩余三角形面积和为 第二次剪取后剩余三角形面积和为 第三次剪取后剩余三角形面积和为 …中.考.资.源.网 第十次剪取后剩余三角形面积和为 例 2 如图,△ABC中,E,F分别是AB,AC上的点.①AD平分∠BAC;②DE⊥AB,DF⊥AC;③AD⊥EF.以此三个中的两个为条件,另一个为结论,可构成三个命题,即:①②③;①③②;②③①. (1)试判断上述三个命题是否正确(直接作答); (2)请证明你认为正确的命题. 解析 (1)①②③正确;①③②错误;②③①正确. (2)先证①②③,如图1. ∵AD平分∠BAC,DE⊥AB,DF⊥AC, ∴DE=DF,∠AED=∠AFD=90°. 在Rt△AED和Rt△AFD中, ∴△AED≌△AFD(HL). ∴AE=AF. ∴△AEF是等腰三角形,∴AD⊥EF. 再证②③①. 图1 图2 图3 方法一:如图2,DE⊥AB,EF⊥AD,DF⊥AC.[来源:中.考.资.源.网WWW.ZK5U.COM] 易证△DEH∽△DAE,△DFH∽△DAF. ∴, ∴DE2=AD·DH,DF2=DH·AD. ∴DE2=DF2,∴DE=DF,∴AD平分∠BAC. 方法二:如图3,取AD的中点O,连结EO,FO. ∵DE⊥AB,DF⊥AC, ∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线. ∴OE=AD,OF=AD. 即O点到A,E,D,F的距离相等. ∴A,E,D,F四点在以O为圆心,AD为半径的圆上,AD是直径,EF是⊙O的弦,而EF⊥AD,∴AD平分,即. ∴∠DAE=∠DAF,即AD平分∠BAC. 点评 本题是义务教育课程标准实验教科书数学(人教版) 八年级上第111页拓广探索题的变式与拓展,该例在教材中多次以不同形式出现,八年级(上)(人教版)第150页第13题,第158页第11题.因此,在九年级的学习过程中一定要重视教材中的典型例题,习题,想一想这些题还可以进行怎样的变式,与前后的知识与方法有什么联系,还可以得到什么结论等.这样可以不断提高自己的综合解题能力. 2011年真题 一、选择题 1. (2011浙江省舟山,7,3分)如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( ) (A) (B) (C) (D) (第7题) 【答案】B 2. (2011四川南充市,10,3分)如图,⊿ABC和⊿CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=;②S⊿ABC+S⊿CDE≧S⊿ACE ;③BM⊥DM;④BM=DM.正确结论的个数是( ) (A)1个 (B)2个 (C)3个 (D)4个 【答案】D 3. (2011浙江义乌,10,3分)如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°, 四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交 CE于点G,连结BE. 下列结论中: ① CE=BD; ② △ADC是等腰直角三角形; ③ ∠ADB=∠AEB; ④ CD·AE=EF·CG; 一定正确的结论有 A B C D E F G A.1个 B.2个 C.3个 D.4个 【答案】D 4. (2011台湾全区,30)如图(十三),ΔABC中,以B为圆心,长为半径画弧,分别交、 于D、E两点,并连接、.若∠A=30∘,=,则∠BDE的度数为何? A. 45 B. 52.5 C. 67.5 D. 75 【答案】C 5. (2011台湾全区,34)如图(十六),有两全等的正三角形ABC、DEF,且D、A分别为△ABC、△DEF 的重心.固定D点,将△DEF逆时针旋转,使得A落在上,如图(十七)所示.求图(十六)与图(十 七)中,两个三角形重迭区域的面积比为何? A.2:1 B. 3:2 C. 4:3 D. 5:4 【答案】C 6. (2011山东济宁,3,3分)如果一个等腰三角形的两边长分别是5cm和6cm,那么此三角形的周长是 A.15cm B.16cm C.17cm D.16cm或17cm 【答案】D 7. (2011四川凉山州,8,4分)如图,在中,,,点为的中点,,垂足为点,则等于( ) A. B. C. D. 中.考.资.源.网 【答案】C 8. 二、填空题 1. (2011山东滨州,15,4分)边长为6cm的等边三角形中,其一边上高的长度为________. 【答案】cm 2. (2011山东烟台,14,4分)等腰三角形的周长为14,其一边长为4,那么,它的底边为 . 【答案】4或6[来源:中.考.资.源.网] 3. (2011浙江杭州,16,4)在等腰Rt△ABC中,∠C=90°,AC=1,过点C作直线l∥AB,F是l上的一点,且AB=AF,则点F到直线BC的距离为 . 【答案】 4. (2011浙江台州,14,5分)已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,DBˊ, EBˊ分别交边AC于点F,G,若∠ADF=80º ,则∠EGC的度数为 【答案】80º 5. (2011浙江省嘉兴,14,5分)如图,在△ABC中,AB=AC,,则△ABC的外角∠BCD= °. (第14题) 【答案】110 6. (2011湖南邵阳,11,3分)如图(四)所示,在△ABC中,AB=AC,∠B=50°,则∠A=_______。 【答案】80°。提示:∠A=180°-2×50°=80°。 7. (2011山东济宁,15,3分)如图,等边三角形ABC中,D、E分别为AB、BC边上的两个动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则 . 第15题 D 【答案】 8. (2011湖南怀化,13,3分)如图6,在△ABC中,AB=AC,∠BAC的角平分线交BC边于点D,AB=5,BC=6,则AD=__________________. 【答案】4 9. (2011四川乐山16,3分)如图,已知∠AOB=,在射线OA、OB上分别取点OA=OB,连结AB,在BA、BB上分别取点A、B,使B B= B A,连结A B…按此规律上去,记∠A B B=,∠,…,∠ 则⑴= ; ⑵ = 。 【答案】⑴ ⑵ 10.(2011湖南邵阳,11,3分)如图(四)所示,在△ABC中,AB=AC,∠B=50°,则∠A=_______。 【答案】80°。 11. (2011贵州贵阳,15,4分)如图,已知等腰Rt△ABC的直角边长为1,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推直到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为______. (第15题图) 【答案】 12. (2011广东茂名,14,3分)如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 度. 【答案】15 三、解答题 1. (2011广东东莞,21,9分)如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止.不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2). (1)问:始终与△AGC相似的三角形有 及 ; (2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由); (3)问:当x为何值时,△AGH是等腰三角形? 【解】(1)△HGA及△HAB; (2)由(1)可知△AGC∽△HAB ∴,即, 所以, (3)当CG<时,∠GAC=∠H<∠HAC,∴AC<CH ∵AG<AC,∴AG<GH 又AH>AG,AH>GH 此时,△AGH不可能是等腰三角形; 当CG=时,G为BC的中点,H与C重合,△AGH是等腰三角形; 此时,GC=,即x= 当CG>时,由(1)可知△AGC∽△HGA 所以,若△AGH必是等腰三角形,只可能存在AG=AH 若AG=AH,则AC=CG,此时x=9 综上,当x=9或时,△AGH是等腰三角形. 2. (2011山东德州19,8分)如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O. (1)求证AD=AE;(2) 连接OA,BC,试判断直线OA,BC的关系并说明理由. A B C E D O 【答案】A B E C D O (1)证明:在△ACD与△ABE中, ∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC, ∴ △ACD≌△ABE.…………………… 3分 ∴ AD=AE. ……………………4分 (2) 互相垂直 ……………………5分 在Rt△ADO与△AEO中, ∵OA=OA,AD=AE, ∴ △ADO≌△AEO. ……………………………………6分 ∴ ∠DAO=∠EAO. 即OA是∠BAC的平分线. ………………………………………7分 又∵AB=AC, ∴ OA⊥BC. ………………………………………8分 3. (2011山东日照,23,10分)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA. (1)求证:DE平分∠BDC; (2)若点M在DE上,且DC=DM, 求证: ME=BD. 【答案】(1)在等腰直角△ABC中, ∵∠CAD=∠CBD=15o, ∴∠BAD=∠ABD=45o-15o=30o, ∴BD=AD,∴△BDC≌△ADC, ∴∠DCA=∠DCB=45o. 由∠BDM=∠ABD+∠BAD=30o+30o=60o, ∠EDC=∠DAC+∠DCA=15o+45o=60o, ∴∠BDM=∠EDC, ∴DE平分∠BDC; (2)如图,连接MC, ∵DC=DM,且∠MDC=60°, ∴△MDC是等边三角形,即CM=CD. [来源:中.考.资.源.网] 又∵∠EMC=180°-∠DMC=180°-60°=120°, ∠ADC=180°-∠MDC=180°-60°=120°, ∴∠EMC=∠ADC. 又∵CE=CA, ∴∠DAC=∠CEM=15°,∴△ADC≌△EMC,∴ME=AD=DB. 4. (2011湖北鄂州,18,7分)如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长. 第18题图 B A E D F C 【答案】连结BD,证△BED≌△CFD和△AED≌△BFD,求得EF=5 5. (2011浙江衢州,23,10分)是一张等腰直角三角形纸板,. 要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积更大?请说明理由. (第23题) (第23题图1) 图1中甲种剪法称为第1次剪取,记所得的正方形面积为;按照甲种剪法,在余下的中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为(如图2),则 ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为(如图3);继续操作下去…则第10次剪取时, . 求第10次剪取后,余下的所有小三角形的面积和. 【答案】(1)解法1:如图甲,由题意得.如图乙,设,则由题意,得 又 甲种剪法所得的正方形的面积更大 说明:图甲可另解为:由题意得点D、E、F分别为的中点, 解法2:如图甲,由题意得 如图乙,设 甲种剪法所得的正方形的面积更大 (2) (3) (3)解法1:探索规律可知:‘ 剩余三角形的面积和为: 解法2:由题意可知, 第一次剪取后剩余三角形面积和为中.考.资.源.网 第二次剪取后剩余三角形面积和为 第三次剪取后剩余三角形面积和为 … 第十次剪取后剩余三角形面积和为 6. (2011浙江绍兴,23,12分)数学课上,李老师出示了如下框中的题目. 小敏与同桌小聪讨论后,进行了如下解答: (1)特殊情况,探索结论 当点为的中点时,如图1,确定线段与的大小关系,请你直接写出结论: (填“>”,“<”或“=”). 第25题图2 第25题图1 (2)特例启发,解答题目 解:题目中,与的大小关系是: (填“>”,“<”或“=”).理由如下:如图2,过点作,交于点. (请你完成以下解答过程) (3)拓展结论,设计新题 在等边三角形中,点在直线上,点在直线上,且.若的边长为1,,求的长(请你直接写出结果). 【答案】(1)= . (2)=. 方法一:如图,等边三角形中, 中.考.资.源.网 是等边三角形, 又 .中.考.资.源.网 方法二:在等边三角形中,[来源:中.考.资.源.网] 而由是正三角形可得 (3)1或3. 7. (2011浙江台州,23,12分)如图1,过△ABC的顶点A分别做对边BC上的高AD和中线AE,点D是垂足,点E是BC中点,规定。特别的,当点D重合时,规定。另外。对、作类似的规定。 (1)如图2,已知在Rt△ABC中,∠A=30º,求、; (2)在每个小正方形边长为1的4×4方格纸上,画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且,面积也为2; (3)判断下列三个命题的真假。(真命题打√,假命题打×) ① 若△ABC中,,则△ABC为锐角三角形;( ) ② 若△ABC中,,则△ABC为直角三角形;( ) ③ 若△ABC中,,则△ABC为钝角三角形;( ) 【答案】解:(1)如图,作CD⊥AB,垂足为D,作中线CE、AF。 ∴=1 ∵ Rt△ABC中,∠CAB=30º, ∴ AE=CE=BE ,∠CEB=60º, ∴△CEB是正三角形, ∵ CD⊥AB ∴ AE=2DE ∴=; ∴=1,=; (2)如图所示: (3)①×;②√;③√。 8. (2011浙江义乌,23,10分)如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180 °),得到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F. (1) 如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 ▲ 关系(填“相似”或“全等”),并说明理由; (2)如图2,设∠ABP=β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由; (3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面 积为S,求S关于x的函数关系 图1 图2 图3 P B1 FM A DO EC C B A1 P B1 FM A DO EC C B A1 P B1 A DO C B A1 【答案】(1) 相似 由题意得:∠APA1=∠BPB1=α AP= A1P BP=B1P 则 ∠PAA1 =∠PBB1 = ∵∠PBB1 =∠EBF ∴∠PAE=∠EBF 又∵∠BEF=∠AEP ∴△BEF ∽△AEP (2)存在,理由如下: 易得:△BEF ∽△AEP 若要使得△BEF≌△AEP,只需要满足BE=AE即可 ∴∠BAE=∠ABE ∵∠BAC=60° ∴∠BAE= ∵∠ABE=β ∠BAE=∠ABE ∴ 即α=2β+60° (3)连结BD,交A1B1于点G, 过点A1作A1H⊥AC于点H. P B1 A DO C B A1 H G ∵∠B1 A1P=∠A1PA=60° ∴A1B1∥AC 由题意得:AP= A1 P ∠A=60° ∴△PAA1是等边三角形 ∴A1H=在Rt△ABD中,BD= ∴BG= ∴ (0≤x<2) 9. (2011广东株洲,20,6分)如图, △ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC. (1)求∠ECD的度数; (2)若CE=5,求BC长. 【答案】(1)解法一:∵DE垂直平分AC,∴CE=AE,∠ECD=∠A=36°. 中.考.资.源.网 解法二:∵DE垂直平分AC,∴AD=CD,∠ADE=∠CDE=90°, 又∵DE =DE,∴△ADE≌△CDE,∠ECD=∠A=36°. (2)解法一:∵AB=AC,∠A=36°,∴∠B=∠ACB=72°, ∵∠ECD=36°, ∴∠BCE=∠ACB-∠ECD=36°, ∠BEC=72°=∠B,中.考.资.源.网 ∴ BC=EC=5. 解法二:∵AB=AC,∠A=36°, ∴∠B=∠ACB=72°, ∴∠BEC=∠A+∠ECD=72°, ∴∠BEC=∠B, ∴BC=EC=5. 10.(2011重庆綦江,24,10分)如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE. (1) 求证:△ACD≌△BCE; (2) 延长BE至Q, P为BQ上一点,连结CP、CQ使CP=CQ=5, 若BC=8时,求PQ的长.中.考.资.源.网 【答案】:(1)证明ABC和△CDE均为等边三角形, ∴AC=BC , CD=CE 且∠ACB=∠DCE=60° ∵∠ACD+∠DCB=∠DCB+∠BCE=60° ∴∠ACD=∠BCE ∴△ACD≌△BCE (2)解:作CH⊥BQ交BQ于H, 则PQ=2HQ 在Rt△BHC中 ,由已知和(1)得∠CBH=∠CAO=30°,∴ CH=4 在Rt△CHQ中,HQ= ∴PQ=2HQ=6 11. (2011江苏扬州,23,10分)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC, (1)求证:△ABC是等腰三角形; (2)判断点O是否在∠BAC的角平分线上,并说明理由。中.考.资.源.网 【答案】(1)证明:∵OB=OC ∴∠OBC=∠OCB ∵BD、CE是两条高 ∴∠BDC=∠CEB=90° 又∵BC=CB ∴△BDC≌△CEB(AAS) ∴∠DBC=∠ECB ∴AB=AC ∴△ABC是等腰三角形。 (2)点O是在∠BAC的角平分线上。连结AO. ∵ △BDC≌△CEB ∴DC=EB, ∵OB=OC ∴ OD=OE 又∵∠BDC=∠CEB=90° AO=AO ∴△ADO≌△AEO(HL) ∴∠DAO=∠EAO ∴点O是在∠BAC的角平分线上。 12. (2011广东省,21,9分)如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止.不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2). (1)问:始终与△AGC相似的三角形有 及 ; (2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由); (3)问:当x为何值时,△AGH是等腰三角形? 【解】(1)△HGA及△HAB; (2)由(1)可知△AGC∽△HAB ∴,即,中.考.资.源.网 所以, (3)当CG<时,∠GAC=∠H<∠HAC,∴AC<CH ∵AG<AC,∴AG<GH 又AH>AG,AH>GH 此时,△AGH不可能是等腰三角形; 当CG=时,G为BC的中点,H与C重合,△AGH是等腰三角形; 此时,GC=,即x= 当CG>时,由(1)可知△AGC∽△HGA 所以,若△AGH必是等腰三角形,只可能存在AG=AH 若AG=AH,则AC=CG,此时x=9 综上,当x=9或时,△AGH是等腰三角形. 13. (2011湖北黄冈,18,7分)如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长. 第18题图 B A E D F C 【答案】连结BD,证△BED≌△CFD和△AED≌△BFD,求得EF=5 14. (2011湖北襄阳,21,6分) 如图6,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②③;①③②;②③①. (1)以上三个命题是真命题的为(直接作答) ; (2)请选择一个真命题进行证明(先写出所选命题,然后证明). 图6 【答案】(1)①②③;①③②;②③①. 3分 (2)(略) 6分 15. (2011山东泰安,29 ,10分)已知:在△ABC中,AC=BC,∠ACB=900,点D是AB的中点,点E是AB边上一点。 (1)直线BF垂直于CE于点F,交CD于点G(如图①),求证:AE=CG; (2)直线AH垂直于CE于,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并说明。 【答案】(1)证明:∵点D是AB中点,AC=BC,∠ACB=900 ∴CD⊥AB,∠ACD=∠BCD=450 ∠CAD=∠CBD=450 ∴∠CAE=∠BCG 又BF⊥CE ∴∠CBG+∠BCG=900 又∠ACE+∠BCF=900 ∴∠ACE=∠CBG ∴△AEC≌△CGB ∴AE=CG (2)BE=CM 证明:∵CH⊥HM,CD⊥ED ∴∠CMA+∠MCH=900 ∠BEC+∠MCH=900 ∴∠CMA=∠BEC 又,AC=BC,∠ACM=∠CBE=450 ∴△BCE≌△CAM ∴BE=CM 16. 17. 18. 2011中考模拟分类汇编:等腰三角形 一、 选择题 1、(2011浙江杭州模拟16)下列命题正确的有 ( )个 ①400角为内角的两个等腰三角形必相似 ②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为750 ③一组对边平行,另一组对边相等的四边形是平行四边形 ④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2∶b2∶c2=2∶1∶1 ⑤若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形。 A、1个 B、2个 C、3个 D、4个 答案:A 2、(11年青岛二中)如图,等边的边长为3,为上一点,且,为上一点,若,则的长为( ) A. B. C. D. 答案:B 3、(2011杭州模拟)如图,在△ABC中,AC=BC,CD是AB边上的高线,且有2CD=3AB,又E,F为CD的三等分点,则∠ACB和∠AEB之和为: ……………… ( ▲ ) A.45° B.90° C. 60° D.75° 答案:B 4.(浙江省杭州市党山镇中2011年中考数学模拟试卷)若等腰三角形中有一个角等于,则这个等腰三角形的顶角的度数为( ) A. B. C.或 D.或中.考.资.源.网 答案:D B组 1. (2011深圳市全真中考模拟一)等腰三角形一腰上的高与另一腰的夹角为30。,则顶角的度数为 (A)60. (B)120. (C)60或150. (D)60或120 答案:D 2.(浙江杭州进化2011一模)如图,△ABC内接于⊙O,其外角平分线AD交⊙O于DM⊥AC于M,下列结论:①DB=DC;②AC-AB=2AM;③AC+AB=2CM;④=2其中正确的有( ) A.只有④② B.只有①②③ C.只有③④ D.①②③④ 答案: B中.考.资.源.网 A B C D E 3、(2011年杭州模拟17)如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为(2010沈阳中考第8题改编) A. 81 B . 81/2 C. 81/4 D. 81/8 答案:C 一、 填空题 A D C P B (第1题图) 60° 1、(2011年北京四中四模)如图,以A、B两点为其中两个顶点作位置不同的等边三角形,最多可以作出_____个. 答案:2 2、(2011北京四中模拟6)用两块完全重合的等腰三角形纸片能拼出下列图形中.考.资.源.网 . 答案 平行四边形,正方形,等腰直角三角形; 3、(2011浙江杭州模拟15)如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连结CD.若AB=4cm. 则△BCD的面积为 . 答案: P C B A 4、(2011浙江杭州模拟15)如图△ABC中,∠ACB=90°,BC=6 cm,AC=8cm,动点P从A出发,以2 cm / s的速度沿AB移动到B,则点P出发 s时,△BCP为等腰三角形. 答案: 2,2.5,1.4 5. (2011年江苏盐城)已知△ABC中,AB=AC,∠B=70°,则∠C的大小为 . 答案70° 6、(2011年浙江省杭州市模拟)等腰两边的长分别是一元二次方程的两个解,则这个等腰三角形的周长是 . 答案:7,9 B组 1. (2011深圳市中考模拟五)等腰三角形的腰长为2,腰上的高为1,则它的底角等于 . 答案: 15°或75° 2.( 2011年杭州三月月考)若一边长为40㎝的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过,则铁圈直径的最小值为 ▲ ㎝.(铁丝粗细忽略不计) 答案: 3、(北京四中2011中考模拟13)用两块完全重合的等腰三角形纸片能拼出下列图形 . 答案:平行四边形,正方形,等腰直角三角形; A D F C B E (第4题)图) 4.(2011年海宁市盐官片一模)如图,有一块边长为4的正方形塑料摸板,将一块足够大的直角三角板的直角顶点落在点,两条直角边分别与交于点,与延长线交于点.则四边形的面积是 . 答案:16 A B C D E O 第5题 5. (2011年浙江省杭州市模2) 如图,在半圆O中,直径AE=10,四边形ABCD是平行四边形,且顶点A、B、C在半圆上,点D在直径AE上,连接CE,若AD=8,则CE长为 . 答案: 一、 解答题 A组 1、(北京四中模拟7)已知:如图,在DABC中,ÐC=90°,AB的垂直平分线交AC于D,垂足为E.若ÐA=30°,DE=2,求ÐDBC的度数和CD的长. 答案 2 2、(2011浙江杭州模拟15) 如图(1)矩形纸片ABCD,把它沿对角线折叠,会得到怎么样的图形呢? B F C A D E 第2题图 G (1)在图(2)中用实线画出折叠后得到的图形(要求尺规作图,保留作图轨迹,只需画出其中一种情况) A D C B (2) (2)折叠后重合部分是什么图形?试说明理由。 A D C B (1) 答案: (1)图略 (4分) (2)等腰三角形 (1分) (2分) 3.(2011年重庆江津区七校联考)已知a、b、c分别是△ABC的三边,其中a=1,c=4,且关于x的方程有两个相等的实数根,试判断△ABC的形状. 答案: ∵关于x的方程有两个相等的实数根 ∴ △= ∴ ∴ △ABC是等腰三角形. 等腰三角形 一、选择题 1.(2010年黑龙江一模)如图,在等腰△ABC中,∠ ABC=1200, 点P是底边AC上一个动点, M、N分别是AB、BC 的中点, 若PM+PN的最小值为2,则△ABC的周长是( ) A.2 B. C. D. 答案:D 2.(2010年广州市中考七模)、已知等腰三角形的一个内角是30°,那么这个等腰三角形顶角的度数是( ) A.75° B. 120° C.30° D.30°或120°[中.考.资.源.网] 答案:D 3.(2010北京市朝阳区模拟)某等腰三角形的两条边长分别为3cm和6cm,则它的周长 为( ) A.9cm B.12cm C.15cm D.12cm或15cm 答案:C 4.(2010年河南中考模拟题6)一张折叠型方桌如图甲,其主视图如图乙,已知AO=BO=50cm,C0=D0=30 cm,现将桌子放平,要使桌面a距离地面m为40cm高,则两条桌腿需要叉开的角度∠AOB为( ) A.1200 B.1500 C.600 D.900 甲 答案:A 二、填空题 1.(2010年江西省统一考试样卷)如图,将一张等腰直角三角形纸片沿中位线剪开,若拼成下列四边形:①平行四边形;②梯形;③矩形;④菱形;⑤正方形,则可以拼成的四边形序号是 . 答案:①②③. 2、(2010年河南中考模拟题3) 如图,有一底角为35°的等腰三角形纸片,现过底边上一点,沿与底边垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中,最大角的度数是 。 答案:1250 三、解答题 1.(2010年广州中考数学模拟试题(四))如图,Rt△ABC中,∠C=90°,AC=4,BC=3,以△ABC的一边为边画等腰三角形,使它的第三个顶点在△ABC的其它边上.请在图①、图②、图③中分别画出一个符合条件的等腰三角形,且三个图形中的等腰三角形各不相同,并在图下方的横线上写明所画等腰三角形的腰和腰长(不要求尺规作图). A B C A B C A B C A B C BD=CD=2.5 AD=CD=2.5 AC=AD=4 AD=BD=25/8 D D D D A B C (第1题图) 图① 图② 图③ A B C A B C A B C D BC=BD=3 答案: A B C BC=CD=3 D 画图并且指明腰的每个1分,写出腰长的每个1分,只画图的不给分. 单元测试(满分100分) 一、基础过关训练 1.如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN等于( ) A. B. C. D. (第1题) (第2题) (第3题) 2.如图,有一底角为35°的等腰三角形纸片,现过底边上一点,沿与底边垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中,最大角的度数是______. 3.如图,将边长为1的正三角形OAP沿x轴正方向连续翻2008次,点P依次落在点P1,P2,P3,…,P2008的位置,则点P2008的横坐标为_______. 4.如图,△ABC为等腰三角形,把它沿底边BC翻折后,得到△DBC,请你判断四边形ABDC的形状,并说出你的理由. 二、能力提升训练 5.将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表: 所剪次数 1 2 3 4 … n 正三角形个数 4 7 10 13 … an 则an=_____________________________(用含n的代数式表示). (第5题) (第6题) 6.如图,C为线段AE上一动点(不与点A,E重合), 在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中恒成立的有______(把你认为正确的序号都填上). 7.文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”“求证”(如图),他们对各自所作的辅助线描述如下:[来源:Www.zk5u.com] 文文:“过点A作BC的中垂线AD,垂足为D”; 彬彬:“作△ABC的角平分线AD”. 数学老师看了两位同学的辅助线后,说:“彬彬的作法是正确的,而文文的作法需要证正”. (1)请你简要说明文文的辅助线作法错在哪里; (2)根据彬彬的辅助线作法,完成证明过程. 8.如图,已知AB=AC. (1)若CE=BD,求证:GE=GD; (2)若CE=mBD(m为正数),试猜想GE与GD有何关系.( 只写结论,不证明) 9.如图,E,F分别是等腰△ABC的腰AB,AC的中点. (1)用尺规在BC边上求作一点M,使四边形AEMF为菱形;(不写作法,保留作图痕迹); (2)若AB=5cm,BC=8cm,求菱形AEMF的面积. 10.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F, 点E是AB的中点,连结EF. (1)求证:EF∥BC;(2)若四边形BDFE的面积为6,求△ABD的面积. 11.在平面直角坐标系中: (1)若A点坐标为(1,1),在坐标轴上找一点P,使△POA为等腰三角形,这样的P点有多少个? (2)若A点坐标为(2,1),在y轴上找一点,使△POA为等腰三角形,这样的P点有多少个? (3)若A点坐标为(2,1),在坐标轴上是否存在P点,使△POA为等腰三角形?若存在,请写出符合条件的所有P点的坐标;若不存在,请说明理由.[来源:中.考.资.源.网] 参考答案 基础过关训练 1.C 2.125° 3.2008 4.解:ABDC是菱形. ∵△ABC是等腰三角形,∴AB=AC. 又△ABC≌△DBC,∴BD=AB,DC=AC, ∴AB=BD=DC=AC,∴四边形ABDC是菱形. 能力提升训练 5.3n+1 6.①②③⑤ 7.(1)BC的中垂线不一定经过A点 (2)略 8.(1)证明:方法一,如图1,过D点作DM∥AE交BC于点M. ∴∠1=∠ACB,∠3=∠2. ∵AB=AC,∴∠B=∠ACB. ∴∠B=∠1,∴BD=DM. 又∵CE=BD,∴CE=DM. 在△DMG和△ECG中, ∴△DMG≌△ECG(AAS). ∴GE=GD. 图1 图2 方法二,如图2,过点E作EN∥AB交BC的延长线于点N. ∴∠B=∠B. 又AB=AC,∴∠B=∠1,∠1=∠2.[来源:中.考.资.源.网] ∴∠B=∠2=∠N,∴CE=NE. 又∵BD=CE,∴NE=BD. 在△BDG和△NEG中, ∴△BDG≌△NEG,∴DG=GE. (2)GE与GD的关系是:GE=mGD. 9.解:(1)如图. (2)由(1)知:M是BC的中点. ∵AB=AC,∴AM⊥BC. ∵AB=5cm,BC=8cm, ∴EF=4cm,BM=4cm. AM==3. ∴S菱形AEMF=×3×4=6(cm2). 10.(1)证明:∵DC=AC,CF平分∠ACB, ∴F是AD的中点. 又∵E是AB的中点,∴EF∥BC. (2)解:设△ABD的面积为S. 由(1)知EF=BD,△AEF∽△ABD. ∴=()2,∴S=8. ∴△ABD的面积为8. 11.解:(1)8个.(2)4个.(3)存在.有8个.它们是中.考.资.源.网 P1(,0),P2(-,0),P3(4,0),P4(0,2),P5(0,), P6(0,-),P7(0,),P(,0)查看更多