2020九年级数学上册 第23章 旋转章末复习导学案 （新版）新人教版

2020九年级数学上册 第23章 旋转章末复习导学案 （新版）新人教版

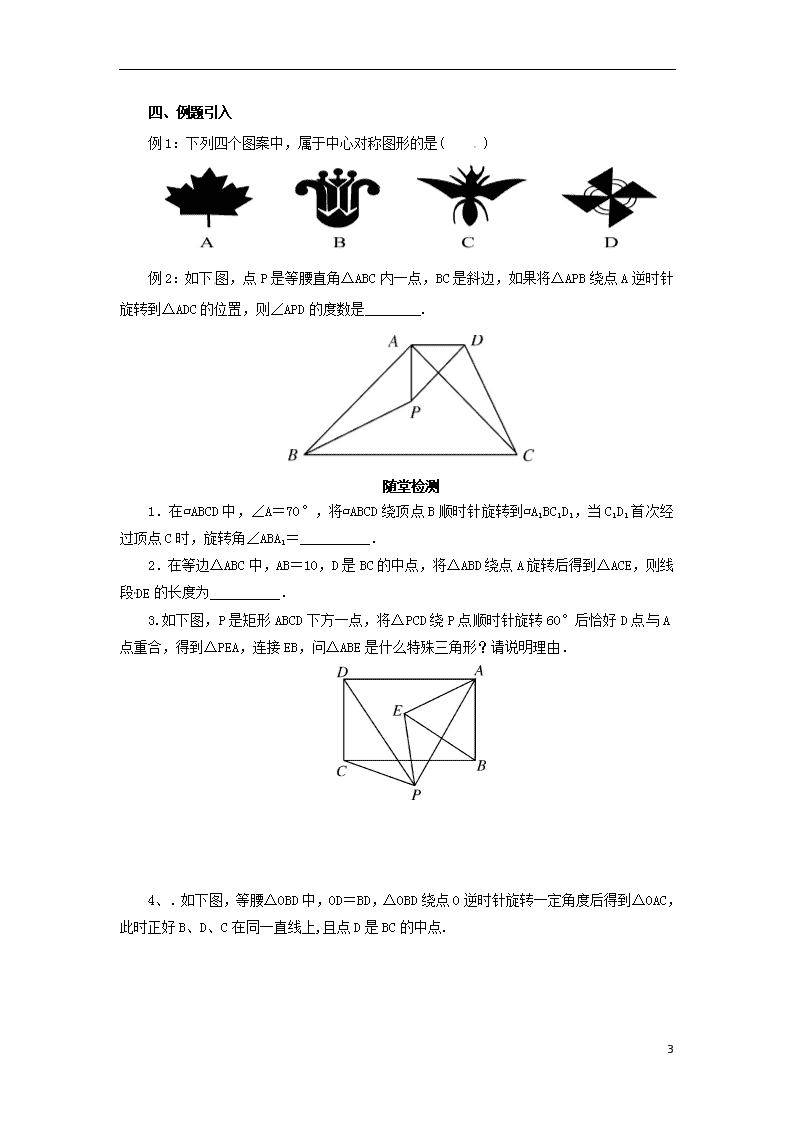
‎23 章末复习 一、知识框架 二、要点梳理 ‎1．把一个图形绕着某一个点O转动一定角度的图形变换叫做______________，如果图形上的点P经过旋转变为点P′，那么这两个点叫做这个旋转的对应点．‎ ‎2．旋转变换的性质 ‎(1)对应点到旋转中心的距离 ___________ ；‎ ‎(2)对应点与旋转中心所连线段的夹角等于 ___________；‎ ‎(3)旋转前、后的图形全等．‎ ‎3．把一个图形绕着某一个点旋转 ___________ ，如果它能够与另一个图形重合，那么就说这两个图形关于这个点成中心对称，这个点叫做 ___________，这两个图形中的对应点叫做关于中心的对称点．‎ 6‎ 关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心平分．关于中心对称的两个图形是 ___________‎ ‎4．把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做___________ ，这个点就是它的___________ ‎ ‎5．确定一个旋转运动的条件是要确定___________ ‎ 三、方法指导 ‎1、中心对称与中心对称图形 中心对称与中心对称图形的区别：中心对称是两个图形的位置关系，必须涉及两个图形，中心对称图形是指一个图形；中心对称是指其中一个图形沿对称中心旋转180°后，两个图形重合；中心对称图形是指该图形绕对称中心旋转180°，与原图形重合．‎ 中心对称与中心对称图形的联系：如果把两个成中心对称的图形拼在一起，看成一个整体，那么它就是中心对称图形；如果把中心对称图形看成以对称中心为分点的两个图形，那么这两个图形成中心对称 ‎2、中心对称与轴对称 中心对称与轴对称的区别：中心对称有一个对称中心——点；图形绕中心旋转180°，旋转后与另一个图形重合．轴对称有一条对称轴——直线．图形沿直线翻折180°，翻折后与另一个图形重合．‎ 中心对称与轴对称的联系：如果一个轴对称图形有两条互相垂直的对称轴，那么它必是中心对称图形，这两条对称轴的交点就是它的对称中心，但中心对称图形不一定是轴对称图形．‎ ‎3、方法技巧 图形的旋转方向可以是顺时针也可以是逆时针，经过旋转，图形的位置可能发生改变，也可能不发生改变．(当图形旋转360°时，图形的位置没有改变)‎ ‎4、旋转作图 ‎(1)旋转作图的依据是旋转的特征．‎ ‎(2)旋转作图的步骤如下：‎ ‎①确定旋转中心、旋转方向和旋转角度；‎ ‎②确定图形的关键点(如三角形的三个顶点)，并标上相应字母；‎ ‎③将这些关键点沿旋转方向转动一定的角度；‎ ‎④按照原图形的连接方式，顺次连接这些对应点，得到旋转后的图形，写出结论．‎ 6‎ 四、 例题引入 例1：下列四个图案中，属于中心对称图形的是( )‎ 例2：如下图，点P是等腰直角△ABC内一点，BC是斜边，如果将△APB绕点A逆时针旋转到△ADC的位置，则∠APD的度数是________.‎ 随堂检测 ‎1．在▱ABCD中，∠A＝70°，将▱ABCD绕顶点B顺时针旋转到▱A1BC1D1，当C1D1首次经过顶点C时，旋转角∠ABA1＝__________．‎ ‎2．在等边△ABC中，AB＝10，D是BC的中点，将△ABD绕点A旋转后得到△ACE，则线段DE的长度为__________．‎ ‎3.如下图，P是矩形ABCD下方一点，将△PCD绕P点顺时针旋转60°后恰好D点与A点重合，得到△PEA，连接EB，问△ABE是什么特殊三角形？请说明理由．‎ ‎4、．如下图，等腰△OBD中，OD＝BD，△OBD绕点O逆时针旋转一定角度后得到△OAC，此时正好B、D、C在同一直线上,且点D是BC的中点.‎ 6‎ ‎5.如下图，将△ABC绕点B逆时针旋转α得到△DBE，DE的延长线与AC相交于点F，连接DA、BF， ∠ABC＝α＝60°，BF＝AF.(1)求证：DA∥BC；(2)猜想线段DF、AF的数量关系，并证明你的猜想．‎ 课堂小结 我的收获 ‎________________________________________________________________________________________________________________________________________________________‎ 6‎ 参考答案 要点梳理 1、 旋转；‎ 2、 相等；旋转角 3、 ‎1800；对称中心；全等图形 4、 中心对称图形；对称中心 5、 旋转中心、旋转方向和旋转角度 探究案 例题解析：‎ 例1：D 例2：45°‎ 随堂检测 ‎1、40°‎ ‎2、‎ ‎3、【解析】△ABE是等边三角形．‎ 由旋转性质得△PAE≌△PDC,所以PA＝PD，AE＝DC＝AB，再由∠DPA＝60°得△PAD是等边三角形，从而得∠PDC＝∠PAE＝∠PAB＝30°，所以∠EAB＝60°，得证．‎ ‎【答案】解：△ABE是等边三角形，理由如下：‎ ‎ 由旋转，得△PAE≌△PDC，∴CD＝AE，PD＝PA，∠PDC＝∠PAE，∵∠DPA＝60°，∴△PAD是等边三角形，∴∠PDA＝∠PAD＝60°，又CD＝AB，∠CDA＝∠DAB＝90°，∴∠PDC＝∠PAB＝∠PAE＝30°，∴AE＝CD＝AB，∠EAB＝∠PAB＋∠PAE＝60°，∴△ABE是等边三角形．‎ ‎4、（1）由旋转得△OAC≌△OBD，∴OC＝OD又CD＝BD＝OD，∴OC＝OD＝CD，∴△OCD是等边三角形，∴∠COD＝60°，∴旋转角为60°‎ ‎（2）∵△OAC≌△OBD，△OCD是等边三角形， ∴AC＝BD＝CD，∠OCA＝∠ODB＝180°－60°＝120°， ∴∠ACD＝∠OCA－∠OCD＝60° ∴△ACD是等边三角形，‎ ‎ ∴OD＝OC＝AC＝AD， ∴四边形ODAC是菱形．‎ ‎5、（1）由旋转得∠DBE＝∠ABC＝60°，BD＝AB， ∴△ABD是等边三角形，∴∠DAB＝60°，‎ 6‎ ‎ ∴∠DAB＝∠ABC，∴DA∥BC；‎ ‎（2）DF＝2AF，证明如下：在DF上截取DG＝AF， 连接BG，则△DBG≌△ABF，∴BG＝BF， ∠DBG＝∠ABF，∴∠GBF＝∠DBE＝60°， ∴△BGF是等边三角形，∴GF＝BF＝AF，‎ ‎ ∴DF＝DG＋FG＝2AF．‎ 6‎