江苏省扬州中学2017届高三下学期开学考试（2月）+数学试卷（含附加题及答案）

江苏省扬州中学2017届高三下学期开学考试（2月）+数学试卷（含附加题及答案）

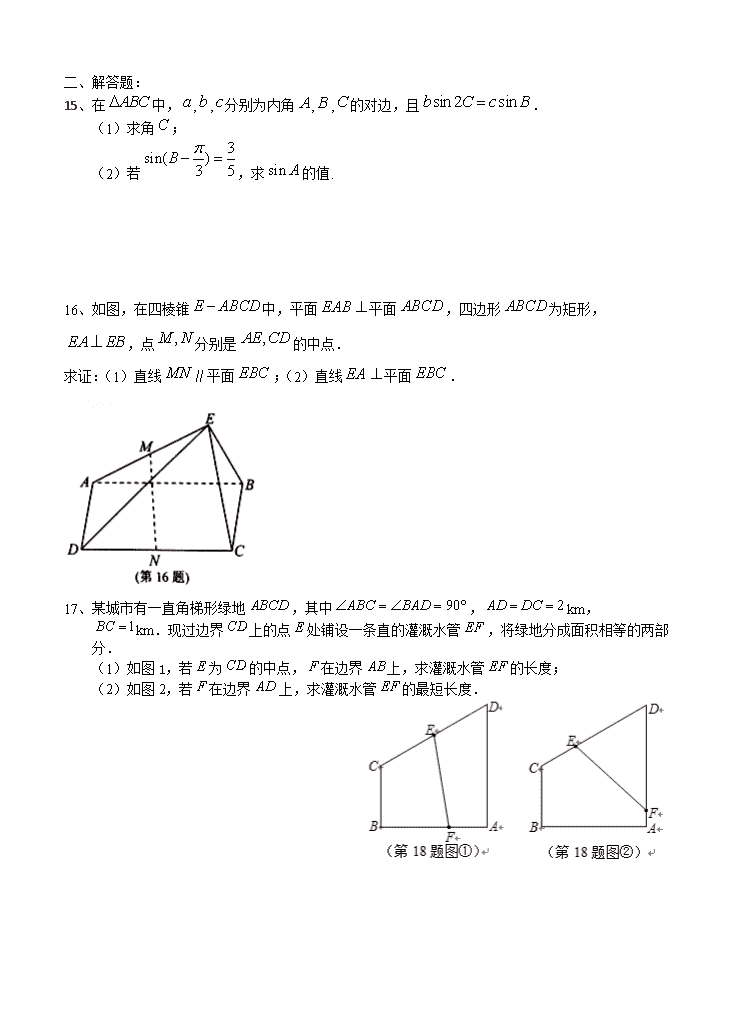
江苏省扬州中学高三下开学考试 一、 填空题：‎ ‎1、设集合，，，则 ▲ ．‎ ‎2、设复数满足，其中为虚数单位，则的虚部为 ▲ .‎ ‎3、设向量，，若，则实数 ▲ ．‎ ‎4、已知样本数据的方差，则样本数据的方差为 ▲ .‎ ‎5、已知函数是定义在R上的周期为2的奇函数，当时，，则 ▲ ．‎ ‎6、若圆锥底面半径为，高为，则其侧面积为 ▲ ．‎ ‎7、数列为等比数列，且成等差数列，则公差 ▲ ．‎ ‎8、如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北30°的方向上，行驶600 m后到达B处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD＝ ▲ m.‎ ‎9、如图，在平面直角坐标系中，已知，，分别为椭圆的右、下、上顶点，是椭圆的右焦点．若，则椭圆的离心率是 ▲ ‎ ‎10、已知函数f(x)＝sin2＋sin ωx－ (ω>0，x∈R).若f(x)在区间(π，2π)内没有零点，则ω的取值范围是 ▲ ．　‎ ‎11、若实数x，y满足2x2＋xy－y2＝1，则的最大值为 ▲ ．‎ ‎12、已知向量a，b，|a|＝1，|b|＝2.若对任意单位向量e，均有|a·e|＋|b·e|≤，则a·b的最大值是 ▲ ．‎ ‎13、已知函数，若关于的方程恰有三个不同的实数解，则满足条件的所有实数的取值集合为 ▲ ．‎ ‎14、已知函数与函数的图象共有（）个公共点：，‎ ‎，… ，，则 ▲ ． ‎ 一、 解答题：‎ ‎15、在中，,,分别为内角,,的对边，且．‎ ‎（1）求角；‎ ‎（2）若，求的值.‎ ‎16、如图，在四棱锥中，平面平面，四边形为矩形，‎ ‎，点分别是的中点．‎ 求证：（1）直线∥平面；（2）直线平面．‎ ‎17、某城市有一直角梯形绿地，其中，km，km．现过边界上的点处铺设一条直的灌溉水管，将绿地分成面积相等的两部分．‎ ‎（1）如图1，若为的中点，在边界上，求灌溉水管的长度；‎ ‎（2）如图2，若在边界上，求灌溉水管的最短长度．‎ ‎18、如图所示，椭圆C：，左右焦点分别记作、，过、分别作直线、交椭圆于、，且⫽．‎ ‎（1）当直线的斜率与直线的斜率都存在时，求证：为定值；‎ ‎（2）求四边形面积的最大值．‎ ‎19、已知函数f（x）=x2﹣（a+2）x+alnx，其中常数a＞0．‎ ‎（Ⅰ）当a＞2时，求函数f（x）的单调递增区间；‎ ‎（Ⅱ）设定义在D上的函数y=h（x）在点P（x0，h（x0））处的切线方程为l：y=g（x），若＞0在D内恒成立，则称P为函数y=h（x）的“类对称点”．当a=4时，试问y=f（x）是否存在“类对称点”，若存在，请至少求出一个“类对称点”的横坐标；若不存在，请说明理由．‎ ‎20、已知无穷数列的各项都是正数，其前项和为，且满足：，，其中，常数．‎ ‎（1）求证：是一个定值；‎ ‎（2）若数列是一个周期数列（存在正整数，使得对任意，都有成立，则称为周期数列，为它的一个周期），求该数列的最小周期；‎ ‎（3）若数列是各项均为有理数的等差数列，（），问：数列 中的所有项是否都是数列中的项？若是，请说明理由；若不是，请举出反例．‎ ‎ 江苏省扬州中学高三下开学考试附加题 ‎21、已知矩阵A＝属于特征值l的一个特征向量为α＝ ．‎ ‎（1）求实数b，l的值；‎ ‎（2）若曲线C在矩阵A对应的变换作用下，得到的曲线为C¢：x2＋2y2＝2，求曲线C的方程．‎ ‎22、在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线的极坐标方程为． ‎ ‎（Ⅰ）把曲线的参数方程化为极坐标方程；‎ ‎（Ⅱ）曲线与曲线交于点、，曲线与曲线交于点、，求．‎ ‎23、如图，在四棱锥中，平面，， ，，为的中点．‎ ‎（1）求异面直线，所成角的余弦值；‎ ‎（2）点在线段上，且，若直线与平面所成角的正弦值为，求的值．‎ ‎24、已知展开式的各项依次记为．‎ 设．‎ ‎（1）若的系数依次成等差数列，求的值；‎ ‎（2）求证：对任意，恒有.‎ 5‎ 高三下开学考试答案 一、填空题：‎ 一、 ‎ 2、1 3、3　 4、12‎ ‎5、-2 6、 7、3 8、100 9、‎ ‎10、∪ 11、 12、1 ‎ ‎13、 14、3‎ 二、解答题：‎ ‎15、‎ 解：（1）由，根据正弦定理，得， …2分 因为，所以， …………4分 又，所以. …………6分 ‎（2）因为，所以，所以，‎ ‎ 又，所以. …………8分 又，即，‎ 所以 ‎ ‎ ‎. …………14分 ‎16、‎ ‎（1）取中点，连结，，‎ 又是的中点，所以，‎ 又是矩形边的中点，‎ 所以，所以，‎ 所以四边形是平行四边形，…4分 所以，‎ 又平面，平面，‎ 所以∥平面．……………………7分 ‎（2）在矩形中，，‎ 又平面平面，平面平面，平面，‎ 所以平面，……………………………10分 又平面，所以，‎ 又，，，平面，‎ 所以平面．………………14分 ‎17、（1）因为，，，‎ 所以，……………………………………2分 取中点，‎ 则四边形的面积为，‎ 即，‎ 解得，…………………………………………6分 所以(km)．‎ ‎ 故灌溉水管的长度为km．……………………8分 ‎（2）设，，在中，，‎ 所以在中，，‎ 所以，‎ 所以的面积为，‎ 又，所以，即．………12分 在中，由余弦定理，得，‎ 当且仅当时，取“”．‎ 故灌溉水管的最短长度为km．………16分 ‎18、证明：（1）设，，根据对称性，有 因为，都在椭圆C上，所以， ‎ 二式相减，‎ 所以为定值 ‎（2）（Ⅰ）当的倾角为时，与重合，舍 ‎（Ⅱ）当的倾角不为时，由对称性得四边形为平行四边形 ‎ 设直线的方程为 ‎ 代入，得 ‎ 显然，，‎ 所以 设，所以，，‎ 所以 ‎ 当且仅当即时等号成立。‎ 所以，‎ 所以平行四边形面积的最大值为，‎ ‎19、解：（Ⅰ）函数f（x）的定义域为（0，+∞），‎ ‎∵，‎ ‎∴‎ ‎∵a＞2，∴‎ 令f′（x）＞0，即 ‎∵x＞0，∴0＜x＜1或 所以函数f（x）的单调递增区间是（0，1），‎ ‎（Ⅱ）猜想y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为．‎ 下面加以证明：‎ 当时，…‎ ‎①当时，f（x）＜g（x）恒成立，‎ 等价于恒成立，‎ 令…‎ ‎∵，∴函数φ（x）在上单调递增，‎ 从而当时，恒成立，‎ 即当时，f（x）＜g（x）恒成立．‎ ‎②同理当时，f（x）＞g（x）恒成立．‎ 综上知y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为．‎ ‎20、解：（1）由 ①， 得 ②‎ ‎②－①，得， ‎ 因为，所以（定值）． ‎ ‎（2）当时，，故，， ‎ 根据（1）知，数列的奇数项和偶数项分别成等差数列，公差都是，所以，‎ ‎，， ‎ 当时，的奇数项与偶数项都是递增的，不可能是周期数列， ‎ 所以，所以，，所以，数列是周期数列，其最小周期为． ‎ ‎（3）因为数列是有理项等差数列，由，，，得 ‎，整理得，‎ 得（负根舍去），‎ 因为是有理数，所以是一个完全平方数，设（），‎ 当时，（舍去）． ‎ 当时，由，得，‎ 由于，，所以只有，符合要求，‎ 此时，数列的公差，所以（）．‎ 对任意，若是数列中的项，令，即，‎ 则，时，，时，，故不是数列中的项．‎ ‎21、解：（1）因为矩阵A＝属于特征值l的一个特征向量为α＝，‎ ‎ 所以＝l，即＝． ……………… 3分 从而解得b＝0，l＝2． ………… 5分 ‎（2）由（1）知，A＝．‎ 设曲线C上任一点M(x，y)在矩阵A对应的变换作用后变为曲线C¢上一点P(x0，y0)，‎ 则＝ ＝， ‎ 从而 ……………… 7分 因为点P在曲线C¢上，所以x02＋2y02＝2，即(2x)2＋2(x＋3y)2＝2，‎ 从而3x2＋6xy＋9y2＝1． ‎ 所以曲线C的方程为3x2＋6xy＋9y2＝1． ……………… 10分 ‎22、‎ 解 （Ⅰ）曲线的普通方程为，即，‎ 由，得，‎ 所以曲线的极坐标方程为 ．‎ ‎（Ⅱ）设点的极坐标为，点的极坐标为，‎ 则，，‎ 所以．‎ ‎23、（1）因为平面，且平面，‎ 所以，，‎ 又因为，所以两两互相垂直．‎ 分别以为轴建立空间直角坐标系，‎ 则由，可得 ‎，，，，，‎ 又因为为的中点，所以．‎ 所以，，…………2分 所以 ‎ ，‎ 所以异面直线，所成角的余弦值为．…………5分 ‎（2）因为，所以，则，‎ ‎，，‎ 设平面的法向量为，‎ 则 即 令，解得，，‎ 所以是平面的一个法向量．……………………………7分 因为直线与平面所成角的正弦值为，‎ 所以，‎ 解得，‎ 所以的值为．………………………………………………10分 ‎24、解：（1）依题意，，‎ 的系数依次为，，，‎ 所以，解得； ………4分 ‎（2）‎ 设，‎ 则 考虑到，将以上两式相加得：‎ 所以 又当时，恒成立，从而是上的单调递增函数，‎ 所以对任意，．‎ ‎ ………10分 欢迎访问“高中试卷网”——http://sj.fjjy.org 欢迎访问“高中试卷网”——http://sj.fjjy.org