- 2021-05-31 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修2同步练习:空间几何体 习题课
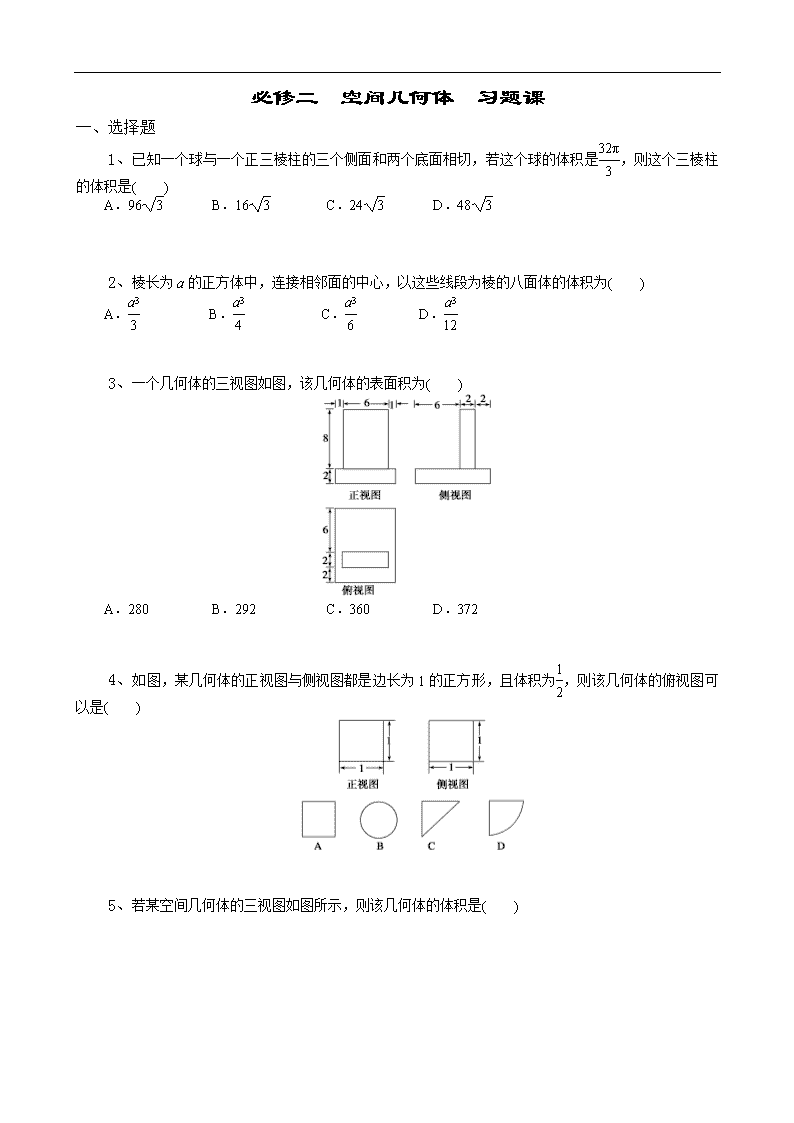
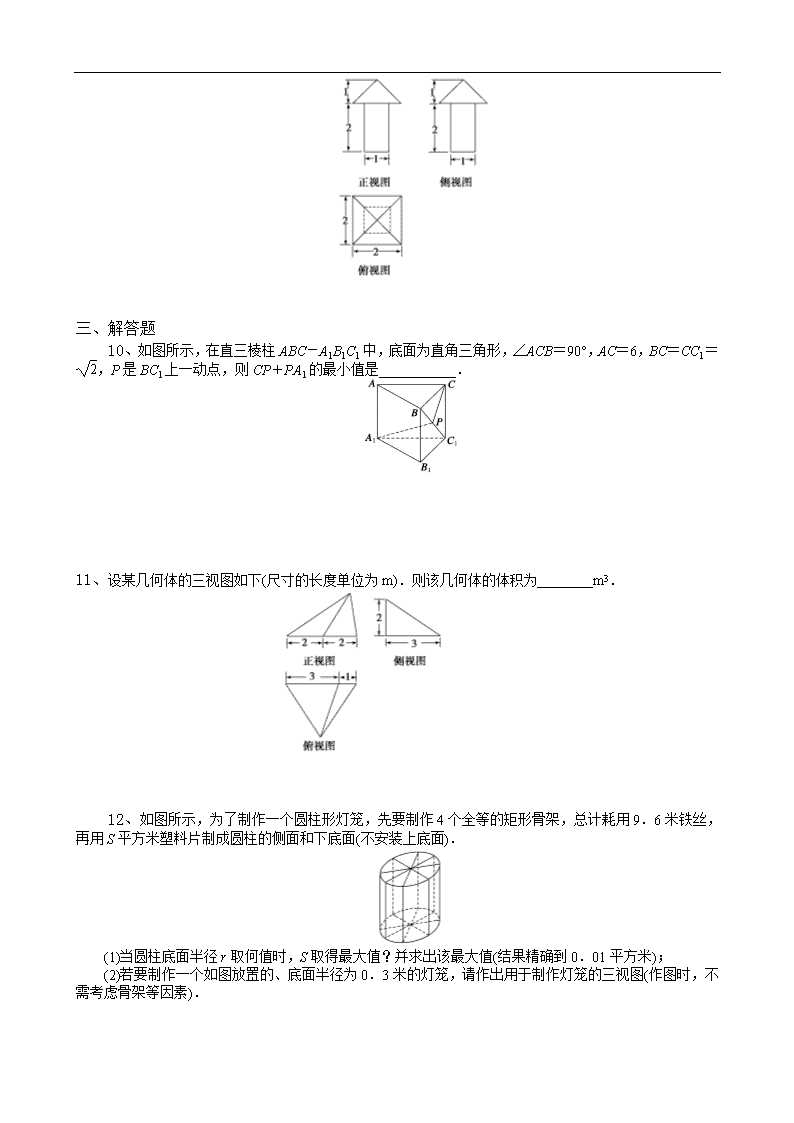
必修二 空间几何体 习题课 一、选择题 1、已知一个球与一个正三棱柱的三个侧面和两个底面相切,若这个球的体积是,则这个三棱柱的体积是( ) A.96 B.16 C.24 D.48 2、棱长为a的正方体中,连接相邻面的中心,以这些线段为棱的八面体的体积为( ) A. B. C. D. 3、一个几何体的三视图如图,该几何体的表面积为( ) A.280 B.292 C.360 D.372 4、如图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为,则该几何体的俯视图可以是( ) 5、若某空间几何体的三视图如图所示,则该几何体的体积是( ) A. B. C.1 D.2 6、圆柱的轴截面是正方形,面积是S,则它的侧面积是( ) A.S B.πS C.2πS D.4πS 二、填空题 7、圆柱形容器内盛有高度为8 cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm. 8、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是________cm3. 9、一个几何体的三视图如图所示,则这个几何体的体积为________. 三、解答题 10、如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1= ,P是BC1上一动点,则CP+PA1的最小值是___________. 11、设某几何体的三视图如下(尺寸的长度单位为m).则该几何体的体积为________m3. 12、如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面). (1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米); (2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出用于制作灯笼的三视图(作图时,不需考虑骨架等因素). 13、如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm). (1)按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积; 以下是答案 一、选择题 1、D [由πR3=,得R=2. ∴正三棱柱的高h=4. 设其底面边长为a, 则·a=2,∴a=4. ∴V=(4)2·4=48.] 2、C [连接正方体各面中心构成的八面体由两个棱长为a的正四棱锥组成,正四棱锥的高为,则八面体的体积为V=2××(a)2·=.] 3、C [由三视图可知该几何体是由下面一个长方体,上面一个长方体组合而成的几何体. ∵下面长方体的表面积为8×10×2+2×8×2+10×2×2=232,上面长方体的表面积为8×6×2+2×8×2+2×6×2=152,又∵长方体表面积重叠一部分,∴几何体的表面积为232+152-2×6×2=360.] 4、C [当俯视图为A中正方形时,几何体为边长为1的正方体,体积为1;当俯视图为B中圆时,几何体为底面半径为,高为1的圆柱,体积为;当俯视图为C中三角形时,几何体为三棱柱,且底面为直角边长为1的等腰直角三角形,高为1,体积为;当俯视图为D中扇形时,几何体为圆柱的,且体积为.] 5、C [由三视图可知,该空间几何体是底面为直角三角形的直三棱柱,三棱柱的底面直角三角形的直角边长分别为1和,三棱柱的高为,所以该几何体的体积V=×1××=1.] 6、B [设圆柱底面半径为r,则S=4r2, S侧=2πr·2r=4πr2=πS.] 二、填空题 7、4 解析 设球的半径为r cm,则πr2×8+πr3×3 =πr2×6r.解得r=4. 8、144 解析 此几何体为正四棱台与正四棱柱的组合体,而V正四棱台=(82+42+)×3=112,V正四棱柱=4×4×2=32,故V=112+32=144. 9、 解析 该几何体是上面是底面边长为2的正四棱锥,下面是底面边长为1、高为2的正四棱柱的组合体,其体积为 V=1×1×2+×22×1=. 三、解答题 10、5 解析 将△BCC1沿BC1线折到面A1C1B上,如图. 连接A1C即为CP+PA1的最小值,过点C作CD⊥C1D于D点,△BCC1为等腰直角三角形, ∴CD=1,C1D=1,A1D=A1C1+C1D=7. ∴A1C===5 . 11、4 解析 由三视图可知原几何体是一个三棱锥,且三棱锥的高为2,底面三角形的一边长为4,且该边上的高为3,故所求三棱锥的体积为V=××3×4×2=4 m3. 12、解 由题意可知矩形的高即圆柱的母线长为=1.2-2r,∴塑料片面积S=πr2+2πr(1.2-2r)=πr2+2.4πr-4πr2=-3πr2+2.4πr=-3π(r2-0.8r)=-3π(r-0.4)2+0.48π. ∴当r=0.4时,S有最大值0.48π,约为1.51平方米. (2)若灯笼底面半径为0.3米,则高为1.2-2×0.3=0.6(米).制作灯笼的三视图如图. 13、解 (1)如图所示. (2)所求多面体体积V=V长方体-V正三棱锥 =4×4×6-××2= (cm3).查看更多