2020届高三九师联盟11月联考数学试卷(理)
20 19�2020学年高三11月质扯检测
数学(理科)
考生注意:
1. 本试卷分选择题和非选择题两部分。满分150分,考试时间120分钟。
2. 答题前,考生务必用直径 o. 5毫米黑色墨水签字笔将密封线内项目填写
清楚。
3. 考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用2B铅
笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径 o. 5毫术黑色
墨水签字 笔在 答题卡上各题的答题区域内作 答, 超出答题区域书写的答
案无效,在试题卷、草稿纸上作答无效。 ..
4. 本卷命题范围:集合、常用逻辑用语、函数、导数及其应用、三角函数、三角恒等变换、解三角形、平
面向量、数列、不等式、立体几何。
一 、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1. 下列集合中不同千另外三个集合的是
A. { x飞 3 = 1}
2. 下列说法正确的是
B. {x [x 4= 1} C. { 1} n{xl±-1}
A若a>b, 则ac 4>bc、4 1 B. 若 a
-1
a b 2
C. 若a>b>c, 则a z>b2>产 D.若a>b,c>d, 则a+c>b+d
3. 巳知向量a = (x,3) , b = ( — 2 ,7), 若(a — b)_lb, 则实数x的值为
A. -16 B.-—6
7
6_7 c D.16
4. 若函数f (x ) = e工1 ' 则曲线 y = f ( x)在点( 1 1
—2 ,f( —
了))处 的切线方程为
A. 2x+y+2=0 B. 2x —y+2=0
5. 下列命题中正确的是
A. 若 三个平面两两相交,则它们的交线互相平行
B. 若 三条直线 两两相交, 则它们最多确定一个平面
C. 若不同的两条直线均垂直于同 一 个平面,则这两条直线平行
C. 2x+y —2=0 D. 缸 — y-2 = 0
D. 不 共线的四点可以确定一 个平面
6. 若关千x的不等式x 2+ax —b0的解集 是
A ( —=, 勹) U Cl , +=) B. (— f ,1 )
C. ( -= , - 1) U ( ½, +=) D. (—1 分)
【高三11月质釐检测·数学 理科 第1页(共4页)】
7。 函数F(J)=3sin(ω J+骨 )(ω )0)的 相邻两条对称轴之间的距离为号,则 将F(J)的 图象向右平移晋
个单位长度,所 得函数图象的一个对称中心是
A· (晋 90)
c。 r平 ,0)� /
8。 已知实数Ω,乙 满足3>0,|引 +乙 =1,
A。 2018 I;.2019
D。 r~÷ 90) 0 /
+2L罟2的 最小值为
C。 2020
B。 4 ,0/
k
π
`
l
`
伤+1
2019
]
C
E)。 2021
9∩ 爿
9。 在单调递减的等比数列(G72)中 ,已 知c3,Ω 5为 一元二次方程J2一 西J+7ˉ九=0的 两个根,则 其前刀项
和为
Q″ ~1
A±L一上
^^· 729
。刀+1~1
R.兰_上
^· 243
Q?2-1
r′ 里_土。·
3mˉ 1
Q冗 +1-1
D兰 — 上^· 3m
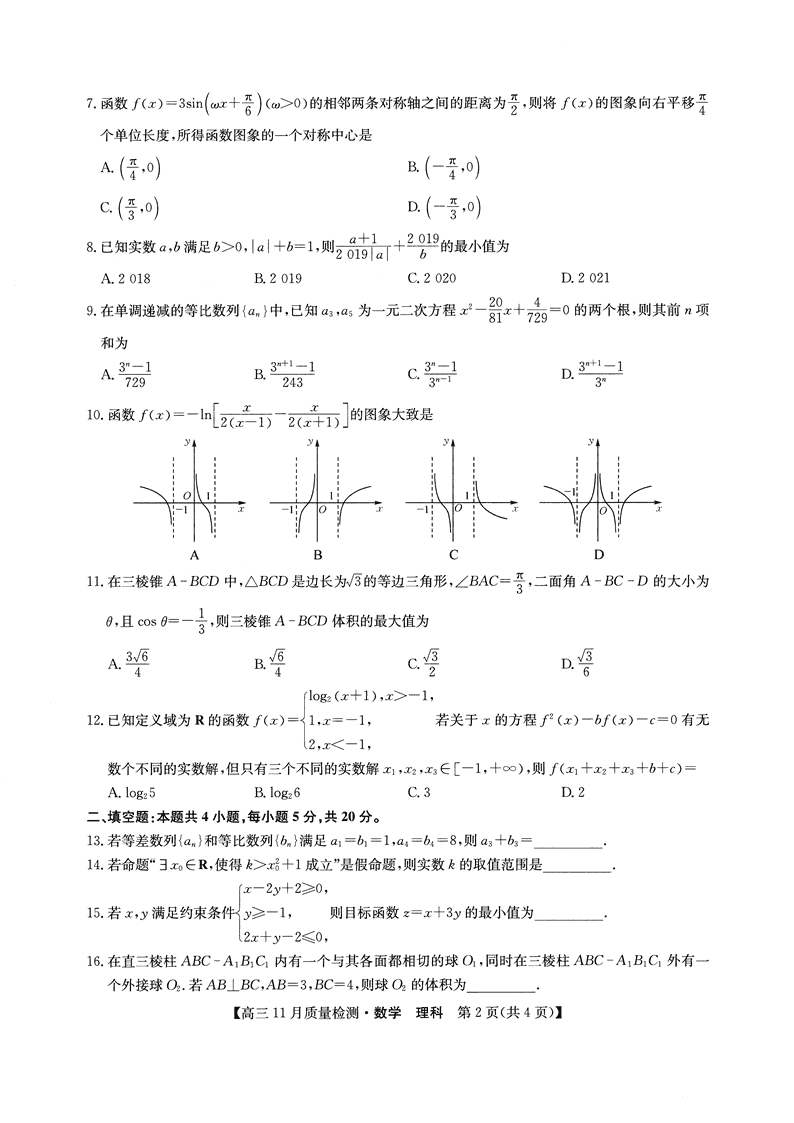
10。 函数F(J)=-ln J
2(J-1) 2(J+1)
J 的图象大致是Γ
L
γ
0
-1 @
A B C D
11。 在三棱锥A-BCD中 ,△ BCD是 边长为茯「的等边三角形,Z召AC=号 ,二 面角A-BC-D的 大小为
1
J,上三、cos汐 == ,则 三棱锥 A-BCD体积的最太值为3
一 6一
生
/V一
z
B一6一/√
一 准
3`一
12.已 知定义域为R的 函数r(J)
A。 C。
/t
丁`′√。
U。 ^丁
擂
一
2
log2(J+1),E>— 1,
1,J=-1, 若关于J的 方程F2(J)一 Dr(J)-c=o有无
2,r<-1,
数个不同的实数解,但只有三个不同的实数解J1,J2,J3∈ 匚一1,+∞ ),则 F(J1+J2+J3+3+c)=
A.log2 5 B。 log2 6 C。 3 D。 2
二、填空题:本题共4小题,每 小题5分 ,共 20分 。
13.若 等差数列(‰ )和等比数列(九 )满 足c1=31=1,G4=34=8,则 c3+33=
1⒋ 若命题“彐JO∈ R,使得尼>Jg+1成 立”是假命题,则 实数尼的取值范围早
15.若 J,y满 足约
J-2y+2∶≥0,
y≥ -1, 则目标函数z=J+3y的 最小值为
2J+丿 一2≤【0,
16.在 直三棱柱ABC-A1B1C1内 有一个与其各面都相切的球01,同 时在三棱柱ABC-A1B1Cl外 有一
个外接球02。 若AB⊥BC,AB=3,BC=4,则 球02的体积为
【高三11月 质量检测·数学 理科 第2页 (共 4页 )】
-1
三、解答题:共 70分 。解答应写出文字说明、证明过程或演算步骤。
17。 (本小题满分10分 )
已知在△ABC中 ,角 A,B,C的 对边分别为Ω,3,c,且 满足c2+32-c2=8,△ABC的 面积为2√
′了。
(1)求 角C的 大小;
(2)若 c=2√百,求 sin A+sin B的 值。
18。 (本 小题满分12分 )
城市中大量公园的兴建意味着建筑让位、还地于民,城 市公共空间被越来越充分地打开。这种打开不
只是物理意义上的空间开放,而是使城市公园不仅供民众用来休憩、娱乐、锻炼,还 用于相互交往、传
播文化、锤炼公民意识,让城市与人建立更好的连接,推动城市回归人本。某城市计划在靠近环城公路
AJ,Ay的 P处建一所职业技校,且配套修建一条道路BC,并把三条路围成的三角形区域开辟为休闲
公园(如 图)。 经测量P到 AJ,Ay的 距离PE,PF分 别为4 km,3 km,若 zBAC=卩 (卩 ∈(号 ,π )),
sin a=首 ,AB=J km,AC=y km。
(1)试 建立J,γ 间的等量关系;
(2)为 尽量减少土地占用,试 问如何确定B点 的位置,才 能使得该公园的面
积最小?并求最小面积。
(α +昔
)二
=<拜 ,0<α <∶ 晋,求 sin(α +号 )的值。
γ
A
P
E
19.(本小题满分12分 )
已知函数r(J)=4(sin ωJ-cos ωJ)Cos ωJ+2(ω)0)图 象的一个对称中心为(昔 ,0),设 函数r(J)
的最小正周期为T。
(1)求 T的 最大值;
(2)当 T取最大值时,若 F
【高三11月 质量检测·数学 理科 第3页 (共 4页 )】
20.(本小题满分12分 )
已知数列(‰ )的 前m项 和S叨 满足‰+1=2Sヵ 十6,且 a1=6.
(1)求 数列(‰ )的 通项公式;
(2)设数列召→的前m项 和为Tヵ 求证了
·手可
ˉ+了T瓦 +F:瓦 ^+ˉ +「-÷
瓦
(3
21.(本小题满分12分 )
如图,在 四棱锥S-ABCD中 ,底 面ABCD是 直角梯形,AD∥BC,AB⊥BC,△SAB是 等边三角形,侧
面SAB上 底面ABCD,AB=2茯 「,BC=3浊D=1,点 M是棱SB上靠近点S的一个三等分点。
(1)求证:AM∥平面SCD;
(2)求 二面角S-CD-B的 大小。
s
C
22.(本小题满分12分 )
已知函数只J)=2Jˉ1-(c+2)J,g(J)=-c(1+ln J)(c∈ R)。
(1)讨 论函数r(J)的 单调性;
(2)若 对任意的J∈ 匚1,+∞ ),F(J)≥ g(J)恒 成立,求 实数c的取值范围。
A D
【高三11月 质量检测·数学 理科 第4页 (共 4页 )】