2017-2018学年江苏省宿迁市沭阳县高二下学期期中考试数学试题 Word版

2017-2018学年江苏省宿迁市沭阳县高二下学期期中考试数学试题 Word版

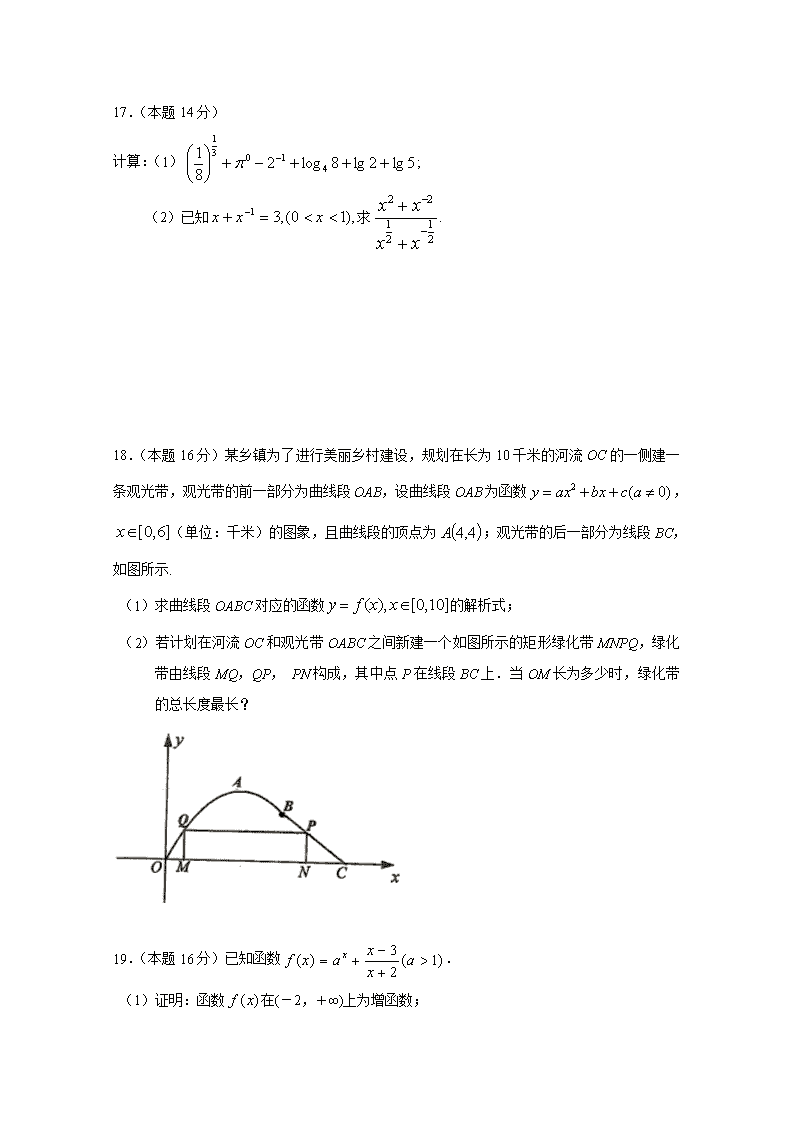
‎2017-2018学年江苏省宿迁市沭阳县高二下学期期中考试 数学试题 注意事项：‎ ‎1．本试卷共4页，包括填空题（第1题～第14题），解答题（第15题～第20题）两部分．试卷满分为160分，考试时间为120分钟．‎ ‎2．答题前，请务必将自己的姓名、 学校、 班级、 准考证号写在答题卡上并填涂准考证号．试题的答案写在答题卡相应题目的答题区域内．考试结束后，交回答题卡．‎ 一、填空题：本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请 将答案填写在答题卡相应的位置上． ‎ ‎1．设集合A={1，3}，集合B={1，2，4}，则集合A∪B= ▲ ．‎ ‎2．已知复数是实数，则实数 ▲ ．‎ ‎3．用反证法证明某命题时，对结论“自然数至少有1个奇数”的正确假设为“假设自然数 ▲ ”．‎ ‎4．若函数的值域为 , 则其定义域为 ▲ ．‎ ‎5．已知；；．则的大小关系是（从大到小排列）‎ ‎ ▲ ．‎ ‎6．已知复数对应的点在轴上方，则的取值范围是 ‎ ▲ ．‎ ‎7．若函数是偶函数，则的递增区间是 ▲ ．‎ ‎8．已知正三角形，它一边上的高为，内切圆的半径为，则，类比这一结论可知:正四面体的底面上的高为，内切球的半径为，则 ▲ . ‎ ‎9．已知函数在区间（）上存在零点，则 ▲ ．‎ ‎10．已知幂函数的图象过点，则的值为 ▲ .‎ ‎11．已知为偶函数，则 ▲ ． ‎ ‎12．已知函数，若，则 ▲ .‎ ‎13．已知且，则实数的取值范围是▲ ．‎ ‎14．设已知函数，正实数满足，且，若在区间上的最大值为2，则= ▲ ． ‎ 二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤．‎ ‎15．（本题14分）已知集合，，，全集为实数集．‎ ‎（1）求和；‎ ‎（2）如果，求的取值范围．‎ ‎16．（本题14分）已知复数满足（为虚数单位）．‎ ‎（1）求复数和；‎ ‎（2）求复数的模．‎ ‎17．（本题14分）‎ 计算：（1）;‎ ‎（2）已知求.‎ ‎18．（本题16分）某乡镇为了进行美丽乡村建设，规划在长为10千米的河流OC的一侧建一条观光带，观光带的前一部分为曲线段OAB，设曲线段OAB为函数，（单位：千米）的图象，且曲线段的顶点为；观光带的后一部分为线段BC，如图所示.‎ ‎（1）求曲线段OABC对应的函数的解析式；‎ ‎（2）若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ，绿化带由线段MQ，QP， PN构成，其中点P在线段BC上．当OM长为多少时，绿化带的总长度最长？‎ ‎19．（本题16分）已知函数． ‎ ‎（1）证明：函数在(－2，＋∞)上为增函数；‎ ‎（2）用反证法证明：方程没有负数根．‎ ‎20．（本题16分）已知函数，‎ ‎（1）若的解集为，求的值；‎ ‎（2）求函数在上的最小值；‎ ‎（3）对于，使成立，求实数的取值范围．‎ ‎2017～2018学年度第二学期期中调研测试 高二数学参考答案 一、填空题:本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请 将答案填写在答题卡相应的位置上． ‎ ‎1．设集合A={1，3}，集合B={1，2，4}，则集合A∪B=． ‎ ‎2．已知复数是实数，则实数 ．‎ ‎3．用反证法证明某命题时，对结论“自然数至少有1个奇数”的正确假设为“假设自然数都不是奇数”．‎ ‎4．若函数的值域为 , 则其定义域为．‎ ‎5．已知；；．则的大小关系是（从大到小排列）．‎ ‎6．已知复数对应的点在轴上方，则的取值范围是．‎ ‎7．若函数是偶函数，则的递增区间是．‎ ‎8．已知正三角形，它一边上的高为，内切圆的半径为，则，类比这一结论可知:正四面体的底面上的高为，内切球的半径为，则. ‎ ‎9．已知函数在区间（）上存在零点，则 3 ．‎ ‎10．已知幂函数的图象过点，则的值为 1 .‎ ‎11．已知为偶函数，则 4 ． ‎ ‎12．已知函数，若，则.‎ ‎13．已知且，则实数的取值范围 是．‎ ‎14．设已知函数，正实数满足，且，若在区间上的最大值为2，则=． ‎ 二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤．‎ ‎15．（本题14分）已知集合，，，全集为实数集．‎ ‎（1）求和；‎ ‎（2）如果，求的取值范围．‎ 解:（1）因为，，‎ 所以；……………………………………………………4分 所以． ……………………………………………8分 ‎（2）当时满足． ……………………………………………14分 ‎16．（本题14分）已知复数满足（为虚数单位）．‎ ‎（1）求复数和；‎ ‎（2）求复数的模．‎ 解：（1）； ……………………………………………3分 ‎； ……………………8分 ‎（2）， …………………12分 所以． …………………………………14分 ‎17．（本题14分）计算：（1）;‎ ‎（2）已知求.‎ 解：（1）原式= . ……………………………………7分 ‎（2）因为 …………………………9分 又因为，，所以 ‎ 所以. ………………………………………14分 ‎18．（本题16分）某乡镇为了进行美丽乡村建设，规划在长为10千米的河流OC的一侧建一条观光带，观光带的前一部分为曲线段OAB，设曲线段OAB为函数，（单位：千米）的图象，且曲线段的顶点为；观光带的后一部分为线段BC，如图所示.‎ ‎（1）求曲线段OABC对应的函数的解析式；‎ ‎（2）若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ，绿化带由线段MQ，QP， PN构成，其中点P在线段BC上．当OM长为多少时，绿化带的总长度最长？‎ 解：因为曲线段OAB过点，且最高点为，‎ 得， ‎ 所以，当时， ……………………………………4分 因为最后一部分是线段BC，，当时，‎ 综上，. …………………………8分 ‎（2）设则，由 得 所以点 ……………………………10分 所以，绿化带的总长度 ‎ ……14分 当时，.所以，当OM长为1千米时，绿化带的总长度最长. ………16分 ‎19．（本题16分）已知函数． ‎ ‎（1）证明：函数在(－2，＋∞)上为增函数；‎ ‎（2）用反证法证明：方程没有负数根．‎ 解：（1）证法1：任取，不妨设，则，，所以 又因为，所以 于是，‎ 故函数在(－2，＋∞)上为增函数．……………………………………………8分 证法2： ，‎ 在上恒成立，即在上为增函数．‎ ‎（2）假设存在满足 则，因为，，所以，所以，解得，与假设矛盾．‎ 故方程没有负数根． ………………………………………………16分 ‎20．（本题16分）已知，‎ ‎（1）若的解集为，求的值；‎ ‎（2）求函数在上的最小值；‎ ‎（3）对于，使成立，求实数的取值范围．‎ 解：（1）由得；整理得，‎ 因为不等式的解集为， ‎ 所以方程的两根是，；‎ 由根与系数的关系得，即； ……………4分 ‎（2）的对称轴方程为，‎ ‎①当时，即在上是单调增函数，故；‎ ‎②当时，即，在上是单调减函数，在上是单调增函数，故；‎ ‎③当时，即在上是单调减函数，故；‎ 所以………………………………………10分 ‎（3）因为函数在区间上为增函数，在区间上为减函数 其中，，所以函数在上的最小值为 对于使成立在上的 最小值不大于在上的最小值，‎ 由（2）知 ‎①‎ 解得,所以；‎ ‎②当时,‎ 解得，所以；‎ ‎③当时， ‎ 解得，所以 ‎ 综上所述，的取值范围是. …………………………………16分