2018-2019学年山东省临沂市罗庄区高一下学期期末考试 数学

2018-2019学年山东省临沂市罗庄区高一下学期期末考试 数学

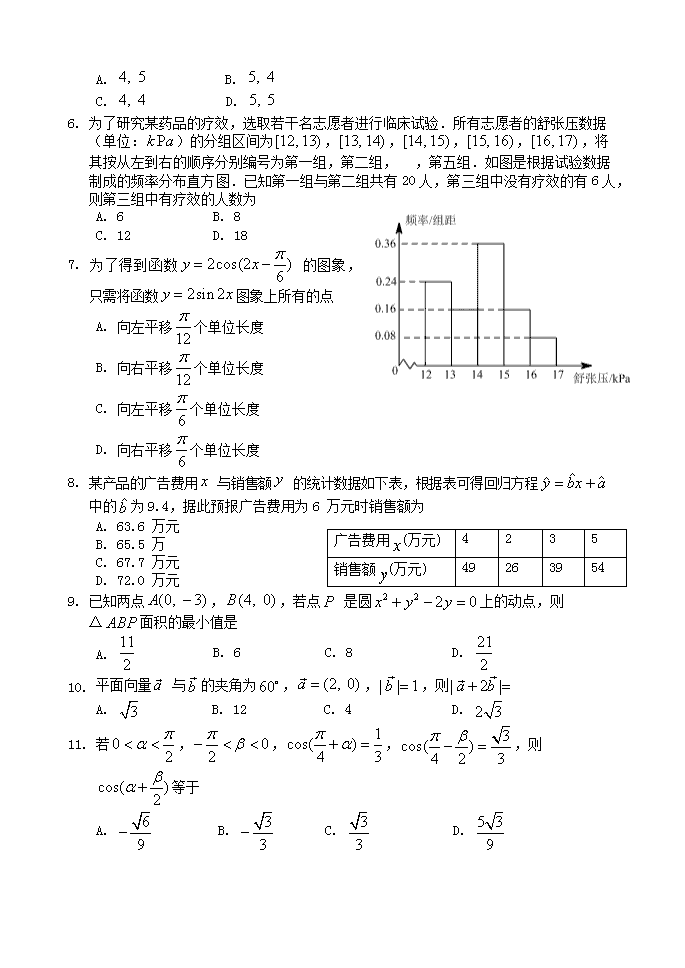
‎2018-2019学年山东省临沂市罗庄区高一下学期期末考试 ‎ 数 学 2019.07 ‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.‎ 注意事项：‎ 1. 答卷前，考生务必将自己的班级、姓名、准考证号、考试科目及试卷类型用中性笔和2B铅笔分别涂写在答题卡上；‎ 2. 将所有试题答案及解答过程一律填写在答题卡上.试题不交，只交答题卡.‎ 第I卷（选择题共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 某林场有树苗30000棵，其中松树苗4000棵．为调查树苗的生长情况，采用分层抽样的方法抽取一个容量为150 的样本，则样本中松树苗的数量应为 A. 30 B. 25 C. 20 D. 15‎ ‎2. 如果3个正整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数．从 中任取3个不同的数，则这3 个数构成一组勾股数的概率为 A. B. C. D. ‎ ‎3. 函数 的部分图象如图所示，则 的单调递减区间为 A. ‎ ‎ B. ‎ ‎ C. ‎ ‎ D. ‎ ‎4. 如图，正方形中， 是 的中点，若，则 A. B. C. D. ‎ ‎5. 茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩（单位：分）．已知甲组数据的众数为124，乙组数据的平均数即为甲组数据的中位数，则，的值分别为 ‎ A. B. ‎ C. D. ‎ ‎6. 为了研究某药品的疗效，选取若干名志愿者进行临床试验．所有志愿者的舒张压数据（单位：）的分组区间为，，，，，将其按从左到右的顺序分别编号为第一组，第二组，，第五组．如图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为 ‎ A. 6 B. 8 ‎ C. 12 D. 18‎ ‎7. 为了得到函数 的图象， ‎ 只需将函数图象上所有的点 ‎ A. 向左平移个单位长度 ‎ B. 向右平移个单位长度 C. 向左平移个单位长度 ‎ D. 向右平移个单位长度 ‎8. 某产品的广告费用 与销售额 的统计数据如下表，根据表可得回归方程 中的为9.4，据此预报广告费用为6 万元时销售额为 广告费用x(万元)‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y(万元)‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ A. 63.6 万元 ‎ B. 65.5 万 C. 67.7 万元 ‎ D. 72.0 万元 ‎9. 已知两点，，若点 是圆上的动点，则 ‎△面积的最小值是 ‎ A. ‎ B. 6 C. 8 D. ‎ 10. 平面向量 与的夹角为，，，则 A. B. 12 C. 4 D. ‎ ‎11. 若，，，，则等于 A. B. C. D. ‎ ‎12. 已知圆，直线，点在直线上，若存在圆上的点，使得（为坐标原点），则的取值范围是 ‎ A. B. C. D. ‎ 第II卷（非选择题共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分.把正确答案填在答题纸给定的横线上.‎ ‎13. 若是三角形的内角，且，则 等于 ．‎ ‎14. 过点作直线与圆 相交，则在弦长为整数的所有直线中，等可能的任取一条直线，则弦长长度不超过14的概率为______________.‎ ‎15. 矩形中，，，为矩形内部一点，且，若，则 的取值范围是 ．‎ ‎16. 已知圆，圆，，分别是圆， 上的动点，为轴上的动点，则 的最小值为 .‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程 ‎17. （本小题满分10分）‎ 在△ 中，内角，， 所对的边分别是，，，已知，，．‎ ‎（1）求；‎ ‎（2）求 的值．‎ ‎ ‎ ‎18.（本小题满分12分）‎ ‎ 已知向量，.‎ ‎（1）设，求 的单调递增区间；‎ ‎（2）若，向量 与 共线，且 为第二象限角，求 的值．‎ ‎ ‎ ‎19. 为了分析某名高一学生的学习状态，对其下一阶段的学习提供指导性建议．现对他前7 次考试的数学成绩 、物理成绩进行分析．下面是该生 7 次考试的成绩．‎ 数学 ‎108‎ ‎103‎ ‎137‎ ‎112‎ ‎128‎ ‎120‎ ‎132‎ 物理 ‎74‎ ‎71‎ ‎88‎ ‎76‎ ‎84‎ ‎81‎ ‎86‎ ‎（附：，）‎ ‎（1）他的数学成绩与物理成绩哪个更稳定?请给出你的说明；‎ ‎（2）已知该生的物理成绩与数学成绩 是线性相关的，求物理成绩与数学成绩 的回归直线方程；‎ ‎（3）若该生的物理成绩达到90 分，请你估计他的数学成绩大约是多少?‎ ‎ ‎ ‎20.（本小题满分12分）‎ ‎ 在△ 中，内角，， 所对的边分别是，，，，且 ‎．‎ ‎（1）求角 的大小；‎ ‎（2）若，，求△ 的面积．‎ ‎21.（本小题满分12分） ‎ 植树节期间我市组织义工参加植树活动，为方便安排任务将所有义工按年龄分组：第 1‎ 组 ，第 2 组，第 3 组，第 4 组，第 5 组 ‎，得到的部分频率分布表如下：‎ 区间 人数 频率 第1组 ‎[25,30)‎ ‎50‎ ‎0.1‎ 第2组 ‎[30,35)‎ ‎50‎ ‎0.1‎ 第3组 ‎[35,40)‎ ‎0.4‎ 第4组 ‎[40,45)‎ ‎150‎ ‎（1）求， 的值；‎ ‎（2）现在要从年龄较小的第 组中用分层抽样的方法随机抽取6 人担任联系人，在第 组抽取的义工的人数分别是多少?‎ ‎（3）在（2）的条件下，从这6人中随机抽取2人担任本次活动的宣传员，求至少有1 人年龄在第3 组的概率．‎ ‎ ‎ ‎22.（本小题满分12分）‎ 在平面直角坐标系 中，设圆 的圆心为．‎ ‎（1）求过点 且与圆 相切的直线的方程；‎ ‎（2）若过点且斜率为 的直线与圆相交于不同的两点，，以，为邻边作平行四边形，问是否存在常数，使得平行四边形 为矩形?请说明理由．‎ 高一质量调研试题 ‎ 数学试题参考答案 2019.07‎ 一、选择题： CADBA CCBAD DB 二、填空题：13. 或 14. 15. 16. ‎ 三、解答题：‎ ‎17. 解：（1） 因为，，，‎ 所以由余弦定理得：，‎ ‎ 则． ……………………………………………………………………5分 ‎      （2） 由正弦定理得，， …………6分 所以，， …………………8分 所以． …………………………………………10分 ‎18. 解：（1） ‎ ‎，………………………………………………………………3分 ‎ 由，得，………………5分 得 的单调递增区间为．…………………………6分 ‎      （2） 因为，， 与向量 共线，所以，即．………………………………………8分 又因为 是第二象限角，所以，………………………10分 ‎.…………………12分 ‎19. 解：（1），，……………………………………………………2分 所以数学的方差是， ………3分 物理的方差是， ……………4分 从而物理的方差小于数学的方差，‎ 所以物理成绩更稳定． ………………………………………………………………5分 ‎      （2） 由于 与 之间具有线性相关关系，‎ ‎，‎ ‎，……7分 所以，， …………………………………9分 所以线性回归方程为． ……………………………………………10分 ‎      （3） 当 时，由得，‎ 即该生物理是 分时，数学成绩大约是．………………………………………12分 ‎20.解： （1） 由题意，‎ 得，………………………2分 整理得，‎ 即．…………………………………………………4分 由，得．‎ 因为，所以，‎ 所以，‎ 所以．…………………………………………………………………………6分 ‎  （2） 因为在△ 中，，，，‎ 由正弦定理，得，解得．………………………………………7分 由，得．………………………………………………………………8分 所以．…………………………………………………9分 又因为 ‎ ‎，……………………………………………………10分 所以 .……………12分 ‎21. 解：（1） 根据题意知，，所以共有500 人参加活动；‎ ‎，．………………………………………………2分 ‎      （2） 因为第 组共有 人，…………………………3分 利用分层抽样在300 名员工中抽取6 人，每组抽取的人数分别为：‎ 第 1 组的人数为，…………………………………………………………4分 第 2 组的人数为， ………………………………………………………5分 第 3 组的人数为，‎ 所以第 组分别抽取1 人，1 人，4 人．………………………………………6分 ‎      （3） 由（2）可设第1 组的1 人为，第 2 组的 1 人为，第 3 组的 4 人分别为，则从 6 人中抽取 2 人的所有可能结果为：，，，，，，，，，，，，，，，共有 15 种．……………………………9分 其中 2 人年龄都不在第 3 组的有：，共 1 种；…………………………………11分 所以至少有 1 人年龄在第 3 组的概率为．……………………………12分 ‎22. 解：（1） 由题意知，圆心 坐标为，半径为2，‎ ‎①当切线斜率不存在时，直线方程为，满足题意；…………………………1分 ‎②当切线斜率存在时，设切线方程为：， ……………………………2分 所以，由，解得，‎ 所求的切线方程为 或．…………………………………………4分 ‎（2） 假设存在满足条件的实数，设，，‎ 联立 得， ……………………6分 因为，所以， ‎ 所以， ‎ 且， ……………………8分 因为，‎ 所以，……………………………………9分 又，…………………………………………10分 要使平行四边形为矩形，‎ 则，解得， …………………………11分 所以存在常数，使得平行四边形 为矩形．…………………………12分 另法：要使平行四边形为矩形，则，‎ 所以，即，‎ 所以，解得。‎